Plano de ensino – Análise no Rn I – 3q’25

Esta é a página sobre a disciplina MCTB004 – Análise no Rn I, ministrada no terceiro quadrimestre de 2025 para a seguinte turma:

A – Noturno, campus Santo André – horário: 3as. feiras 19h00-21h00, sala A-S008-0-SA e 5as. feiras 21h00-23h00, sala A-S305-1-SA.

Aqui encontram-se informações específicas sobre a turma acima.

Aulas

Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.

Aula 19 – 4.12.25 – Diferenciabilidade (ii): recapitulação – definição, diferencial de uma aplicação $m$ -dimensional, derivadas direcionais e sua linearidade como consequência de diferenciabildiade, derivadas parciais, diferenciabilidade implica continuidade, expressão da diferencial em componentes, matriz jacobiana de uma aplicação $m$ -dimensional e (vetor) gradiente de uma função num ponto, caracterização da diferenciabilidade de uma aplicação $m$ -dimensional em termos da diferenciabilidade de suas componentes e a relação entre as respectivas diferenciais. Regra da Cadeia para aplicações diferenciáveis: enunciado, prova e consequências (regras de cálculo diferencial para funções e aplicações diferenciáveis). Critério de diferenciabilidade de uma função em termos da continuidade das derivadas parciais, funções e aplicações (de classe) $C^1$ . 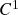Teorema da Função Inversa e Teorema da Função Implícita: enunciado. (Duistermaat-Kolk: Seções 2.2 a 2.4, 2.6, 3.2 e 3.5; Rudin: Seções 9.2, 9.4 e 9.5)
Aula 18 – 2.12.25 – Diferenciabilidade (i): definição, diferencial de uma aplicação $m$ -dimensional, motivação em termos da caracterização da existência da derivada de uma função de uma variável real em termos do Lema de Hadamard. Diferencial, derivadas direcionais e sua linearidade como consequência de diferenciabilidade, derivadas parciais. Diferenciabilidade implica continuidade, um contra-exemplo (uma função de duas variáveis reais descontínua na origem que possui todas as derivadas direcionais nesse ponto). Expressão da diferencial em componentes, matriz jacobiana de uma aplicação $m$ -dimensional e (vetor) gradiente de uma função num ponto. Caracterização da diferenciabilidade de uma aplicação $m$ -dimensional em termos da diferenciabilidade de suas componentes e a relação entre as respectivas diferenciais. Exemplos de aplicações diferenciáveis (i): aplicações constantes, lineares e bilineares. (Duistermaat-Kolk: Seções 2.1 a 2.3; Rudin: Seções 9.1 e 9.2)
Aula 17 – 27.11.25 – Limites e continuidade (v): sumário de resultados. Propriedades adicionais de limites e continuidade: limites de aplicações num ponto só dependem do comportamento da aplicação numa vizinhança arbitrariamente pequena desse ponto, comportamento de imagens de aplicações contínuas sob a operação de fecho. Caracterização sequencial de continuidade. Contrações em espaços métricos completos, Teorema de Ponto Fixo de Banach. (Duistermaat-Kolk: Seção 1.3; Elon: Seções I.7 e I.9; Rudin: Seções 4.1, 4.2 e 9.3)
Aula 16 – 25.11.25 – Limites e continuidade (iv): recapitulação – limite de uma aplicação entre (subconjuntos não-vazios de) espaços métricos num ponto de acumulação do domínio, aplicação contínuas num ponto, relação de continuidade com o conceito de limite num ponto de acumulação do domínio, continuidade automática em pontos isolados do domínio, comportamento de limites de funções a valores reais por operações algébricas (soma, produto, quociente). Limites de aplicações $m$ -dimensionais ( = a valores em 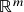$\mathbb{R}^m$ ) e de suas componentes. Limites compostos: condições para a validade da composição de limites e um contra-exemplo. Exemplos de aplicações contínuas (i): aplicações constantes e lipschitzianas, soma vetorial, multiplicação escalar e produto escalar em $\mathbb{R}^n$ . (Duistermaat-Kolk: Seção 1.3; Elon: Seções I.7 e I.9; Rudin: Seções 4.1 e 4.2)
Aula 15 – 18.11.25 – Limites e continuidade (iii): recapitulação – limite de uma aplicação entre (subconjuntos não-vazios de) espaços métricos num ponto de acumulação do domínio, aplicações contínuas num ponto, relação de continuidade com o conceito de limite num ponto de acumulação do domínio, continuidade automática em pontos isolados do domínio. Comportamento de limites de funções a valores reais com respeito a operações algébricas (soma, produto, quociente), compostas de aplicações contínuas são contínuas. (Duistermaat-Kolk: Seção 1.3; Elon: Seções I.7 e I.9; Rudin: Seções 4.1 e 4.2)
Aula 14 – 13.11.25 – Limites e continuidade (ii): recapitulação – limite de uma aplicação entre (subconjuntos não-vazios de) espaços métricos num ponto de acumulação do domínio, aplicação contínuas num ponto, relação de continuidade com o conceito de limite num ponto de acumulação do domínio, continuidade automática em pontos isolados do domínio. Aplicações uniformemente contínuas e Lipschitzianas, contrações e o Teorema de Ponto Fixo de Banach (enunciado). Consequências de continuidade de uma aplicação 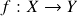$f:X\rightarrow Y$ entre espaços métricos 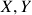$X,Y$ (i): 1.) caracterização global de continuidade (imagens inversas de abertos são abertas); 2.) imagens de compactos por aplicações contínuas são compactas ( 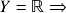$Y=\mathbb{R}\Rightarrow$ Teorema do Valor Extremo); 3.) imagens de conexos por aplicações contínuas são conexas ( 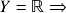$Y=\mathbb{R}\Rightarrow$ Teorema do Valor Intermediário); 4.) aplicações contínuas com domínio compacto são uniformemente contínuas (Teorema de Heine-Cantor). (Duistermaat-Kolk: Seção 1.3; Elon: Seções I.7 e I.9; Rudin: Seções 4.1 e 4.2)
Aula 13 – 11.11.25 – Conexidade (ii): recapitulação – definições básicas e propriedades. Subconjuntos entre um conexo e seu fecho são conexos, subconjuntos conexos com pelo menos dois pontos são perfeitos. Limites e continuidade (i): preliminares – imagens e imagens inversas de subconjuntos por funções: definição, comportamento por operações conjuntísticas (complementos, uniões e intersecções). Definições básicas – limite de uma função entre (subconjuntos não-vazios de) espaços métricos num ponto de acumulação do domínio, funções contínuas num ponto. Relação de continuidade com o conceito de limite num ponto de acumulação do domínio, continuidade automática em pontos isolados do domínio. (Duistermaat-Kolk: Seção 1.3; Elon: Seções I.7 e I.9; Rudin: Seções 4.1 e 4.2)
Aula 12 – 6.11.25 – Sequências em espaços métricos (ii): caracterização sequencial do fecho de um subconjunto de um espaço métrico (usando o Axioma da Escolha Enumerável), subespaços métricos de um espaço métrico completo são completos 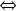$\Leftrightarrow$ são fechados. Conexidade (i): definições básicas – cisões triviais e não triviais de subconjuntos de um espaço métrico, subconjuntos conexos e desconexos. Propriedades de (des)conexidade – caracterizações intrínsecas em termos de uniões de pares de subconjuntos separados (não-vazios) e em termos da existência de subconjuntos (próprios) simultaneamente abertos e fechados ( = com fronteira vazia) na topologia relativa, caracterização dos intervalos de $\mathbb{R}$ como subconjuntos conexos, uniões de famílias de conexos com intersecção não-vazia são conexos. (Duistermaat-Kolk: Seção 1.9; Elon: Seção I.14; Rudin: Seções 3.3 e 2.5)
Aula 11 – 30.10.25 – Sequências em espaços métricos (i): preliminares – sequências, rearranjos e subsequências num conjunto. Sequências convergentes, sequências de Cauchy e sequências limitadas num espaço métrico – definição, limites de uma sequência convergente, propriedades (unicidade do limite de uma sequência convergente, convergente $\Rightarrow$ Cauchy $\Rightarrow$ limitada, sequências convergentes e sua subsequências possuem o mesmo limite, sequências de Cauchy com uma subsequência convergente converge para o mesmo limite), espaços métricos completos ( = toda sequência de Cauchy converge). Teorema de Bolzano-Weierstrass em espaços métricos (toda sequência com imagem contida num compacto possui uma subsequência convergente), espaços métricos com a propriedade de Heine-Borel (e.g. $\mathbb{R}^n$ ) são completos. (Rudin: Seções 3.1 a 3.3)
Aula 10 – 23.10.25 – Compacidade (iv): Teorema de Heine-Borel – conclusão da prova. Pontos de acumulação e pontos isolados de um subconjunto, subconjuntos perfeitos e discretos. Compacidade e propriedade de Bolzano-Weierstrass ( = todo subconjunto infinito possui ponto de acumulação). Interlúdio: axioma da escolha – versão geral, versão enumerável e axioma das escolhas dependentes. (Duistermaat-Kolk – seção 1.2; Elon – seção I.12; Rudin – seção 2.3)
Aula 9 – 21.10.25 – Compacidade (iii): recapitulação – definição de compacidade, propriedades de compacidade (iii) – subconjuntos finitos são compactos, compactos são limitados, compacidade é herdada por uniões e topologias relativas, compactos são fechados (relação com a propriedade de Hausdorff), subconjuntos fechados de compactos são compactos, famílias de compactos com a propriedade de intersecção finita. Lema dos compactos encaixantes. Propriedade de Heine-Borel ( = subconjuntos fechados e limitados são compactos): definição, prova no caso de $\mathbb{R}^n$ , redução ao caso de retângulos $n$ -dimensionais fechados (Teorema de Heine-Borel) – estratégia geral e resultados auxiliares (lema dos intervalos encaixantes e sua versão $n$ -dimensional). (Duistermaat-Kolk – seção 1.2; Elon – seção I.12; Rudin – seção 2.3)
Aula 8 – 16.10.25 – Compacidade (ii): recapitulação – preliminares (recobrimentos e subrecobrimentos de um subconjunto), definição de compacidade, propriedades de compacidade (ii) – subconjuntos finitos são compactos, compactos são limitados, compacidade é herdada por topologias relativas, compactos são fechados (relação com a propriedade de Hausdorff), subconjuntos fechados de compactos são compactos, famílias de compactos com a propriedade de intersecção finita. (Duistermaat-Kolk – seção 1.2; Elon – seção I.12; Rudin – seção 2.3)
Aula 7 – 14.10.25 – Topologia de espaços métricos (iv): subespaços métricos – definição (restrição da distância de um espaço métrico a um subconjunto não-vazio), caracterização da topologia de um subespaço métrico como topologia relativa induzida pel(a topologia d)o espaço métrico ambiente. Interlúdio: distâncias equivalentes induzem a mesma topologia. Compacidade (i): preliminares – recobrimentos e subrecobrimentos de um subconjunto, definição de compacidade, propriedades de compacidade (i) – subconjuntos finitos são compactos. (Duistermaat-Kolk – seção 1.2; Elon – seções I.4 e I.10 a I.12; Rudin – seções 2.2 e 2.3)
Aula 6 – 9.10.25 – Topologia de espaços métricos (iv): recapitulação – propriedades do interior e do fecho, bolas abertas (resp. bolas fechadas e esferas) num espaço métrico são abertas (resp. fechadas), o interior (resp. fecho) de um subconjunto é aberto (resp. fechado). Exemplos de abertos e fechados (iii): esferas em $\mathbb{R}^n$ munido da distância euclideana (e, mais em geral, em qualquer espaço vetorial normado) são a fronteira das bolas abertas e das bolas fechadas de mesmos raio e centro, semiespaços abertos (resp. semiespaços fechados e hiperplanos) em $\mathbb{R}^n$ munido da distância euclideana são abertos (resp. fechados), poliedros abertos (resp. fechados) em $\mathbb{R}^n$ são abertos (resp. fechados). Interior e fronteira de um poliedro fechado, o caso particular de retângulos $n$ -dimensionais. (Apostol – seção 8.2; Duistermaat-Kolk – seção 1.2; Elon – seções I.4, I.10 e I.11; Rudin – seção 2.2)
Aula 5 – 7.10.25 – Topologia de espaços métricos (iii): recapitulação – pontos interiores, exteriores, de fronteira e de aderência de um subconjunto, interior, exterior, fronteira e fecho de um subconjunto, subconjuntos abertos e fechados, axiomas de topologia para as famílias de abertos e fechados de um espaço métrico. Exemplos de abertos e fechados (ii): bolas abertas, bolas fechadas e esferas num espaço métrico, o interior (resp. fecho) de um subconjunto é aberto (resp. fechado), propriedades adicionais do interior e do fecho. (Apostol – seção 8.2; Duistermaat-Kolk – seção 1.2; Elon – seções I.4, I.10 e I.11; Rudin – seção 2.2)
Aula 4 – 2.10.25 – Topologia de espaços métricos (ii): recapitulação – pontos interiores, exteriores, de fronteira e de aderência de um subconjunto, interior, exterior, fronteira e fecho de um subconjunto, subconjuntos abertos e fechados. Axiomas de topologia para as famílias de abertos e fechados de um espaço métrico – enunciado e prova. Exemplos de abertos e fechados (i): bolas abertas, bolas fechadas e esferas num espaço métrico. O interior (resp. fecho) de um subconjunto é aberto (resp. fechado). (Apostol – seção 8.2; Duistermaat-Kolk – seções I.2, I.4, I.10 e I.11; Elon – seção I.4; Rudin – seção 2.2)
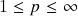Aula 3 – 30.9.25 – Espaços métricos: definição, axiomas de distância, exemplos – 1.) $\mathbb{R}^n$ munido da distância euclideana associada ao produto escalar canônico; 2.) espaços vetoriais (reais ou complexos) munidos da distância associada a uma norma, axiomas de norma. Equivalência de normas e distâncias: definição e exemplos – 1.) $p$ -normas em $\mathbb{R}^n$ , $1\leq p\leq\infty$ , 2.) normas num espaço vetorial (real ou complexo) de dimensão finita são equivalentes à norma euclideana associada a um produto escalar (prova parcial). Topologia de espaços métricos (i): pontos interiores, exteriores, de fronteira e de aderência de um subconjunto. Interior, exterior, fronteira e fecho de um subconjunto. Subconjuntos abertos e fechados. (Apostol – seções 8.1 e 8.2; Duistermaat-Kolk – seção 1.2; Elon – seções I.2, I.4, I.10 e I.11; Rudin – seção 2.2)
Aula 2 – 18.9.25 – Geometria (euclideana) de $\mathbb{R}^n$ (ii): recapitulação – definição de $\mathbb{R}^n$ , operações vetoriais e axiomas de espaço vetorial, produto escalar (canônico) e axiomas de produto escalar. Desigualdade de Cauchy -Schwarz: enunciado, prova e consequências – norma e distância euclideanas, axiomas de norma e distância, ângulo entre vetores não nulos (lei dos cossenos). (Apostol – Seções 1.2 a 1.4 e 1.11; Duistermaat-Kolk – Seção 1.1; Elon – Seções I.1 e I.2; Rudin – Seções 1.36 a 1.38)
Aula 1 – 16.9.25 – Informações sobre o funcionamento do curso. Geometria (euclideana) de $\mathbb{R}^n$ (i): operações vetoriais e axiomas de espaço vetorial, produto escalar (canônico) e axiomas de produto escalar, desigualdade de Cauchy-Schwarz (enunciado) e suas consequências – norma e distância euclideana, ângulo entre vetores não nulos (lei dos cossenos). (Apostol – Seções 1.2 a 1.4 e 1.11; Duistermaat-Kolk – Seção 1.1; Elon – Seções I.1 e I.2; Rudin – Seções 1.36 a 1.38)

Bibliografia

Listamos aqui os textos que seguiremos mais de perto.

Johannes J. Duistermaat, Johan A.C. Kolk, Multidimensional Real Analysis I – Differentiation. Cambridge University Press, 2004;
Elon L. Lima, Curso de Análise – Volume 2 (11a. edição). Projeto Euclides, IMPA, 2009;
Walter Rudin, Principles of Mathematical Analysis (3a. edição). McGraw-Hill, 1976;
Robert S. Strichartz, The Way of Analysis (ed. revisada). Jones and Bartlett, 2000;
Terence Tao, Analysis II (3a. edição). Hindustan Book Agency, 2014.

Textos suplementares:

Tom M. Apostol, Cálculo, Volume 2 (segunda edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969);
Robert G. Bartle, The Elements of Real Analysis (segunda edição). Wiley, 1976;
Chaim S. Hönig, Aplicações da Topologia à Análise. Editora Livraria da Física, 2011;
Elon L. Lima, Análise no Espaço $\mathbb{R}^n$ (segunda edição). Coleção Matemática Universitária, IMPA, 2010.

Recomendações e material didático suplementar

É recomendado que o aluno tenha cursado anteriormente as disciplinas MCTB001 – Álgebra Linear e MCBM002 – Análise Real I, pois vários tópicos destas serão abordados de maneira mais breve ou simplesmente usados de maneira tácita. Indicamos material encontrado em algumas das referências acima para o aluno que sentir necessidade de revisar de maneira mais profunda conceitos vistos nesses cursos.

MCTB001 – Álgebra Linear: Apostol – capítulos 1 a 5
MCBM002 – Análise Real I: Rudin – capítulos 1, 4 e 5; Strichartz – capítulos 2 a 5

Avaliação

Média preliminar:
M_p = 0,5*(P₁+P₂)
Média final:
M_p = 0,5*max(P₁+P₂, Rec+P₁, Rec+P₂)
Critério de conversão de média preliminar (M_p) / final (M_f) para conceito preliminar (C_p) / final (C_f): C_p (resp. C_f) = F – M_p (resp. M_f) < 4,5;
C_p (resp. C_f) = D – M_p (resp. M_f) = 4,5-5,2;
C_p (resp. C_f) = C – M_p (resp. M_f) = 5,3-6,9;
C_p (resp. C_f) = B – M_p (resp. M_f) = 7,0-8,4;
C_p (resp. Cf) = A – M_p (resp. M_f) = 8,5-10,0.
Haverá uma prova substitutiva e uma prova de recuperação no final do curso. O conteúdo de ambas as provas compreenderá toda a matéria.
A prova substitutiva só poderá ser feita por participantes que não puderem comparecer a uma das provas, com justificativa formal por escrito da ausência entregue ao docente no máximo até o horário de início da prova substitutiva. Preferencialmente o documento físico original e/ou digital com assinatura digital deve ser entregue; se não por possível (e.g. pelo documento original ser exigido para justificar ausência em provas de outras disciplinas), será aceita uma cópia digitalizada enviada por email mas será exigido nesse caso que @ participante apresente o documento original para conferência dentro do mesmo prazo.
A prova de recuperação será aplicada no início do 1q’26, em data e local a serem divulgados futuramente. Apenas participantes que ficaram com conceitos preliminares D e F (ver critério acima) após a aplicação da prova substitutiva poderão fazer essa prova.
Datas das provas:
P1 – 4.11 (terça-feira);
P2 – 9.12 (terça-feira);
Sub – 11.12 (quinta-feira, se houver necessidade);
Rec – início do primeiro quadrimestre de 2026, a divulgar.

Listas de exercícios

É extremamente importante que @s participantes façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!

@s participantes que assim desejarem poderão entregar as suas resoluções das listas correspondentes à matéria de cada prova até a aula seguinte a prova correspondente (P1 – 6.11; P2 – data da Rec). Tais listas serão avaliadas nos casos de média final limítrofe para aprovação (ver tabela de conversão de conceitos acima), convertendo-se num bônus de até 1,5 ponto na média final.

Plantão de dúvidas

Haverá um plantão de dúvidas às segundas-feiras das 17h00 às 19h00, na minha sala (A-S543-2, Torre 2, Bloco A, campus Santo André). O plantão terá início no dia 22.9.

Roteiro

Abaixo indicamos brevemente a ordem de tópicos a ser seguida, com indicações das seções correspondentes nos três livros-texto principais listados acima. Esse roteiro poderá sofrer ligeiras modificações e/ou omissões ao longo do curso, na medida do necessário.

Notar que essas seções podem ocasionalmente conter mais material do que será visto em aula – um guia mais preciso do conteúdo será dado pelos exercícios das listas (e, é claro, pelo material apresentado em aula 😉 ).

$\mathbb{R}^n$ como espaço vetorial e como espaço métrico: produto escalar, projeções ortogonais, norma Euclideana e distância Euclideana (Duistermaat-Kolk – seção 1.1; Elon – seções I.1 e I.2; Rudin – seções 1.36 a 1.38);
Topologia de $\mathbb{R}^n$ : pontos de aderência e pontos interiores, abertos e fechados, fecho, interior e fronteira, subconjuntos limitados, pontos de acumulação e pontos isolados, subconjuntos conexos, subconjuntos perfeitos e discretos (Duistermaat-Kolk – seções 1.2, 1.6, 1.8 e 1.9; Elon – seções I.4, I.6, I.10, I.11 e I.14; Rudin – seções 2.15 a 2.30 e 2.43 a 2.47);
Sequências em $\mathbb{R}^n$ : limites e subsequências, sequências limitadas e de Cauchy, completeza de $\mathbb{R}^n$ (Duistermaat-Kolk – seções 1.1 e 1.6; Elon – seção 1.5; Rudin – seções 3.1 a 3.12);
Recobrimentos e compacidade: subconjuntos compactos, o teorema de Heine-Borel-Lebesgue em $\mathbb{R}^n$ (Duistermaat-Kolk – seção 1.8; Elon – seção I.12; Rudin – seções 2.31 a 2.42);
Funções e aplicações em abertos de $\mathbb{R}^n$ e seus limites (Duistermaat-Kolk – seção 1.3; Elon – seção I.9; Rudin – seções 2.1, 2.2 e 4.1 a 4.4);
Aplicações contínuas: formulação local e global, preservação de operações algébricas e de composição, continuidade da inversa e homeomorfismos, aplicações Lipschitzianas, contrações e o teorema de ponto fixo de Banach, preservação de conexidade e compacidade por aplicações contínuas (Duistermaat-Kolk – seções 1.3 a 1.5, e 1.7 a 1.9; Elon – seções I.7, I.8 a I.12, e I.14; Rudin – seção 4.5 a 4.23, 9.22 e 9.23);
Aplicações diferenciáveis: derivada direcional e diferencial de uma aplicação, derivadas parciais, aplicações diferenciáveis e continuamente diferenciáveis, a matriz Jacobiana, linearidade da diferenciação, regra da cadeia (Duistermaat-Kolk – seções 2.1 a 2.6; Elon – seções III.1 a III.6, e V.1 a V.3; Rudin – seções 9.10 a 9.21);
Diferenciação de funções de várias variáveis em ordem superior: a matriz Hessiana, critério de comutatividade de derivadas parciais (teorema de Schwarz), fórmula de Faà di Bruno, fórmula de Taylor para funções de várias variáveis (Duistermaat-Kolk – seções 2.7 e 2.8; Elon – seções III.7, III.8 e V.4; Rudin – seções 9.39 a 9.41);
Máximos e mínimos de funções diferenciáveis, funções convexas (Duistermaat-Kolk – seção 2.9);
Difeomorfismos e o Teorema da Aplicação Inversa (Duistermaat-Kolk – seções 3.1 a 3.3; Elon – seção V.8; Rudin – seção 9.24 e 9.25);
Aplicações implícitas e o Teorema da Aplicação Implícita (Duistermaat-Kolk – seções 3.4 a 3.6; Elon – seções III.9 e V.8; Rudin – seções 9.26 e 9.29);
Hipersuperfícies: formulação paramétrica, gráfica e implícita, multiplicadores de Lagrange, subvariedades de $\mathbb{R}^n$ (Duistermaat-Kolk – seções 4.1, 4.2, 5.4 e 5.5; Elon – seções III.10, e V.10 a V.15; Rudin – seções 9.30 a 9.32).