Este é o plano de ensino para a disciplina de pós-graduação MAT-244 – Teorias de Gauge e Fibrados conforme ministrada no primeiro quadrimestre letivo de 2024.
Horário presencial: 2as. feiras 14h00-16h00 e 4as. feiras 16h00-18h00, sala A-S311-2.
Novidades
Notícias recentes sobre o funcionamento do curso serão disponibilizadas aqui.
Aulas
Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.
- Aula 20 – 22.4.24 – Integração de formas diferenciais (ii): a integral de uma
 -forma diferencial com suporte compacto num aberto de uma variedade suave
-forma diferencial com suporte compacto num aberto de uma variedade suave  -dimensional orientada – o caso de domínios de cartas orientadas com a mesma orientação, independência da escolha de carta (mudança de variáveis em termos de “pullbacks”), o caso geral em termos de partições de unidade. A integral de uma
-dimensional orientada – o caso de domínios de cartas orientadas com a mesma orientação, independência da escolha de carta (mudança de variáveis em termos de “pullbacks”), o caso geral em termos de partições de unidade. A integral de uma 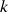 -forma diferencial com suporte compacto numa subvariedade orientada de dimensão
-forma diferencial com suporte compacto numa subvariedade orientada de dimensão 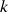 usando o “pullback” pela inclusão natural. O teorema de Stokes para
usando o “pullback” pela inclusão natural. O teorema de Stokes para 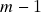 formas com suporte compacto – enunciado e prova, comentários sobre o caso de
formas com suporte compacto – enunciado e prova, comentários sobre o caso de 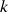 -formas para
-formas para 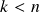 .
. - Aula 19 – 17.4.24 – Integração de formas diferenciais (i): preliminares – atlas orientados e orientações nuam variedade suave, variedades orientáveis e orientadas. Caracterização de orientabilidade de uma variedade suave
 -dimensional
-dimensional 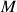 pela existência de uma
pela existência de uma  -forma diferencial que não se anula em parte alguma.
-forma diferencial que não se anula em parte alguma. - Aula 18 – 15.4.24 – Formas diferenciais (iii): derivada exterior de formas diferenciais (ii) – recapitulação (fórmula explícita, propriedades da derivada exterior – 1.) linearidade, 2.) regra de Leibniz graduada com respeito ao produto exterior, 3.) comutatividade com “pullbacks” e 4.) nilpotência). Prova da comutatividade da derivada exterior com “pullbacks” (i).
- Aula 17 – 10.4.24 – Formas diferenciais (ii): derivada exterior de formas diferenciais (ii) – recapitulação (definição recursiva em termos da derivada de Lie, fórmula de H. Cartan), fórmula explícita. Propriedades da derivada exterior: 1.) linearidade, 2.) nilpotência, 3.) regra de Leibniz graduada com respeito ao produto exterior e 4.) comutatividade com “pullbacks”.
- Aula 16 – 3.4.24 – Formas diferenciais (i): definição, estrutura de
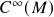 -módulo. “Pullback” de campos tensoriais covariantes e de formas diferenciais por aplicações suaves – definição, o caso particular de inclusões de subvariedades (restrição a subvariedades), forma local de formas diferenciais e seu “pullback” no domínio de uma carta, comutação com o produto exterior. Derivada exterior de formas diferenciais (i) – definição recursiva em termos da derivada de Lie (fórmula de H. Cartan), forma local no domínio de uma carta.
-módulo. “Pullback” de campos tensoriais covariantes e de formas diferenciais por aplicações suaves – definição, o caso particular de inclusões de subvariedades (restrição a subvariedades), forma local de formas diferenciais e seu “pullback” no domínio de uma carta, comutação com o produto exterior. Derivada exterior de formas diferenciais (i) – definição recursiva em termos da derivada de Lie (fórmula de H. Cartan), forma local no domínio de uma carta. - Aula 15 – 1.4.23 – Campos tensoriais (iii): projeções lineares de simetrização e anti-simetrização de argumentos tensoriais – definição e propriedades, comutação com potências tensoriais de transformações lineares invertíveis. Subfibrados vetoriais de tensores com subconjuntos de entradas (anti-)simétricas, tensores contravariantes e covariantes (anti-)simétricos de posto
 ( =
( =  -vetores e
-vetores e  -formas). Produto exterior.
-formas). Produto exterior. - Aula 14 – 27.3.24 – Campos tensoriais (ii): derivada de Lie
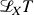 de um campo tensorial
de um campo tensorial 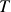 ao longo de um campo vetorial
ao longo de um campo vetorial 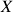 numa variedade
numa variedade 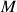 – definição em termos do fluxo de
– definição em termos do fluxo de 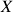 e definição algébrica, casos particulares (
e definição algébrica, casos particulares (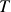 escalar: derivada usual;
escalar: derivada usual; 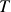 vetorial: colchete de Lie). Propriedades da derivada de Lie – bilinearidade, violação de
vetorial: colchete de Lie). Propriedades da derivada de Lie – bilinearidade, violação de 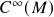 -linearidade, comutador de derivadas de Lie (
-linearidade, comutador de derivadas de Lie (  identidade de Jacobi para o colchete de Lie), regra de Leibniz com respeito a contrações tensoriais e produto tensorial, colchete de Lie de campos vetoriais
identidade de Jacobi para o colchete de Lie), regra de Leibniz com respeito a contrações tensoriais e produto tensorial, colchete de Lie de campos vetoriais  -relacionados para
-relacionados para  aplicação suave. Subfibrados vetoriais de posto
aplicação suave. Subfibrados vetoriais de posto 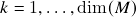 do fibrado tangente, subfibrados vetoriais involutivos e o teorema de Frobenius: enunciado, folheação integral e folhas ( = subvariedades) integrais (maximais) de um subfibrado vetorial involutivo do fibrado tangente, fluxo maximal de um campo vetorial como caso particular (posto 1).
do fibrado tangente, subfibrados vetoriais involutivos e o teorema de Frobenius: enunciado, folheação integral e folhas ( = subvariedades) integrais (maximais) de um subfibrado vetorial involutivo do fibrado tangente, fluxo maximal de um campo vetorial como caso particular (posto 1). - Aula 13 – 25.3.24 – Campos tensoriais (i): campos vetoriais como seções suaves do fibrado tangente, campos tensoriais de posto contravariante
 e posto covariante
e posto covariante 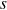 = campos
= campos 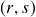 -tensoriais como seções suaves do fibrado
-tensoriais como seções suaves do fibrado 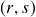 -tensorial de
-tensorial de 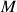 . Caracterização algébrica de campos
. Caracterização algébrica de campos 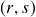 -tensoriais.
-tensoriais. - Aula 12 – 20.3.24 – Campos vetoriais (ii): recapitulação – definição em termos de campos suaves de derivações pontuais e derivações na álgebra de funções suaves. O fluxo de um campo vetorial: domínios de fluxo, fluxos e geradores – definição. Campos vetoriais como equações diferenciais ordinárias: curvas integrais e fluxo (maximal) gerado por um campo vetorial. Colchete de Lie de campos vetoriais (i): definição e propriedades algébricas (i) – linearidade e regra de Leibniz, o colchete de Lie como uma derivada de Lie.
- Aula 11 – 18.3.24 – Campos vetoriais (i): definição em termos de campos suaves de derivações pontuais e derivações na álgebra de funções suaves, equivalência entre as duas definições. O suporte de um campo vetorial. Restrição de campos vetoriais a abertos, extensão por zero de campos vetoriais com suporte compacto. O
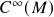 -módulo dos campos vetoriais numa variedade suave
-módulo dos campos vetoriais numa variedade suave 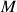 , bases locais de campos vetoriais induzida por uma carta. Colagem de campos vetoriais locais no recobrimento localmente finito associado a um atlas de
, bases locais de campos vetoriais induzida por uma carta. Colagem de campos vetoriais locais no recobrimento localmente finito associado a um atlas de 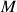 : partições de unidade, o papel da paracompacidade de
: partições de unidade, o papel da paracompacidade de 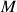 .
. - Aula 10 – 13.3.24 – Interlúdio – produtos tensoriais (ii). Variedades suaves (x): vetores tangentes (vii) – espaços de tensores tangentes a um ponto com posto contravariante
 e post covariante
e post covariante 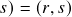 -tensores tangentes a um ponto. O fibrado de
-tensores tangentes a um ponto. O fibrado de 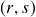 -tensores numa variedade suave: estrutura suave e estrutura de fibrado vetorial induzida por um atlas da base.
-tensores numa variedade suave: estrutura suave e estrutura de fibrado vetorial induzida por um atlas da base. - Aula 9 – 11.3.24 – Variedades suaves (ix): vetores tangentes (vi) – Estrutura de variedade suave e de fibrado vetorial dos fibrados tangente e cotangente induzida por um atlas da base. Interlúdio – produtos tensoriais (i).
- Aula 8 – 6.3.24 – Variedades suaves (viii): vetores tangentes (v) – aplicação tangente ( = diferencial) de uma aplicação suave num ponto do domínio, expressão em termos da matriz jacobiana num par de cartas no domínio e no contradomínio (recapitulação), forma invariante da regra da cadeia. A diferencial de uma função suave num ponto, espaço cotangente. Estrutura de variedade suave e de fibrado vetorial do fibrado tangente induzida por um atlas da base.
- Aula 7 – 4.3.24 – Variedades suaves (vii): vetores tangentes (iv) – base de vetores tangentes cinemáticos do espaço tangente a um ponto gerada por uma carta. Aplicação tangente ( = diferencial) de uma aplicação suave num ponto do domínio, expressão em termos da matriz jacobiana num par de cartas no domínio e no contradomínio. Imersões e submersões: definição, forma local em termos do Teorema da Função Inversa e do Teorema da Função Implícita, subvariedades imersas.
- Aula 6 – 28.2.24 – Variedades suaves (vi): vetores tangentes (iii) – recapitulação (álgebra de funções suaves numa variedade suave, álgebra de funções suaves numa vizinhança aberta de um ponto numa variedade suave). Localidade de derivações pontuais (ii): funções solavanco suaves em variedades suaves e o papel da propriedade de Hausdorff, funções suaves que coincidem numa vizinhança de um ponto tem o mesmo valor para qualquer derivação pontual nesse ponto, lema de Hadamard ( <= Teorema Fundamental do Cálculo) e base de vetores tangentes cinemáticos no espaço tangente.
- Aula 5 – 26.2.24 – Variedades suaves (v): vetores tangentes (ii) – recapitulação (definição cinemática = derivada direcional ao longo de uma curva suave num ponto, definição operacional = derivação pontual). Álgebra de funções suaves numa variedade suave, álgebra de funções suaves numa vizinhança aberta de um ponto numa variedade suave. Propriedades de derivações pontuais. Localidade de derivações pontuais: funções solavanco suaves em abertos ao redor de um ponto – construção em
 , extensão suave por zero, construção para variedades suaves e o papel da propriedade de Hausdorff.
, extensão suave por zero, construção para variedades suaves e o papel da propriedade de Hausdorff. - Aula 4 – 21.2.24 – Variedades suaves (iv): subvariedades
 -dimensionais de uma variedade suave
-dimensionais de uma variedade suave  -dimensional (
-dimensional (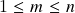 ): definição, casos extremos
): definição, casos extremos 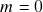 (subconjuntos discretos) e
(subconjuntos discretos) e 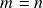 (subconjuntos abertos), cartas adaptadas a uma subvariedade
(subconjuntos abertos), cartas adaptadas a uma subvariedade  -dimensional, estrutura suave
-dimensional, estrutura suave  -dimensional numa subvariedade
-dimensional numa subvariedade  -dimensional (
-dimensional (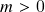 ), teorema de Whitney (enunciado). Aplicações suaves (ii): definição (recapitulação), difeomorfismos e mergulhos, subvariedades mergulhadas, reformulação do teorema de Whitney em termos de subvariedades mergulhadas. Casos particulares de aplicações suaves: 1.) funções suaves numa variedade suave (contradomínio =
), teorema de Whitney (enunciado). Aplicações suaves (ii): definição (recapitulação), difeomorfismos e mergulhos, subvariedades mergulhadas, reformulação do teorema de Whitney em termos de subvariedades mergulhadas. Casos particulares de aplicações suaves: 1.) funções suaves numa variedade suave (contradomínio =  ), 2.) curvas suaves numa variedade suave (domínio = intervalo aberto de
), 2.) curvas suaves numa variedade suave (domínio = intervalo aberto de  ). Vetores tangentes (i): definição cinemática (derivada direcional ao longo de uma curva suave num ponto) e definição operacional (derivações pontuais).
). Vetores tangentes (i): definição cinemática (derivada direcional ao longo de uma curva suave num ponto) e definição operacional (derivações pontuais). - Aula 3 – 19.2.24 – Variedades suaves (iii): recapitulação – cartas (locais)
 -dimensionais e atlas
-dimensionais e atlas  -dimensionais suaves num conjunto, compatibiliidade de cartas
-dimensionais suaves num conjunto, compatibiliidade de cartas  -dimensionais com um atlas
-dimensionais com um atlas  -dimensional suave, compatibilidade entre atlas
-dimensional suave, compatibilidade entre atlas  -dimensionais suaves, atlas
-dimensionais suaves, atlas  -dimensional suave maximal gerado por um atlas
-dimensional suave maximal gerado por um atlas  -dimensional suave, estruturas suaves
-dimensional suave, estruturas suaves  -dimensionais, a topologia induzida por um atlas
-dimensionais, a topologia induzida por um atlas  -dimensional suave. Continuidade de aplicações com respeito à topologia de uma variedade suave. Aplicações suaves (i): definição, independência do representante da classe de equivalência do atlas por compatibilidade. Casos particulares de aplicações suaves: 1.) funções suaves numa variedade suave (contradomínio =
-dimensional suave. Continuidade de aplicações com respeito à topologia de uma variedade suave. Aplicações suaves (i): definição, independência do representante da classe de equivalência do atlas por compatibilidade. Casos particulares de aplicações suaves: 1.) funções suaves numa variedade suave (contradomínio =  ), 2.) curvas suaves numa variedade suave (domínio = intervalo aberto de
), 2.) curvas suaves numa variedade suave (domínio = intervalo aberto de  ).
). - Aula 2 – 7.2.24 – Variedades suaves (ii): recapitulação – cartas (locais)
 -dimensionais e atlas
-dimensionais e atlas  -dimensionais suaves num conjunto, compatibiliidade de cartas
-dimensionais suaves num conjunto, compatibiliidade de cartas  -dimensionais com um atlas
-dimensionais com um atlas  -dimensional suave, compatibilidade entre atlas
-dimensional suave, compatibilidade entre atlas  -dimensionais suaves, atlas
-dimensionais suaves, atlas  -dimensional suave maximal gerado por um atlas
-dimensional suave maximal gerado por um atlas  -dimensional suave, estruturas suaves
-dimensional suave, estruturas suaves  -dimensionais. Exemplos: 1.) abertos de
-dimensionais. Exemplos: 1.) abertos de  (atlas unitário contendo a identidade), 2.) esferas
(atlas unitário contendo a identidade), 2.) esferas  -dimensionais (projeções estereográficas nos polos). A topologia induzida por um atlas
-dimensionais (projeções estereográficas nos polos). A topologia induzida por um atlas  -dimensional suave – definição, independência do representante da classe de equivalência do atlas por compatibilidade e propriedades desejáveis (propriedade de Hausdorff, paracompacidade).
-dimensional suave – definição, independência do representante da classe de equivalência do atlas por compatibilidade e propriedades desejáveis (propriedade de Hausdorff, paracompacidade). - Aula 1 – 5.2.24 – Informações sobre o funcionamento do curso. Motivação: o que são teorias de calibre, e qual a linguagem matemática usada para descrevê-las? Variedades suaves (i): cartas (locais)
 -dimensionais e atlas
-dimensionais e atlas  -dimensionais suaves num conjunto, compatibiliidade de cartas
-dimensionais suaves num conjunto, compatibiliidade de cartas  -dimensionais com um atlas
-dimensionais com um atlas  -dimensional suave, compatibilidade entre atlas
-dimensional suave, compatibilidade entre atlas  -dimensionais suaves. O atlas
-dimensionais suaves. O atlas  -dimensional suave maximal gerado por um atlas
-dimensional suave maximal gerado por um atlas  -dimensional suave, estruturas suaves
-dimensional suave, estruturas suaves  -dimensionais.
-dimensionais.
Bibliografia
Listamos aqui os textos que seguiremos mais de perto.
- D. Bleecker, Gauge Theory and Variational Principles (Dover, 1981).
- R. Bott, L. W. Tu, Differential Forms in Algebraic Topology (Springer-Verlag, 1982).
- M. J. D. Hamilton, Mathematical Gauge Theory With Applications to the Standard Model of Particle Physics (Springer, 2017).
- N. J. Hicks, Notes on Differential Geometry (Van Nostrand Reinhold, 1965). Edição digital revisada pelo grupo
 do fórum online Discord (2022).
do fórum online Discord (2022). - S. Kobayashi, K. Nomizu, Foundations of Differential Geometry, Volume I (Wiley, 1963), Volume II (Wiley, 1969).
- I. Kolář, P. W. Michor, J. Slovák, Natural Operations in Differential Geometry (Springer-Verlag, 1993). Disponível online na homepage do autor.
- J. M. Lee, Manifolds and Differential Geometry (American Mathematical Society, 2009).
- J. M. Lee, Introduction to Smooth Manifolds (Springer-Verlag, 2002).
- P. W. Michor, Topics in Differential Geometry (American Mathematical Society, 2008).
- L. W. Tu, Introduction to Manifolds (2a. edição, Springer-Verlag, 2011).
- L. W. Tu, Differential Geometry: Connections, Curvature, and Characteristic Classes (Springer-Verlag, 2017).
- Notas de aula serão disponibilizadas aqui à medida que o conteúdo for apresentado.
Textos suplementares:
- J. C. Baez, J. P. Muniain, Gauge Fields, Knots and Gravity (World Scientific, 1994).
- E. Binz, J. Śniatycki, H. Fischer, Geometry of Classical Fields (North-Holland, 1988).
- M. Forger, H. Römer, Currents and the Energy-Momentum Tensor in Classical Field Theory: a Fresh Look at an Old Problem. Ann. Phys. 309 (2004) 306–389, arXiv:hep-th/0307199.
- G. Mack, Physical Principles, Geometrical Aspects, and Locality Properties of Gauge Field Theories. Fortschr. Phys. 29 (1981) 135–185.
- M. Nakahara, Topology, Geometry and Physics (2a. edição, IoP Publishing, 2003).
- V. Rubakov, Classical Theory of Gauge Fields (Princeton University Press, 2002).
- L. H. Ryder, Quantum Field Theory (2a. edição, Cambridge University Press, 1996).
- P. Szekeres, A Course in Modern Mathematical Physics – Groups, Hilbert Space and Differential Geometry (Cambridge University Press, 2004).
Recomendações e material didático suplementar
Faremos uso de tópicos apresentados na disciplina de doutorado MAT-266 – Variedades Diferenciáveis, mas ter cursado previamente essa disciplina não é indispensável já que os conceitos necessários serão introduzidos conforme o andamento do curso exigir, ainda que de maneira sucinta. Não é necessário conhecimento prévio de Teoria de Campos, mas tal conhecimento certamente ajuda a motivar a disciplina.
Objetivos
Nosso objetivo aqui é apresentar os fundamentos conceituais da classe de teorias clássicas de campos conhecidas como teorias de gauge ou teorias de calibre, que descrevem três das quatro interações fundamentais entre partículas elementares – a saber, as interações eletromagnética, fraca e forte. A linguagem matemática que descreve a cinemática de tais teorias de campos é dada pelo formalismo de fibrados e conexões sobre a variedade espaço-temporal, o qual será apresentado em detalhes. A dinâmica destas, por sua vez, é determinada por um princípio variacional aplicado a uma família de funcionais conjuntamente denominada ação. A extremização da ação leva às equações de movimento (de Euler-Lagrange) para os campos. Teorias de gauge possuem uma família de simetrias locais conhecidas como transformações de gauge ou transformações de calibre, e a invariância da ação por tais simetrias leva a leis de conservação por meio do chamado Teorema de Noether. As quantidades conservadas por tais leis estão ligadas a quantidades fisicamente observáveis que também podem possuir uma interpretação matemática em termos de invariantes topológicos. Desta forma, o estudo das teorias (clássicas) de calibre é de interesse fundamental tanto em Física como em Matemática.
Avaliação
A diferença entre os dois tipos de tópicos, listados abaixo, é a seguinte: os tópicos básicos serão apresentados nas auals expositivas e servirão como base para os tópicos especiais, que na verdade constituem uma lista aberta de tópicos de livre escolha para os seminários de avaliação, a serem apresentados pel@s alun@s no final do curso (datas a serem agendadas entre 29.4 e 7.5). O conceito final é baseado nesses seminários e na participação d@s alun@s, a última tanto nas aulas como nos seminários d@s colegas.
É recomendada a consulta à bibliografia listada acima para mais detalhes e ideias de tópicos para os seminários de avaliação.
Dúvidas
Será mantido um fórum de dúvidas permanente e aberto para discussões e dúvidas sobre o conteúdo da disciplina. Os alunos são livres (e encorajados!) para fazer perguntas e também responder às dúvidas dos colegas. Em virtude do número reduzido de participantes, plantões de dúvidas por videoconferência no Google Meet poderão ser agendados pontualmente se necessário.
Roteiro
Será varrido essencialmente o conteúdo da ementa oficial da disciplina, disponível na página da Posmat, mas com modificações na ordem e ênfase dos tópicos. O conteúdo do curso será dividido em duas partes:
- (a) Tópicos básicos
• Variedades, aplicações diferenciáveis e campos vetoriais. O fluxo de um campo vetorial, colchete de Lie.
• Formas diferenciais, derivada exterior e o teorema de Stokes. Cohomologia de de Rham.
• Grupos de Lie, álgebras de Lie e espaços homogêneos.
• Fibrados gerais, conexões e curvatura. Morfismos de fibrados e transformações de calibre. Fibrados vetoriais, fibrados principais e fibrados associados. Redução de grupo estrutural de um fibrado principal, campos de Higgs.
• Conexões lineares, conexões principais e induzidas, campos de calibre. Derivada covariante. Transporte paralelo e holonomia de uma conexão.
• Funcionais ação e lagrangeanas, princípio variacional e equações de Euler-Lagrange. Simetrias e o Teorema de Noether. Campos de Yang-Mills. - (b) Tópicos especiais
• Campos de matéria: estruturas de spin, fibrados espinoriais e campos de Dirac. Acoplamento mínimo com campos de calibre, quarks e léptons.
• Quebra espontânea de simetria de calibre e mecanismo de Higgs. O Modelo Padrão.
• Manifestações físicas da holonomia de um campo de calibre: o efeito Aharonov-Bohm.
• Conexões e classes características: monopolos e ínstantons.
• Tópico livre a ser proposto pel@s alun@s em comum acordo com o docente dentro do contexto da disciplina.

