Esta é a página sobre a disciplina BCN0402 – Funções de Uma Variável, ministrada no primeiro quadrimestre de 2024 para as seguintes turmas:
- A1 – Noturno, campus Santo André – horário: 2as. feiras 19h00-21h00 e 4as. feiras 21h00-23h00, sala A-S008-0-SA.
- B1 – Noturno, campus Santo André – horário: 2as. feiras 21h00-23h00 e 4as. feiras 19h00-21h00, sala A-S106-0-SA.
Aqui encontram-se informações específicas sobre as turmas acima – informações gerais sobre o curso podem ser encontradas na página do Gradmat para a disciplina de FUV.
Novidades
Notícias recentes sobre o funcionamento do curso serão disponibilizadas aqui.
Aulas
Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.
- Aula 19 – 22.4.24 – Aplicações de cálculo integral (iv): 3.) valor médio de uma função – derivação a partir de somas de Riemann, relação com o Teorema do Valor Médio. 4.) Centro de massa ( = centroide = baricentro) de uma região plana – derivação a partir de somas de Riemann, relação com o volume de um sólido de revolução (teorema de Pappus). 5.) Comprimento de carco do gráfico de uma função – definição a partir de somas de Riemann, exemplos (comprimento de arco de um trecho de um círculo e relação com a área do setor circular correspondente sem o uso de funções trigonométricas).
- Aula 18 – 17.4.24 – Aplicações de cálculo integral (iii): recapitulação – teorema fundamental do Cálculo, área entre os gráficos de duas funções contínuas (derivação a partir de somas de Riemann), volumes de sólidos (princípio de Cavalieri e exemplos de sua aplicação). Volumes de sólidos de revolução ao redor do eixo horizontal (“método dos discos”) e ao redor do eixo vertical (“método das cascas cilíndricas”).
- Aula 16 – 10.4.24 – A integral de Riemann (ii): recapitulação – Integral de Riemann superior e inferior, funções integráveis e integral de Riemann. Propriedades da integral de Riemann: 1.) linearidade, 2.) positividade e 3.) aditividade. O teorema fundamental do Cálculo (enunciado) – funções contínuas são integráveis e, nesse caso, a integral de Riemann coincide com a integral definida. Aplicações de cálculo integral (i): área entre os gráficos de duas funções contínuas.
- Aula 15 – 3.4.24 – Primitivas (ii): recapitulação – definição formal, notação e propriedades – diferença entre duas primitivas de uma mesma função é constante, integrais indefinidas, especificação da constante arbitrária, integrais definidas, regras de primitivação (1.) linearidade 2.) integração por partes, 3.) integração por substituição). Exemplos de cálculo de integrais indefinidas. A integral de Riemann (i): preliminares – área com sinal entre o gráfico de uma função e um intervalo, partições e somas de Riemann superiores / inferiores de uma função limitada com respeito a uma partição, interpretação geométrica, amostras de uma partição e soma de Riemann com respeito a uma partição com amostra. Refinamento de partições e seu efeito sobre somas de Riemann superiores / inferiores (método de exaustão). Integral de Riemann superior e inferior, funções integráveis e integral de Riemann.
- Aula 14 – 1.4.24 – Primitivas (i): definição formal, notação e propriedades – diferença entre duas primitivas de uma mesma função é constante, integrais indefinidas, especificação da constante arbitrária, integrais definidas. Interpretação cinemática: recuperando a posição de uma trajetória a partir de sua velocidade e uma posição inicial. Regras de primitivação: 1.) linearidade 2.) integração por partes, 3.) integração por substituição. Propriedades adicionais de integrais definidas com respeito aos extremos de integração, integrais definidas de funções não-negativas são não-negativas. Exemplos de cálculo de integrais indefinidas (i): regra do tombo inversa, funções exponenciais.
- Aula 13 – 25.3.24 – Problemas de otimização: roteiro – 1.) modelagem matemática do problema concreto (identificação das variáveis e suas relações entre si, formulação do problema como determinação de máximos e mínimos de uma função no domínio relevante para o problema); 2.) solução do problema matemático abstrato obtido no passo 1.); 3.) interpretação da solução no contexto do problema original. Erro da aproximação de uma função por polinômios de Taylor: Teorema do Valor Médio de ordem
 , estimativa do erro de aproximação. Formas indeterminadas e regra de l’Hôspital: enunciado da regra, cuidados necessários à sua aplicação ao cálculo de limites (checar se a expressão no limite é uma forma indeterminada do tipo
, estimativa do erro de aproximação. Formas indeterminadas e regra de l’Hôspital: enunciado da regra, cuidados necessários à sua aplicação ao cálculo de limites (checar se a expressão no limite é uma forma indeterminada do tipo 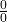 ou
ou 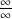 !), aplicação da regra de l’Hôspital ao cálculo de limites para formas indeterminadas do tipo
!), aplicação da regra de l’Hôspital ao cálculo de limites para formas indeterminadas do tipo 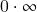 ,
,  e limites do tipo
e limites do tipo 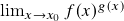 (formas indeterminadas do tipo
(formas indeterminadas do tipo 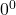 ,
, 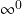 e
e 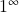 ), aplicações sucessivas da regra de l’Hôspital e cuidados necessários associados.
), aplicações sucessivas da regra de l’Hôspital e cuidados necessários associados. - Aula 12 – 20.3.24 – Limites infinitos e limites no infinito: definição, propriedades e exemplos. Assíntotas: definição geral, interpretação geométrica de limites infinitos ( = assíntotas verticais) e limites no infinito ( = assíntotas horizontais), assíntotas oblíquas. Roteiro para esboço de gráficos de uma função
 contínua com
contínua com  e
e 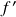 possuindo um número finito de pontos críticos: 1.) Determinação do domínio de
possuindo um número finito de pontos críticos: 1.) Determinação do domínio de 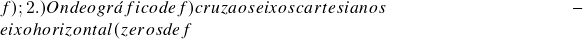 – determinação aproximada usando os passos 3.) e 4.) juntamente com o Teorema do Valor Intermediário) e eixo vertical (valor de
– determinação aproximada usando os passos 3.) e 4.) juntamente com o Teorema do Valor Intermediário) e eixo vertical (valor de  em zero); 3.) Determinação dos pontos críticos de
em zero); 3.) Determinação dos pontos críticos de  no seu domínio e respectivos valores críticos, determinação dos intervalos abertos no domínio de
no seu domínio e respectivos valores críticos, determinação dos intervalos abertos no domínio de  onde
onde 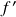 tem sinal definido (diagrama de sinais de
tem sinal definido (diagrama de sinais de 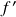 :
: 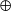 –
– 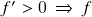 é estritamente crescente no intervalo;
é estritamente crescente no intervalo;  –
– 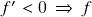 é estritamente decrescente no intervalo); 4.) Determinação dos pontos críticos de
é estritamente decrescente no intervalo); 4.) Determinação dos pontos críticos de 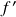 no domínio de
no domínio de  , determinação dos intervalos abertos no domínio de
, determinação dos intervalos abertos no domínio de  onde
onde 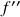 tem sinal definido (diagrama de sinais de
tem sinal definido (diagrama de sinais de 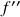 :
: 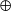 –
– 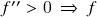 é convexa no intervalo;
é convexa no intervalo;  –
– 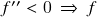 é côncava no intervalo)
é côncava no intervalo)  determinação dos pontos de máximo e mínimo locais de
determinação dos pontos de máximo e mínimo locais de  usando o diagrama de sinais de
usando o diagrama de sinais de 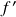 (critério da derivada primeira) ou o diagrama de sinais de
(critério da derivada primeira) ou o diagrama de sinais de 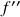 (critério da derivada segunda), determinação dos pontos de inflexão de
(critério da derivada segunda), determinação dos pontos de inflexão de  usando o diagrama de sinais de
usando o diagrama de sinais de 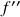 ; 5.) Assíntotas de
; 5.) Assíntotas de  (se existirem).
(se existirem). - Aula 11 – 18.3.24 – Funções convexas ( = “côncavas por cima”) e côncavas ( = “côncavas por baixo”): definição e propriedades – 1.)
 convexa (resp. côncava)
convexa (resp. côncava) 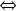
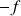 côncava (resp. convexa), 2.)
côncava (resp. convexa), 2.)  convexa ou côncava em
convexa ou côncava em ![Rendered by QuickLaTeX.com [a,b]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-18110494e358fb03cd7f5ed3a6adf7ce_l3.png)

 contínua em
contínua em 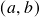 , 3.)
, 3.) 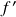 crescente (resp. decrescente)
crescente (resp. decrescente) 
 convexa (resp. côncava) 4.)
convexa (resp. côncava) 4.) 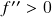 (resp.
(resp. 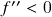 )
) 
 convexa (resp. côncava). Máximos e mínimos de funções (iii): determinação de máximos e mínimos locais (ii) – o critério da segunda derivada. Pontos de inflexão.
convexa (resp. côncava). Máximos e mínimos de funções (iii): determinação de máximos e mínimos locais (ii) – o critério da segunda derivada. Pontos de inflexão. - Aula 10 – 13.3.24 – Máximos e mínimos de funções (ii): recapitulação – nomenclatura (pontos de máximo / mínimo globais (absolutos) / locais (relativos) e (valores) máximos / mínimos globais (absolutos) / locais (relativos), pontos de extremo globais (absolutos) / locais (relativos) e (valores) extremos globais (absolutos) / locais (relativos)), critérios básicos para a determinação de máximos e mínimos (Teorema do Valor Extremo (TVE) e critério de Fermat, pontos críticos e valores críticos). Consequências conjuntas do TVE e do critério de Fermat (ii): teorema de Rolle e aplicações (número de zeros de uma função e de sua derivada), teorema do valor médio (TVM) e TVM generalizado, propriedade do valor intermediário (PVI) para derivadas. Consequências do TVM: como o sinal da derivada determina a monotonicidade da função. Determinação de máximos e mínimos locais (i): o critério da primeira derivada.
- Aula 9 – 11.3.24 – Máximos e mínimos de funções (i): nomenclatura – pontos de máximo / mínimo globais (absolutos) / locais (relativos) e (valores) máximos / mínimos globais (absolutos) / locais (relativos), pontos de extremo globais (absolutos) / locais (relativos) e (valores) extremos globais (absolutos) / locais (relativos). Exemplos e contra-exemplos de existência de máximos e mínimos. Critérios básicos para a determinação de máximos e mínimos: o Teorema do Valor Extremo (TVE) e o critério de Fermat, pontos críticos e valores críticos. Método para a determinação de máximos e mínimos globais de funções contínuas num intervalo fechado e limitado com um número finito de pontos críticos. Consequências conjuntas do TVE e do critério de Fermat (i): o teorema de Rolle e o teorema do valor médio.
- Aula 8 – 6.3.24 – Aplicações da regra da cadeia (ii): problemas de taxas relacionadas – exemplo e forma geral. Derivadas de ordem superior: definição e exemplos, polinômios de Taylor.
- Aula 7 – 4.3.24 – Regras de cálculo de derivadas (vi): recapitulação – propriedades de funções exponenciais e logarítmicas a partir do caso de expoentes racionais. Derivadas de funções exponenciais e logarítmicas (ii): quociente de Newton de uma função exponencial e limite fundamental associado, consequências da existência do limite fundamental – o logaritmo natural e a exponencial natural, fórmulas para as derivadas de funções exponenciais e logarítmicas, expressão da função logarítmica de base
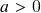 ,
, 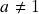 em termos do logaritmo natural, mudança de base de logaritmos. Prova da existência e positividade do limite fundamental
em termos do logaritmo natural, mudança de base de logaritmos. Prova da existência e positividade do limite fundamental 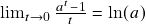 para o quociente de Newton da função exponencial de base
para o quociente de Newton da função exponencial de base 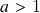 . Aplicações: 1.) “regra do tombo” vale para qualquer expoente real, 2.) uso da fórmula
. Aplicações: 1.) “regra do tombo” vale para qualquer expoente real, 2.) uso da fórmula 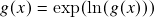 para o cálculo da derivada de funções da forma
para o cálculo da derivada de funções da forma 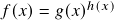 com
com 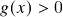 , derivada logarítmica.
, derivada logarítmica. - Aula 6 – 28.2.24 – Regras de cálculo de derivadas (v): recapitulação – funções trigonométricas básicas e suas derivadas a partir de
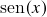 . Funções trigonométricas inversas (ii): definição e cálculo da derivada pela regra da inversa, o papel das relações trigonométricas (continuação). Aplicações da regra da cadeia (i): funções definidas implicitamente, derivação implícita. Derivadas de funções exponenciais e logarítmicas (i): propriedades de funções exponenciais e logarítmicas a partir do caso de expoentes racionais, quociente de Newton de uma função exponencial e limite fundamental associado, o logaritmo natural e a exponencial natural, fórmulas para as derivadas de funções exponenciais e logarítmicas.
. Funções trigonométricas inversas (ii): definição e cálculo da derivada pela regra da inversa, o papel das relações trigonométricas (continuação). Aplicações da regra da cadeia (i): funções definidas implicitamente, derivação implícita. Derivadas de funções exponenciais e logarítmicas (i): propriedades de funções exponenciais e logarítmicas a partir do caso de expoentes racionais, quociente de Newton de uma função exponencial e limite fundamental associado, o logaritmo natural e a exponencial natural, fórmulas para as derivadas de funções exponenciais e logarítmicas. - Aula 5 – 26.2.24 – Regras de cálculo de derivadas (iv): recapitulação – regras de cálculo de derivadas (regras da soma, do múltiplo, do produto = Leibniz, da recíproca e do quociente, regra da cadeia = derivada de funções compostas, regra da inversa = derivada de funções inversas), exemplos de aplicação da regra da inversa e da regra da cadeia (ver exemplos (iii) da Aula 4). Derivadas das funções trigonométricas básicas: derivada de
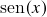 – regras de adição, redução ao limite fundamental
– regras de adição, redução ao limite fundamental 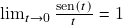 , dedução geométrica do limite fundamental pelo Teorema do Confronto. Expressão das demais funções trigonométricas básicas em termos de
, dedução geométrica do limite fundamental pelo Teorema do Confronto. Expressão das demais funções trigonométricas básicas em termos de 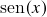 e suas derivadas. Funções trigonométricas inversas (i): definição e cálculo da derivada pela regra da inversa, o papel das relações trigonométricas.
e suas derivadas. Funções trigonométricas inversas (i): definição e cálculo da derivada pela regra da inversa, o papel das relações trigonométricas. - Aula 4 – 21.2.24 – Regras de cálculo de derivadas (iii): recapitulação – regra da cadeia (derivada de funções compostas – enunciado, notação de Leibniz versus notação de Lagrange e prova). Problemas com a “prova” da regra da cadeia sugerida pela notação de Leibniz. Subproduto da prova da regra da cadeia: linearização de uma função ao redor de um ponto onde ela é derivável = “melhor” aproximação linear ao redor desse ponto, erro de linearização. Regra da inversa (derivada de funções inversas): interlúdio – Teorema do Valor Intermediário (TVI), propriedade do valor intermediário (PVI) e Teorema do Valor Extremo (TVE), caracterização de funções contínuas injetoras num intervalo fechado e de suas inversas em termos da PVI. Enunciado e prova da regra da inversa. Exemplos (iii): 6.) “regra do tombo” para raízes
 -ésimas (
-ésimas (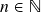 ) e 7.) para potências racionais.
) e 7.) para potências racionais. - Aula 3 – 19.2.23 – Derivadas (ii): recapitulação – definição formal, quocientes de Newton, funções deriváveis num ponto, regras de cálculo de derivadas (i) (somas, múltiplos por reais, produtos, recíprocas e quocientes). Exemplos (ii) – 4.) derivadas de funções racionais, 5.) “regra do tombo” para expoentes inteiros negativos. Regras de cálculo de derivadas (ii) – regra da cadeia (enunciado e prova). Exemplos (iii) – 5.) a regra da recíproca como caso particular. Derivadas de funções trigonométricas – a função seno, relação com limite fundamental, motivação geométrica.
- Aula 2 – 7.2.23 – Derivadas (i): definição formal, quocientes de Newton, funções deriváveis num ponto. Interpretação do quociente de Newton de uma função como taxa de variação média e como inclinação da reta secante ao seu gráfico em dois pontos distintos, interpretação da derivada de uma função como taxa de variação instantânea e como inclinação da reta tangente ao seu gráfico num ponto. Continuidade de uma função nos pontos onde ela é derivável. Regras de cálculo de derivadas (i) – somas, múltiplos por reais, produtos (regra de Leibniz), recíprocas e quocientes (enunciado e prova). Exemplos (i) – 0.) funções constantes, 1.) f(x)=x, 2.) derivada de potências naturais de x (“regra do tombo”), 3.) derivadas de funções polinomiais.
- Aula 1 – 5.2.23 – Informações sobre o funcionamento do curso. Motivação: uma breve perspectiva histórica sobre o cálculo diferencial e integral – cálculo de áreas (método de exaustão – Eudoxo e Arquimedes), máximos e mínimos de funções e sua relação com a inclinação (horizontal) da reta tangente ao gráfico da função nos pontos de máximo e mínimo (Fermat), taxas de variação média e instantânea, a relação do cálculo de tangentes com o cálculo de áreas em Cinemática (Newton).
Bibliografia
Listamos aqui os textos que seguiremos mais de perto.
- Tom M. Apostol, Cálculo, Volume 1 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume I – Second Edition. Wiley, 1967).
- Michael Spivak, Calculus (3a. edição). Publish or Perish, 1994.
- James Stewart, Cálculo, Volume 1 (6a. edição). Cengage Learning, 2012.
Textos suplementares:
- Hamilton L. Guidorizzi, Um Curso de Cálculo, Volume 1 (5a. edição). Editora LTC, 2001.
- Armando Caputi, Cristian F. Coletti e Daniel Miranda – Notas de Aula de Cálculo I (online).
- Walter Rudin, Principles of Mathematical Analysis (3a. edição). McGraw-Hill, 1976.
- Apex Calculus (online, serve como referência para as notas de aula dos profs. Caputi, Coletti e Miranda citadas acima).
Recomendações e material didático suplementar
Faremos uso tácito de conceitos vistos na disciplina BIS0003 – Bases Matemáticas, particularmente das noções de limite e continuidade (capítulo 9 das notas de aula dos profs. Armando Caputi e Daniel Miranda). Recomendamos fortemente que @ participante com dificuldades nesses tópicos faça uma revisão destes, pois isto não será feito em aula.
A UFABC possui um canal no YouTube para a disciplina de FUV, com vídeos de aulas remotas de quadrimestres anteriores. Uma seleção de vídeos para estudo individual também pode ser encontrada no cronograma unificado do Gradmat para a disciplina de FUV.
Para auxiliar a visualização de gráficos de funções no estudo individual, recomendamos os softwares GeoGebra e o aplicativo Web Symbolab. Para mais sugestões de software, recomendamos visitar a página do Gradmat para a disciplina de FUV.
Avaliação
- Média preliminar:
Mp = 0,5*(P1+P2) + 0,15*Mt , onde Mt é a média dos testes online no Moodle (valendo de 0 a 10). - Média final:
Mp = 0,5*max(P1+P2, Rec+P1, Rec+P2) + 0,15*Mt - Critério de conversão de média preliminar (Mp) / final (Mf) para conceito preliminar (Cp) / final (Cf):
Cp (resp. Cf) = F – Mp (resp. Mf) < 4,5;
Cp (resp. Cf) = D – Mp (resp. Mf) = 4,5-5,2;
Cp (resp. Cf) = C – Mp (resp. Mf) = 5,3-6,9;
Cp (resp. Cf) = B – Mp (resp. Mf) = 7,0-8,4;
Cp (resp. Cf) = A – Mp (resp. Mf) = 8,5-10,0. - Haverá uma prova substitutiva e uma prova de recuperação no final do curso. O conteúdo de ambas as provas compreenderá toda a matéria.
- A prova substitutiva só poderá ser feita por participantes que não puderem comparecer a uma das provas, com justificativa formal por escrito da ausência entregue ao docente no máximo até o horário de início da prova substitutiva. Preferencialmente o documento físico original deve ser entregue; se não por possível (e.g. pelo mesmo ser exigido para justificar ausência em provas de outras disciplinas), será aceita uma cópia digitalizada enviada por email mas será exigido nesse caso que @ participante apresente o documento original para conferência dentro do mesmo prazo.
- A prova de recuperação será aplicada no início do 2q’24, em data e local a serem divulgados futuramente. Apenas participantes que ficaram com conceitos preliminares D e F (ver critério acima) após a aplicação da prova substitutiva poderão fazer essa prova.
- Datas das provas:
P1 – 27.3 (quarta-feira);
P2 – 3.5 (sexta-feira);
Sub – 7.5 (terça-feira, se houver necessidade);
Rec – início do segundo quadrimestre de 2024, a divulgar. - Atenção: Como a data da P2 é destinada à reposição do feriado de 14.2 (quarta-feira de Cinzas) e a data da Sub é destinada à reposição da ponte de feriado de 8.4 (segunda-feira, aniversário de Santo André), essas provas seguirão os horários e locais das aulas no dia da semana em que tenha caído o respectivo feriado sendo reposto. Ver calendário de reposição de feriados para mais detalhes.
Listas de exercícios
As listas de exercícios do Gradmat podem ser encontradas aqui:
É extremamente importante que @s participantes façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!
@s participantes que assim desejarem poderão entregar as suas resoluções das listas correspondentes à matéria de cada prova até a aula seguinte a prova correspondente (P1 – 20.3; P2 – data da Sub). Tais listas serão avaliadas nos casos de média final limítrofe para aprovação (ver tabela de conversão de conceitos acima), convertendo-se num bônus de até 1,0 ponto na média final.
Testes online (Moodle)
Haverá quatro (4) testes online na plataforma Moodle. @s participantes deverão receber as informações detalhadas sobre cada teste diretamente nos seus emails institucionais ((at)aluno.ufabc.edu.br), e deverão logar-se na plataforma com seu login e senha institucionais para fazer os testes.
Os exercícios cobertos nos testes online constituem uma seleção mínima de exercícios e não substituem a resolução das listas de exercícios do Gradmat, que são mais abrangentes e completas.
Cronograma de janelas de resolução dos testes:
- Teste 1 – 23.2 a 27.2;
- Teste 2 – 22.3 a 26.3;
- Teste 3 – 5.4 a 9.4;
- Teste 4 – 26.4 a 30.4.
Monitoria e plantão de dúvidas
A partir de segunda-feira, 19.2 haverá monitoria presencial nas seguintes datas e horários:
- José Roberto Galdino Serra – 2as. feiras, 14h00-15h30, sala A-S311-1 (campus SA);
- Marcel Morimoto – 5as. feiras, 16h00-18h00, sala A-S311-1 (campus SA);
- Pedro Emanuel Verolese Lopes – 6as. feiras, 12h00-13h30, sala A-S309-3 (campus SA).
Haverá também atendimento online síncrono por videoconferência (Google Meet, Discord e Telegram) a partir de terça-feira, 20.2 nos seguintes horários:
- José Roberto Galdino Serra – 3as. feiras, 17h00-18h00 e 6as. feiras, 10h00-12h00 – sala Google Meet;
- Marcel Morimoto – 4as. feiras, 17h00-18h00 e sábados, 14h00-16h00 – sala Discord;
- Pedro Emanuel Verolese Lopes – 6as. feiras, 16h00-17h00 e sábados, 12h00-14h00 – Telegram.
Haverá também um plantão de dúvidas por videoconferência (Google Meet) às terças-feiras das 18h00 às 20h00, que terá início em 6.2. Para acessar a sala de reunião será necessário usar a conta Google vinculada ao endereço de email institucional da UFABC ((at)aluno.ufabc.edu.br). Veja o tutorial do NTI https://www.youtube.com/watch?v=Rf4kIbb4_sk para fazer a vinculação caso isso já não tenha sido feito. Reitero que o acesso à sala será tacitamente negado a contas Google que não satisfaçam a essa condição, por razões de segurança. O link da sala será divulgado por email pouco (no máximo 30 minutos) antes do início de cada plantão.
Finalmente, o Moodle terá um fórum aberto de perguntas e respostas onde @s participantes poderão tirar suas dúvidas assincronamente com o docente e/ou colegas.
Roteiro
Seguiremos de maneira aproximada o cronograma unificado do Gradmat para a disciplina de FUV, com algumas modificações a serem indicadas quando necessário.
- Derivadas: Definição, interpretação geométrica, regras de derivação (soma, produto, quociente, regra da cadeia e função inversa), derivadas de funções elementares (polinomial, potência, trigonométrica, logarítmica, exponencial), derivadas de ordem superior. Aplicações de derivadas: máximos e mínimos, crescimento e decrescimento, concavidade, interpretação de gráficos, teorema do valor médio de Cauchy, regra de L’Hospital, otimização. Fórmula de Taylor.
- Integrais: área sob uma curva e as somas de Riemann, integral definida, propriedades da integral definida, teorema fundamental do cálculo, cálculo de áreas entre curvas, integral indefinida. Métodos de integração: integração por mudança de variável, integração por partes, integração de funções racionais por frações parciais, integração de potências de funções trigonométricas. Aplicações do cálculo integral: comprimentos de arcos, áreas e volumes de sólidos por revolução.

