
Esta é a página sobre a disciplina BCN0407 – Funções de Várias Variáveis, ministrada no primeiro quadrimestre de 2025 para as seguintes turmas:
- A2 – Noturno, campus Santo André – horário: 3as. feiras 19h00-21h00 e 5as. feiras 21h00-23h00, sala A-S103-0-SA.
- B2 – Noturno, campus Santo André – horário: 3as. feiras 21h00-23h00 e 5as. feiras 19h00-21h00, sala A-S101-0-SA.
Aqui encontram-se informações específicas sobre as turmas acima – informações gerais sobre o curso podem ser encontradas na página do Gradmat para a disciplina de FVV.
Aulas
Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.
- (6.5.25) Integrais múltiplas (iv): recapitulação – regiões mensuráveis (definição em termos de funções características, caracterização em termos do conteúdo
 -dimensional nulo da fronteira), integral numa região mensurável, subdivisão de uma região mensurável em partes e aditividade da integral, integrais iteradas e regiões de tipo
-dimensional nulo da fronteira), integral numa região mensurável, subdivisão de uma região mensurável em partes e aditividade da integral, integrais iteradas e regiões de tipo 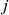 em
em  . Exemplos de integrais duplas em regiões de tipos 1 e 2. Aplicações de integrais múltiplas: 1.) volumes
. Exemplos de integrais duplas em regiões de tipos 1 e 2. Aplicações de integrais múltiplas: 1.) volumes  -dimensionais, áreas (
-dimensionais, áreas (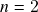 ) e volumes (
) e volumes (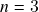 ); 2.) massa (resp. carga) total numa região mensurável com densidade de massa (resp. carga) contínua; 3.) distribuições de probabilidade contínuas e valores esperados ( = valores médios = médias (ponderadas)) de funções contínuas numa região mensurável com respeito a uma distribuição contínua de probabilidade. Casos particulares de 3.) – centro de massa e centroide ( = baricentro) de uma região mensurável, tensor de inércia. Mudança de variáveis em integrais múltiplas: enunciado, o papel do determinante jacobiano da mudança de variáveis, exemplos – coordenadas polares, cilíndricas e esféricas (Apostol: Seções 11.12 a 11.14, 11.16 e 11.26, Stewart: Seções 15.3 a 15.9).
); 2.) massa (resp. carga) total numa região mensurável com densidade de massa (resp. carga) contínua; 3.) distribuições de probabilidade contínuas e valores esperados ( = valores médios = médias (ponderadas)) de funções contínuas numa região mensurável com respeito a uma distribuição contínua de probabilidade. Casos particulares de 3.) – centro de massa e centroide ( = baricentro) de uma região mensurável, tensor de inércia. Mudança de variáveis em integrais múltiplas: enunciado, o papel do determinante jacobiano da mudança de variáveis, exemplos – coordenadas polares, cilíndricas e esféricas (Apostol: Seções 11.12 a 11.14, 11.16 e 11.26, Stewart: Seções 15.3 a 15.9). - (29.4.25) Integrais múltiplas (iii): recapitulação – propriedades da integral (linearidade = somas e múltiplos de funções integráveis são integráveis, e somas e múltiplos podem ser postos “para fora” da integral, composição de funções contínuas de uma variável com funções integráveis são integráveis
![Rendered by QuickLaTeX.com \Rightarrow f^2, |f|, fg=\frac{1}{2}[(f+g)^2-f^2-g^2]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-8c03fb2129a6931abba34189e25e2abd_l3.png) são integráveis se
são integráveis se 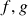 também são, positividade =
também são, positividade = 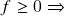 a integral de
a integral de  é não-negativa), caracterização das funções integráveis (o subconjunto dos pontos de descontinuidade tem conteúdo
é não-negativa), caracterização das funções integráveis (o subconjunto dos pontos de descontinuidade tem conteúdo  -dimensional nulo), funções que se anulam fora de um subconjunto de conteúdo
-dimensional nulo), funções que se anulam fora de um subconjunto de conteúdo  -dimensional nulo tem integral zero, regiões mensuráveis (definição em termos de funções características, caracterização em termos do conteúdo
-dimensional nulo tem integral zero, regiões mensuráveis (definição em termos de funções características, caracterização em termos do conteúdo  -dimensional nulo da fronteira), integral numa região mensurável, subdivisão de uma região mensurável em partes e aditividade da integral. Integrais iteradas e Teorema de Fubini: enunciado e exemplos, regiões de tipo
-dimensional nulo da fronteira), integral numa região mensurável, subdivisão de uma região mensurável em partes e aditividade da integral. Integrais iteradas e Teorema de Fubini: enunciado e exemplos, regiões de tipo 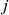 em
em  (Stewart: Seções 15.1 e 15.3, Apostol: Seções 11.1 a 11.8 e 11.10 e 11.12).
(Stewart: Seções 15.1 e 15.3, Apostol: Seções 11.1 a 11.8 e 11.10 e 11.12). - (24.4.25) Integrais múltiplas (ii): recapitulação – retângulos
 -dimensionais (fechados) e construção da integral (de Riemann)
-dimensionais (fechados) e construção da integral (de Riemann)  -dimensional, funções (Riemann-)integráveis num retângulo
-dimensional, funções (Riemann-)integráveis num retângulo  -dimensional. Propriedades da integral: linearidade (somas e múltiplos de funções integráveis são integráveis, e somas e múltiplos podem ser postos “para fora” da integral), composição de funções contínuas de uma variável com funções integráveis são integráveis (
-dimensional. Propriedades da integral: linearidade (somas e múltiplos de funções integráveis são integráveis, e somas e múltiplos podem ser postos “para fora” da integral), composição de funções contínuas de uma variável com funções integráveis são integráveis ( ![Rendered by QuickLaTeX.com \Rightarrow f^2, |f|, fg=\frac{1}{2}[(f+g)^2-f^2-g^2]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-8c03fb2129a6931abba34189e25e2abd_l3.png) são integráveis se
são integráveis se 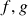 também são), positividade (
também são), positividade (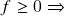 a integral de
a integral de  é não-negativa). Integral de funções constantes, subconjuntos de conteúdo
é não-negativa). Integral de funções constantes, subconjuntos de conteúdo  -dimensional nulo ( = medida
-dimensional nulo ( = medida  -dimensional nula), caracterização das funções integráveis (o subconjunto dos pontos de descontinuidade tem conteúdo
-dimensional nula), caracterização das funções integráveis (o subconjunto dos pontos de descontinuidade tem conteúdo  -dimensional nulo), funções que se anulam fora de um subconjunto de conteúdo
-dimensional nulo), funções que se anulam fora de um subconjunto de conteúdo  -dimensional nulo tem integral zero. Regiões mensuráveis: definição em termos de funções características, caracterização em termos do conteúdo
-dimensional nulo tem integral zero. Regiões mensuráveis: definição em termos de funções características, caracterização em termos do conteúdo  -dimensional nulo da fronteira, integral numa região mensurável. Subdivisão de uma região mensurável em partes e aditividade da integral (Stewart: Seções 15.1 e 15.3, Apostol: Seções 11.1 a 11.5, 11.7, 11.11 e 11.12).
-dimensional nulo da fronteira, integral numa região mensurável. Subdivisão de uma região mensurável em partes e aditividade da integral (Stewart: Seções 15.1 e 15.3, Apostol: Seções 11.1 a 11.5, 11.7, 11.11 e 11.12). - (22.4.25) Integrais múltiplas (i): preliminares – retângulos
 -dimensionais (fechados) e funções limitadas. Recapitulação: construção da integral de Riemann de funções de uma variável – partições de um intervalo fechado, somas de Riemann superior e inferior com respeito a uma partição, soma de Riemann com respeito a uma partição e uma marcação da última, integrais de Riemann superior e inferior, funções (Riemann-)integráveis e integral (de Riemann) de uma função num intervalo. Integrais múltiplas num retângulo
-dimensionais (fechados) e funções limitadas. Recapitulação: construção da integral de Riemann de funções de uma variável – partições de um intervalo fechado, somas de Riemann superior e inferior com respeito a uma partição, soma de Riemann com respeito a uma partição e uma marcação da última, integrais de Riemann superior e inferior, funções (Riemann-)integráveis e integral (de Riemann) de uma função num intervalo. Integrais múltiplas num retângulo  -dimensional: partições
-dimensional: partições  -dimensionais e somas de Riemann (superior/inferior) com respeito a uma partição, soma de Riemann com respeito a uma partição
-dimensionais e somas de Riemann (superior/inferior) com respeito a uma partição, soma de Riemann com respeito a uma partição  -dimensional e uma marcação da última, integrais de Riemann inferior e superior num retângulo
-dimensional e uma marcação da última, integrais de Riemann inferior e superior num retângulo  -dimensional, funções (Riemann-)integráveis e integral (de Riemann) num retângulo
-dimensional, funções (Riemann-)integráveis e integral (de Riemann) num retângulo  -dimensional (Stewart: Seção 15.1, Apostol: Seções 11.1 a 11.5).
-dimensional (Stewart: Seção 15.1, Apostol: Seções 11.1 a 11.5). - (17.4.25) Máximos e mínimos de funções de várias variáveis (iii): recapitulação – critério da derivada segunda para classificação de pontos críticos, caso particular de duas variáveis. Exemplos de cada instância do critério da segunda derivada em duas variáveis. Máximos e mínimos sujeitos a vínculos ( = restrições), multiplicadores de Lagrange (Stewart: Seções 14.7 e 14.8, Apostol: Seções 9.11, 9.12 e 9.14).
- (15.4.25) Máximos e mínimos de funções de várias variáveis (ii): interlúdio – fórmula de Taylor de segunda ordem (com resto) para funções de várias variáveis, matriz hessiana. Critério da derivada segunda para determinar quando um ponto crítico é ponto de mínimo / máximo local (matriz hessiana positiva definida / negativa definida no ponto crítico) ou um ponto de sela (matriz hessiana indefinida no ponto crítico), caso de inconclusividade do critério da derivada segunda. Forma do critério da derivada segunda para duas variáveis em termos do determinante da matriz hessiana no ponto crítico (Stewart: Seção 14.7, Apostol: Seções 9.9 a 9.12).
- (10.4.25) Máximos e mínimos de funções de várias variáveis (i): definições e nomenclatura – pontos de mínimo, de máximo e de extremo ( = globais ou absolutos), (valores) mínimos, máximos e extremos ( = globais ou absolutos) de uma função, pontos de mínimo, de máximo e de extremo locais ( = relativos), (valores) mínimos, máximos e extremos locais ( = relativos) de uma função. Teorema do Valor Extremo (funções contínuas em domínios fechados e limitados de
 tem mínimo e máximo). Critério de Fermat para candidatos a pontos de extremo locais, pontos críticos ( = estacionários) e valores críticos ( = estacionários), interpretação geométrica (hiperplano tangente ao gráfico num ponto crítico é horizontal). Exemplos de pontos críticos, pontos de sela (Stewart: Seção 14.7, Apostol: Seção 9.9).
tem mínimo e máximo). Critério de Fermat para candidatos a pontos de extremo locais, pontos críticos ( = estacionários) e valores críticos ( = estacionários), interpretação geométrica (hiperplano tangente ao gráfico num ponto crítico é horizontal). Exemplos de pontos críticos, pontos de sela (Stewart: Seção 14.7, Apostol: Seção 9.9). - (3.4.25) Derivadas parciais de ordem superior: derivadas parciais de segunda ordem – definição e notação. O problema da igualdade das derivadas parciais mistas de segunda ordem com respeito à mudança da ordem das variáveis das derivadas parciais: um contra-exemplo. Critério para igualdade das derivadas parciais mistas de segunda ordem: teoremas de Clairaut e de Schwarz, funções (de classe)
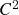 . Derivadas parciais de ordem
. Derivadas parciais de ordem 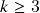 : definição por indução em
: definição por indução em 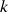 e notação, funções (de classe)
e notação, funções (de classe) 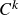 . Equações diferenciais parciais: soluções e exemplos (Stewart: Seção 14.3, Apostol: Seções 8.8, 8.23 e 9.1 a 9.5).
. Equações diferenciais parciais: soluções e exemplos (Stewart: Seção 14.3, Apostol: Seções 8.8, 8.23 e 9.1 a 9.5). - (27.3.25) Diferenciabilidade (iii): recapitulação – funções e aplicações diferenciáveis, critério de diferenciabilidade, funções continuamente diferenciáveis. Regra da Cadeia para a diferencial de aplicações compostas (ii): enunciado e forma matricial (multiplicação de matrizes jacobianas), exemplos de casos particulares – 1.) derivada total ao longo de uma curva, 2.) composta de uma função com uma aplicação. Interpretação do vetor gradiente como normal a (vetores tangentes a) conjuntos de nível, equação do (hiper)plano tangente a um conjunto de nível num ponto. Derivadas direcionais como taxas de variação, direções com taxa de variação máxima e mínima (deisgualdade de Cauchy-Schwarz). Derivação implícita: equações de função implícita e suas soluções ( = funções definidas implicitamente), cálculo de derivadas parciais implícitas a partir da equação de função implícita usando a Regra da Cadeia (Stewart: Seções 14.4 a 14.6, Apostol: Seções 8.18, 8.20, 8.21 e 9.6).
- (25.3.25) Diferenciabilidade (ii): recapitulação – funções e aplicações diferenciáveis (definição e consequências – 1.) identificação da diferencial da função com o vetor gradiente, 2.) existência de derivadas direcionais, 3.) continuidade), diferencial e matriz jacobiana de uma aplicação diferenciável. Regra da Cadeia para a diferencial de aplicações compostas (i): enunciado e forma matricial (multiplicação de matrizes jacobianas). Casos particulares da Regra da Cadeia: derivadas parciais da composição de uma função com uma aplicação, derivada total ao longo de uma curva parametrizada. Critério de diferenciabilidade: enunciado e consequências, funções continuamente diferenciáveis (Stewart: Seções 14.4 a 14.6, Apostol: Seções 8.11 a 8.13 e 8.15).
- (20.3.25) Diferenciabilidade (i): recapitulação – derivadas parciais e derivadas direcionais, aproximação linear para funções deriváveis de uma variável (lema de Hadamard), retas tangentes ao gráfico de uma função de várias variáveis ao longo de cada variável e o hiperplano gerado por essas retas, vetor gradiente, protótipo de aproximação linear para funções de várias variáveis, problemas com o erro da aproximação linear para funções de várias variáveis. Funções diferenciáveis: definição e consequências – 1.) identificação da diferencial da função com o vetor gradiente, 2.) existência de derivadas direcionais, 3.) continuidade. Aplicações diferenciáveis, diferencial e matriz jacobiana de uma aplicação diferenciável (Stewart: Seções 14.3 e 14.4, Apostol: Seções 8.6, 8.7, 8.11 e 8.12).
- (18.3.25) Derivadas parciais (ii): recapitulação – derivadas parciais e derivadas direcionais. Erro da aproximação linear gerada pela derivada direcional. Retas tangentes ao gráfico de uma função de várias variáveis ao longo de cada variável e o hiperplano gerado por essas retas. O (vetor) gradiente de uma função num ponto, protótipo de aproximação linear para funções de várias variáveis. Problemas com o erro da aproximação linear para funções de várias variáveis – um contra-exemplo (Stewart: Seção 14.3, Apostol: Seções 8.6, 8.7 e 8.10).
- (13.3.25) Derivadas parciais (i): definição – o caso particular de funções de duas variáveis, interpretação geométrica, definição geral para funções de
 variáveis. Derivadas direcionais: definição, regras de cálculo e propriedades. Por que a existência de derivadas direcionais não garante para funções de várias variáveis as consequências da diferenciabilidade de funções de uma variável (continuidade, aproximação linear) – um contra-exemplo. Necessidade de revisitar o conceito de diferenciabilidade para funções de várias variáveis com base na ideia de aproximação linear (Stewart: Seção 14.3, Apostol: Seções 8.6, 8.7 e 8.10).
variáveis. Derivadas direcionais: definição, regras de cálculo e propriedades. Por que a existência de derivadas direcionais não garante para funções de várias variáveis as consequências da diferenciabilidade de funções de uma variável (continuidade, aproximação linear) – um contra-exemplo. Necessidade de revisitar o conceito de diferenciabilidade para funções de várias variáveis com base na ideia de aproximação linear (Stewart: Seção 14.3, Apostol: Seções 8.6, 8.7 e 8.10). - (11.3.25) Limites e continuidade (iii): recapitulação – limites de funções e aplicações num ponto do fecho do domínio, continuidade de funções e aplicações num ponto do domínio, regras de cálculo de limites (somas, produtos e quocientes de funções, composição de aplicações, composição de funções e aplicações com curvas parametrizadas). Identificando não-existência de limites por meio de limites diferentes para a composição com diferentes curvas parametrizadas – exemplos. Regras de cálculo de limites (ii):o Teorema do Confronto – enunciado e aplicação ao cálculo de limites de produtos de funções quando o limite de um dos fatores pode não existir (Stewart: Seção 14.2, Apostol: Seção 8.4).
- (6.3.25) Limites e continuidade (ii): limites de funções e aplicações num ponto do fecho do domínio, continuidade de funções e aplicações num ponto do domínio – definição e interpretação. Redução do problema de cálculo de limites de aplicações ao cálculo de limites das suas componentes. Regras de cálculo de limites (i): somas, produtos e quocientes de funções, composição de aplicações. Composição de funções e aplicações com curvas parametrizadas. Exemplos (i): funções constantes, componentes em
 , norma euclideana. Regras de cálculo de limites (ii): operações vetoriais. Exemplos (ii): explorando as regras de cálculo de limites juntamente cominformaçẽos sobre limites de funções de uma variável (Stewart: Seção 14.2, Apostol: Seção 8.4).
, norma euclideana. Regras de cálculo de limites (ii): operações vetoriais. Exemplos (ii): explorando as regras de cálculo de limites juntamente cominformaçẽos sobre limites de funções de uma variável (Stewart: Seção 14.2, Apostol: Seção 8.4). - (27.2.25) Domínios em
 (iv): recapitulação – pontos interiores, exteriores e de fronteira de um subconjunto, interior, exterior, fronteira e fecho de um conjunto, subconjuntos abertos e fechados. Exemplos de abertos e fechados de
(iv): recapitulação – pontos interiores, exteriores e de fronteira de um subconjunto, interior, exterior, fronteira e fecho de um conjunto, subconjuntos abertos e fechados. Exemplos de abertos e fechados de  (iv): hiperplanos
(iv): hiperplanos 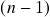 -dimensionais, semiespaços abertos e fechados – o papel do teorema de Pitágoras (minimização da distância de um ponto a um hiperplano) e da desigualdade de Cauchy-Schwarz, analogia com o caso de bolas abertas. Limites e continuidade (i): definição e interpretação (Stewart: Seção 14.2, Apostol: Seções 8.2 e 8.4).
-dimensionais, semiespaços abertos e fechados – o papel do teorema de Pitágoras (minimização da distância de um ponto a um hiperplano) e da desigualdade de Cauchy-Schwarz, analogia com o caso de bolas abertas. Limites e continuidade (i): definição e interpretação (Stewart: Seção 14.2, Apostol: Seções 8.2 e 8.4). - (25.2.25) Domínios em
 (iii): recapitulação – pontos interiores, exteriores e de fronteira de um subconjunto, interior, exterior, fronteira e fecho de um conjunto, subconjuntos abertos e fechados. Uniões e intersecções de abertos (resp. fechados) são abertos (resp. fechados). Exemplos de abertos e fechados de
(iii): recapitulação – pontos interiores, exteriores e de fronteira de um subconjunto, interior, exterior, fronteira e fecho de um conjunto, subconjuntos abertos e fechados. Uniões e intersecções de abertos (resp. fechados) são abertos (resp. fechados). Exemplos de abertos e fechados de  (ii): recapitulação – bolas abertas (caracterização do interior, exterior e da fronteira). O interior (resp. fecho) de um subconjunto é o maior (resp. menor) subconjunto de
(ii): recapitulação – bolas abertas (caracterização do interior, exterior e da fronteira). O interior (resp. fecho) de um subconjunto é o maior (resp. menor) subconjunto de  que está contido em (resp. contém) esse subconjunto. Exemplos de abertos e fechados de
que está contido em (resp. contém) esse subconjunto. Exemplos de abertos e fechados de  (iii): hiperplanos
(iii): hiperplanos 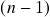 -dimensionais, semiespaços abertos e fechados, retângulos ( = paralelepípedos) abertos e fechados (Apostol: Seção 8.2).
-dimensionais, semiespaços abertos e fechados, retângulos ( = paralelepípedos) abertos e fechados (Apostol: Seção 8.2). - (20.2.25) Domínios em
 (ii): recapitulação – bolas abertas e bolas fechadas
(ii): recapitulação – bolas abertas e bolas fechadas  -dimensionais, esferas (
-dimensionais, esferas (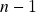 )-dimensionais. Subconjuntos abertos e fechados, pontos interiores, exteriores e de fronteira de um subconjunto. Interior, exterior, fronteira e fecho de um conjunto: definição, relação com o complemento, caracterização de abertos e fechados em termos da fronteira. Exemplos de abertos e fechados de
)-dimensionais. Subconjuntos abertos e fechados, pontos interiores, exteriores e de fronteira de um subconjunto. Interior, exterior, fronteira e fecho de um conjunto: definição, relação com o complemento, caracterização de abertos e fechados em termos da fronteira. Exemplos de abertos e fechados de  (i): bolas abertas – caracterização do interior, exterior e da fronteira (Apostol: Seção 8.2).
(i): bolas abertas – caracterização do interior, exterior e da fronteira (Apostol: Seção 8.2). - (18.2.25) Recapitulação: Interlúdio – geometria euclideana de
 (operações vetoriais e produto escalar, desigualdade de Cauchy-Schwarz e suas consequências, ângulo entre dois vetores não-nulos (“lei dos cossenos”), norma e distância euclideanas, desigualdade triangular). Casos de colinearidade e ortogonalidade para o ângulo entre dois vetores não-nulos, teorema de Pitágoras. Domínios em
(operações vetoriais e produto escalar, desigualdade de Cauchy-Schwarz e suas consequências, ângulo entre dois vetores não-nulos (“lei dos cossenos”), norma e distância euclideanas, desigualdade triangular). Casos de colinearidade e ortogonalidade para o ângulo entre dois vetores não-nulos, teorema de Pitágoras. Domínios em  (i): bolas abertas e bolas fechadas
(i): bolas abertas e bolas fechadas  -dimensionais, esferas (
-dimensionais, esferas (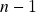 )-dimensionais, subconjuntos abertos e fechados (Stewart: Seção 14.1. Apostol: Seções 8.1 e 8.2).
)-dimensionais, subconjuntos abertos e fechados (Stewart: Seção 14.1. Apostol: Seções 8.1 e 8.2). - (13.2.25) Recapitulação: aplicações ( = campos vetoriais)
 -dimensionais e funções ( = campos escalares) num subconjunto
-dimensionais e funções ( = campos escalares) num subconjunto 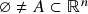 . Gráfico e conjuntos de nível de uma aplicação, exemplos (função altitude num mapa), curvas (resp. superfícies) de nível de uma função de duas (resp. três) variáveis. Problemas com a terminologia de curvas e superfícies de nível: funções constantes, domínios = curvas. Interlúdio: geometria euclideana de
. Gráfico e conjuntos de nível de uma aplicação, exemplos (função altitude num mapa), curvas (resp. superfícies) de nível de uma função de duas (resp. três) variáveis. Problemas com a terminologia de curvas e superfícies de nível: funções constantes, domínios = curvas. Interlúdio: geometria euclideana de  – operações vetoriais e produto escalar. Desigualdade de Cauchy-Schwarz: enunciado e prova. Consequências da desigualdade de Cauchy-Schwarz: ângulo entre dois vetores não-nulos (“lei dos cossenos”), norma e distância euclideanas, desigualdade triangular (Stewart: Seções 12.1 a 12.3 e 14.1. Apostol: Seção 8.1).
– operações vetoriais e produto escalar. Desigualdade de Cauchy-Schwarz: enunciado e prova. Consequências da desigualdade de Cauchy-Schwarz: ângulo entre dois vetores não-nulos (“lei dos cossenos”), norma e distância euclideanas, desigualdade triangular (Stewart: Seções 12.1 a 12.3 e 14.1. Apostol: Seção 8.1). - (11.2.25) Informações sobre o funcionamento do curso. Aplicações de um subconjunto
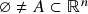 em
em 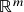 ( = aplicações
( = aplicações  -dimensionais em
-dimensionais em 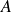 = campos vetoriais
= campos vetoriais  -dimensionais em
-dimensionais em 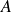 ), funções (de
), funções (de  variáveis) em
variáveis) em 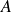 ( = campos escalares em
( = campos escalares em 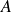 ,
, 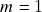 ), componentes de uma aplicação
), componentes de uma aplicação  -dimensional. Curvas parametrizadas
-dimensional. Curvas parametrizadas  -dimensionais (
-dimensionais (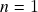 ,
, 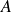 intervalo), imagem de uma curva parametrizada
intervalo), imagem de uma curva parametrizada  -dimensional ( = curva
-dimensional ( = curva  -dimensional). Exemplos de curvas bidimensionais: 1.) gráficos de funções de uma variável – parametrização direta e inversa; 2.) elipses – parametrização por funções trigonométricas (coordenadas polares); 3.) parábolas – parametrização (direta ou inversa) como gráfico de um polinômio de segundo grau; 4.) ramos de hipérboles – parametrização (direta ou inversa) como gráfico, parametrização por funções trigonométricas hiperbólicas (Stewart – Seções 10.1 e 14.1).
-dimensional). Exemplos de curvas bidimensionais: 1.) gráficos de funções de uma variável – parametrização direta e inversa; 2.) elipses – parametrização por funções trigonométricas (coordenadas polares); 3.) parábolas – parametrização (direta ou inversa) como gráfico de um polinômio de segundo grau; 4.) ramos de hipérboles – parametrização (direta ou inversa) como gráfico, parametrização por funções trigonométricas hiperbólicas (Stewart – Seções 10.1 e 14.1).
Bibliografia
Listamos aqui os textos que seguiremos mais de perto.
- Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969);
- Hamilton L. Guidorizzi, Um Curso de Cálculo, Volumes 2 e 3 (5a. edição). Editora LTC, 2001;
- James Stewart, Cálculo, Volume 2 (6a. edição). Cengage Learning, 2012.
Textos suplementares:
- Howard Anton, Irl Bivens, Stephen Davis, Cálculo, Volume II (8a. edição). Bookman, 2007;
- J. E. Marsden, A. J. Tromba, Vector Calculus (5a. edição). W. H. Freeman & Co., 2003;
- Cláudio M. Mendes (ICMC-USP), Notas de Aula (pdf online) – Funções de Várias Variáveis (2005): Diferenciação, Integração.
Recomendações e material didático suplementar
Faremos uso tácito dos conceitos vistos nas disciplinas BCN0402 – Funções de uma Variável e BCN0404 – Geometria Analítica.
Para auxiliar a visualização de gráficos de funções no estudo individual, recomendamos o software GeoGebra. Outro aplicativo excelente com tal finalidade é o CalcPlot3D – uma ferramenta em Java e Javascript de visualização de gráficos de funções de duas variáveis. Ela permite a visualização de vários conceitos de cálculo diferencial em várias variáveis (curvas de nível, funções implícitas, derivadas parciais, plano tangente, gradiente, campos vetoriais, etc.).
Uma seleção de vídeos para estudo individual pode ser encontrada na página do cronograma unificado do curso de FVV.
Avaliação
- Média preliminar:
Mp = 0,3*(P1+P2) + 0,4*Mt, onde Mt é a média dos testes online no Moodle (valendo de 0 a 10). - Média final:
Mp = 0,5*max(P1+P2, Rec+P1, Rec+P2) + 0,15*Mt - Critério de conversão de média preliminar (Mp) / final (Mf) para conceito preliminar (Cp) / final (Cf): Cp (resp. Cf) = F – Mp (resp. Mf) < 4,5;
Cp (resp. Cf) = D – Mp (resp. Mf) = 4,5-5,2;
Cp (resp. Cf) = C – Mp (resp. Mf) = 5,3-6,9;
Cp (resp. Cf) = B – Mp (resp. Mf) = 7,0-8,4;
Cp (resp. Cf) = A – Mp (resp. Mf) = 8,5-10,0. - Haverá uma prova substitutiva e uma prova de recuperação no final do curso. O conteúdo de ambas as provas compreenderá toda a matéria.
- A prova substitutiva só poderá ser feita por participantes que não puderem comparecer a uma das provas, com justificativa formal por escrito da ausência entregue ao docente no máximo até o horário de início da prova substitutiva. Preferencialmente o documento físico original deve ser entregue; se não por possível (e.g. pelo mesmo ser exigido para justificar ausência em provas de outras disciplinas), será aceita uma cópia digitalizada enviada por email mas será exigido nesse caso que @ participante apresente o documento original para conferência dentro do mesmo prazo.
- A prova de recuperação será aplicada no início do 2q’25, em data e local a serem divulgados futuramente. Apenas participantes que ficaram com conceitos preliminares D e F (ver critério acima) após a aplicação da prova substitutiva poderão fazer essa prova.
- Datas das provas:
P1 – 1.4 (terça-feira);
P2 – 13.5 (terça-feira);
Sub – 15.5 (quinta-feira, se houver necessidade);
Rec – início do segundo quadrimestre de 2025, a divulgar.
Listas de exercícios
- Lista 0 ( = Lista 9 GA – revisão de círculos, esferas e cônicas);
- Lista 1;
- Lista 2;
- Lista 3;
- Lista 4;
- Lista 5;
- Lista 6;
- Lista 7.
É extremamente importante que @s participantes façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!
@s participantes que assim desejarem poderão entregar as suas resoluções das listas correspondentes à matéria de cada prova nas seguintes datas:
- P1 – 3.4;
- P2 – data da Rec.
Tais listas serão avaliadas nos casos de média final limítrofe para aprovação (ver tabela de conversão de conceitos acima), convertendo-se num bônus de até 1,5 ponto na média final.
Testes online (Moodle)
Haverá quatro (4) testes online na plataforma Moodle. @s participantes deverão receber as informações detalhadas sobre cada teste diretamente nos seus emails institucionais ((at)aluno.ufabc.edu.br), e deverão logar-se na plataforma com seu login e senha institucionais para fazer os testes.
Os exercícios cobertos nos testes online constituem uma seleção mínima de exercícios e não substituem a resolução das listas de exercícios do Gradmat, que são mais abrangentes e completas.
Cronograma de janelas de resolução dos testes:
- Teste 1 – 13.3 a 17.3;
- Teste 2 – 27.3 a 31.3;
- Teste 3 – 17.4 a 21.4;
- Teste 4 – 8.5 a 12.5.
Monitoria e plantão de dúvidas
A partir de segunda-feira, 17.2 haverá monitoria presencial nas seguintes datas e horários:
- Letícia Caroline Gonçalves – 2as. feiras, 13h00-15h00, sala A-S103-0 (campus SA);
- Gabriel Carmo dos Santos – 2as. feiras, 17h00-19h00 e 4as. feiras, 18h00-19h00, sala A-S103-0 (campus SA);
- Artur Sobral Paulo – 4as. feiras, 13h00-16h00, sala A-S103-0 (campus SA);
- Julia Miki Misumi – 6as. feiras, 13h00-15h00, sala A-S105-0 (campus SA).
Haverá também atendimento online síncrono por videoconferência (Google Meet) aos sábados a partir de 22.2, nos seguintes horários:
- Letícia Caroline Gonçalves – 10h00-11h00;
- Julia Miki Misumi – 14h00-15h00.
Os monitores farão também atendimento online assíncrono no Grupo do Telegram da Monitoria de FVV. Por razões de segurança, os links para as salas de atendimento e do grupo no Telegram não serão disponibilizados aqui e devem ser acessados a partir do plano de ensino no Moodle.
Haverá um plantão de dúvidas às sextas-feiras das 17h00 às 19h00, na minha sala (A-S543-2, Torre 2, Bloco A, campus Santo André). O plantão terá início no dia 14.2.
Finalmente, o Moodle terá um fórum aberto de perguntas e respostas onde @s participantes poderão tirar suas dúvidas assincronamente com o docente e/ou colegas.
Roteiro
Seguiremos de maneira aproximada o cronograma unificado do curso de FVV, com algumas modificações a serem indicadas quando necessário.
- Curvas e parametrização de curvas.
- Funções de várias variáveis: domínios, conjuntos de nível (curvas, superfícies) e esboço de gráficos.
- Limites e continuidade de funções de várias variáveis.
- Derivadas parciais, diferenciabilidade e derivada direcional. Regra da cadeia.
- Funções implícitas.
- Máximos e mínimos, multiplicadores de Lagrange.
- Integrais duplas e triplas, mudança de variáveis.
- Integração em coordenadas polares, cilíndricas e esféricas.
- Aplicações no cálculo de áreas e volumes.

