Plano de ensino – Análise Real I – 1q’25

Esta é a página sobre a disciplina MCBM002 – Análise Real I, ministrada no primeiro quadrimestre de 2025 para a seguinte turma:

A1 – Noturno, campus Santo André – horário: 4as. feiras 19h00-21h00 e 6as. feiras 21h00-23h00, sala A-S301-2-SA.

Aqui encontram-se informações específicas sobre a turma acima.

Aulas

Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.

(25.4.25) Funções em espaços métricos (ii): recapitulação – limites e continuidade de funções em espaços métricos, continuidade da composta. Funções contínuas em (todos os pontos de) um espaço métrico: caracterização global (imagens inversas de abertos são abertas, imagens inversas de fechados são fechadas), imagens de subconjuntos compactos (resp. conexos) por funções contínuas são compactos (resp. conexos) – prova. Caso particular quando a imagem é $\mathbb{R}$ : Teorema do Valor Extremo (resp. Teorema do Valor Intermediário) (Rudin: Seções 4.1 a 4.4, páginas 83 a 90 e 93).
(23.4.25) Espaços métricos (xiv): conexidade (ii) – caracterização de desconexidade pela existência de subconjuntos próprios que são simultaneamente abertos e fechados na topologia relativa. Funções em espaços métricos (i): funções entre espaços métricos, funções contínuas num ponto, limites de funções com domínio num subconjunto de um espaço métrico num ponto de acumulação do domínio, caracterização de continuidade em pontos de acumulação em termos de limites. Unicidade do limite. Interlúdio: imagens e imagens inversas de funções, caracterização de sobrejetividade e injetividade em termos de imagens inversas, comportamento de uniões e intersecções com respeito a imagens inversas. Funções contínuas em (todos os pontos de) um espaço métrico: caracterização global (imagens inversas de abertos são abertas), imagens de subconjuntos compactos (resp. conexos) por funções contínuas são compactos (resp. conexos) (Rudin: Seções 4.1 a 4.4, páginas 83 a 89 e 93).
(16.4.25) Espaços métricos (xiii): conexidade (i) – definição de (des)conexidade em termos de subconjuntos separados e cisôes. Caracterização e classificação dos subconjuntos conexos ( = intervalos) dos reais (Rudin: Seção 2.5, páginas 42 e 43).
(11.4.25) Espaços métricos (xii): produtos cartesianos de espaços métricos (iv) – Teorema de Tychonoff (o produto cartesiano de dois espaços métricos compactos é compacto), prova em termos da propriedade de Bolzano-Weierstrass (ii). Interlúdio: caracterização de conjuntos infinitos em termos da existência de subconjuntos finitos com qualquer número de elementos, existência de subconjuntos infinitos e enumeráveis usando o Axioma da Escolha Enumerável.
(9.4.25) Espaços métricos (xi): produtos cartesianos de espaços métricos (iii) – recapitulação (distâncias equivalentes no produto cartesiano de dois espaços métricos). Teorema de Tychonoff (o produto cartesiano de dois espaços métricos compactos é compacto) – prova em termos da propriedade de Bolzano-Weierstrass (i).
(4.4.25) Espaços métricos (x): Produtos cartesianos de espaços métricos (ii) – distâncias no produto cartesiano, prova dos axiomas de distância. Interlúdio: desigualdade de Cauchy-Schwarz para o produto escalar em 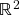$\mathbb{R}^2$ e desigualdade triangular para a norma euclideana em 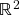$\mathbb{R}^2$ . Equivalência de distâncias, igualdade das topologias geradas por distâncias equivalentes. Teorema de Tychonoff (o produto cartesiano de dois espaços métricos compactos é compacto) – enunciado em termos da propriedade de Bolzano-Weierstrass.
(2.4.25) Espaços métricos (ix): compacidade (vi) – propriedade de Heine-Borel (recapitulação), caracterização da propriedade de Heine-Borel em termos da compacidade das bolas fechadas. Validade da propriedade de Heine-Borel para $\mathbb{R}$ (teorema de Heine-Borel): prova. Produtos cartesianos de espaços métricos (i): distâncias no produto cartesiano (Rudin: Seção 2.3, páginas 36 a 38).
(28.3.25) Espaços métricos (viii): compacidade (v) – caracterização pela propriedade de Bolzano-Weierstrass (iii). Espaços métricos satisfazendo a propriedade de Bolzano-Weierstrass são separáveis – prova (ii). Espaços métricos satisfazendo a propriedade de Bolzano-Weierstrass satisfazem a propriedade de Lindelöf (todo recobrimento aberto adminte um subrecobrimento enumerável), espaços métricos satisfazendo as propriedades de Bolzano-Wierstrass e de Lindelöf são compactos. Compacidade em $\mathbb{R}$ (i): subconjuntos limitados de um espaço métrico, propriedade de Heine-Borel (todo subconjunto fechado e limitado é compacto). Validade da propriedade de Heine-Borel para $\mathbb{R}$ (teorema de Heine-Borel) – enunciado. Lema dos intervalos encaixantes (Rudin: Seções 2.3 e 2.6, páginas 36 a 38 e 45).
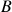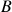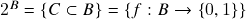(26.3.25) Interlúdio: conjuntos finitos e infinitos, conjuntos enumeráveis e não enumeráveis (iv) – teorema de Cantor-Bernstein (todo conjunto não-vazio $B$ admite uma função injetora de $B$ em $2^B=\{C\subset B\}=\{f:B\rightarrow\{0,1\}\}$ , mas tal função não pode ser sobrejetora). Espaços métricos (vii): compacidade (iv) – caracterização pela propriedade de Bolzano-Weierstrass (ii). Preliminares: bases (topológicas) de um espaço métrico, espaços métricos separáveis. Espaços métricos separáveis possuem uma base enumerável. Espaços métricos satisfazendo a propriedade de Bolzano-Weierstrass são separáveis – enunciado e prova (i) (Rudin: Seções 2.3 e 2.6, páginas 36 a 38 e 45).
(21.3.25) Interlúdio: conjuntos finitos e infinitos, conjuntos enumeráveis e não enumeráveis (iii). Recapitulação – definições, subconjuntos de conjuntos finitos (resp. enumeráveis) são finitos (resp. enumeráveis), $\mathbb{N}\times\mathbb{N}$ é enumerável, a união de uma família enumerável de conjuntos enumeráveis é enumerável. A união de dois conjuntos finitos é finita. 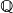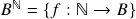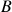Enumerabilidade de $\mathbb{Q}$ , não-enumerabilidade de $B^{\mathbb{N}}=\{f:\mathbb{N}\rightarrow B\}$ para $B$ finito e com pelo menos dois elementos (argumento diagonal de Cantor), não-enumerabilidade de $[0,1]$ e de $\mathbb{R}$ (Rudin: Seção 2.1, páginas 25, 26, 29 e 30).
(19.3.25) Interlúdio: conjuntos finitos e infinitos, conjuntos enumeráveis e não enumeráveis (ii). Recapitulação – definições, construção recursiva de enumerações de conjuntos enumeráveis. Subconjuntos de conjuntos finitos (resp. enumeráveis) são finitos (resp. enumeráveis). Provando que $\mathbb{N}\times\mathbb{N}$ é enumerável (enumeração triangular). Consequências da enumerabilidade de $\mathbb{N}\times\mathbb{N}$ : 1.) a união de uma família enumerável de conjuntos enumeráveis é enumerável (Rudin: Seção 2.1, páginas 25, 26, 29 e 30).
(14.3.25) Espaços métricos (vi): compacidade (iii) – recapitulação (definição de subconjuntos compactos). Propriedades de compactos (iii): recapitulação (subconjuntos finitos são compactos, compacidade é herdada por subespaços métricos, compactos são fechados, subconjuntos fechados de compactos são compactos, propriedade de intersecção finita, lema dos compactos encaixantes, propriedade de Bolzano-Weierstrass). Equivalência da propriedade de Bolzano -Weierstrass com compacidade (i): enunciado e preliminares – espaços métricos separáveis. Interlúdio: conjuntos finitos e infinitos, conjuntos enumeráveis e não enumeráveis (i) (Rudin: Seções 2.1 e 2.3, páginas 25, 26, 29, 30 e 36 a 38).
(12.3.25) Espaços métricos (v): compacidade (ii) – recapitulação (recobrimentos, recobrimentos abertos e finitos de um subconjunto de um espaço métrico, subrecobrimentos de um recobrimento, definição de subconjuntos compactos). Propriedades de compactos (ii): subconjuntos finitos são compactos, compacidade é herdada por subespaços métricos, compactos são fechados ( + interlúdio – propriedade de Hausdorff para espaços métricos), subconjuntos fechados de compactos são compactos, propriedade de intersecção finita, lema dos compactos encaixantes (corolário), propriedade de Bolzano-Weierstrass (subconjuntos infinitos de um compacto possuem pontos de acumulação nesse mesmo compacto) (Rudin: Seção 2.3, páginas 36 a 38).
(7.3.25) Espaços métricos (iv): pontos isolados e pontos de acumulação de um subconjunto de um espaço métrico – definição, classificação dos pontos do fecho de um subconjunto. Subconjuntos discretos e subconjuntos perfeitos – definição e exemplos. Subconjuntos densos. Compacidade (i): preliminares – recobrimentos, recobrimentos abertos e finitos de um subconjunto de um espaço métrico, subrecobrimentos de um recobrimento. Subconjuntos compactos – definição e propriedades (i) (Rudin: Seções 2.2 e 2.3, páginas 32, 36 e 37).
(28.6.25) Espaços métricos (iii): recapitulação – definição e axiomas de distância, desigualdade triangular reversa (enunciado e prova), bolas abertas, bolas fechadas e esferas num espaço métrico, bolas abertas (resp. fechadas) são abertas (resp. fechadas). O interior (resp. fecho) de um subconjunto é o maior (resp. menor) aberto (resp. fechado) contido em (resp. que contém) esse subconjunto e, equivalentemente, a união (resp. intersecção) dos abertos (resp. fechados) contidos em (res. que contém) esse subconjunto. Subconjuntos não-vazios de um espaço métrico como espaços métricos com a distância induzida: subconjuntos relativamente abertos e relativamente fechados com respeito a um subconjunto não-vazio – definição e caracterização. Interlúdio: o Axioma da Escolha (Rudin: Seção 2.2, páginas 30 a 35, Tao I: Seção 8.4, páginas 198 a 202).
(26.2.25) Espaços métricos (ii): recapitulação – definição e axiomas de distância, bolas abertas, bolas fechadas e esferas num espaço métrico, caracterização das bolas abertas (resp. fechadas) em $\mathbb{R}$ como intervalos abertos (resp. fechados), pontos interiores, exteriores e de fronteira de um subconjunto de um espaço métrico, exterior, interior e fronteira de um subcojunto de um espaço métrico. Subconjuntos não-vazios de um espaço métrico como espaços métricos com a distância induzida. Propriedades do interior e do fecho com respeito a complementos, inclusões, uniões e intersecções. Provando que bolas abertas (resp. fechadas) são abertas (resp. fechadas), desigualdade triangular reversa (enunciado) (Rudin: Seção 2.2, páginas 30 a 35).
(21.2.25) Espaços métricos (i): definição e axiomas de distância, bolas abertas, bolas fechadas e esferas num espaço métrico. $\mathbb{R}$ como espaço métrico: módulo ( = valor absoluto) num corpo ordenado – definição e propriedades, definição da distância em $\mathbb{R}$ em termos do módulo. Interlúdio: intervalos num conjunto ordenado. Caracterização das bolas abertas (resp. fechadas) em $\mathbb{R}$ como intervalos abertos (resp. fechados). Propriedades de espaços métricos (i): posição relativa de um ponto com respeito a um subconjunto – pontos interiores, exteriores e de fronteira, subconjuntos abertos e fechados. Axiomas de topologia para abertos e fechados, leis de de Morgan (Rudin: Seção 2.2, páginas 30 a 35).
(19.2.25) Preliminares (iii): caracterização axiomática dos reais (iii) – cotas superiores e inferiores, supremo e ínfimo de um subconjunto não-vazio de um conjunto ordenado, unicidade do supremo e do ínfimo. Conjuntos ordenados completos, propriedade do supremo e do ínfimo. O efeito da mudança de sinal sobre cotas superiores e inferiores em corpos ordenados, caracterização de corpos ordenados completos pela propriedade do supremo ou do ínfimo. Completeza dos reais como corpo ordenado e suas consequências: propriedade arquimedeana, densidade dos racionais nos reais (Rudin: Seções 1.2 e 1.3, páginas 3 a 9).
(14.2.25) Preliminares (ii): caracterização axiomática dos reais (ii) – recapitulação (estrutura de corpo, estrutura de ordem). Derivação das propriedades da ordem dos reais a partir das propriedades dos reais não-negativos. Inclusão dos naturais, inteiros e racionais nos reais, propriedade arquimedeana dos racionais e dos reais. Módulo ( = valor absoluto) de um número real: definição e propriedades, distância entre reais (estrutura de espaço métrico) (Rudin: seções 1.1 a 1.3, páginas 1 a 8).
(12.2.25) Informações sobre o funcionamento do curso. Análise real como fundamento conceitual do Cálculo diferencial (e integral = assunto de Análise Real II). Preliminares (i): sequências num conjunto – definição, termos de uma sequência, rearranjos e subsequências de uma sequência. Sequências estacionárias, recorrentes e periódicas. Preliminares (ii): caracterização axiomática dos reais (i) – estrutura de corpo, estrutura de ordem. (Rudin: seções 1.1 a 1.3, páginas 1 a 8)

Bibliografia

Listamos aqui os textos que seguiremos mais de perto.

Walter Rudin, Principles of Mathematical Analysis (3a. edição). McGraw-Hill, 1976.
Michael Spivak, Calculus (3a. edição). Publish or Perish, 1994;
Robert S. Strichartz, The Way of Analysis (ed. revisada). Jones and Bartlett, 2000;
Terence Tao, Analysis I, II (3a. edição). Hindustan Book Agency, 2014.

Textos suplementares:

Alfredo J. Aragona, Números Reais. Editora Livraria da Física, 2010;
Djairo G. de Figueiredo, Análise I (2a. edição). LTC Editora Ltda., 1996;
Chaim S. Hönig, Aplicações da Topologia à Análise. Editora Livraria da Física, 2011;
Elon L. Lima, Curso de Análise – Volume 1 (11a. edição). Projeto Euclides, IMPA, 2010.

Recomendações e material didático suplementar

Faremos uso tácito dos conceitos vistos nas disciplinas BCN0402 – Funções de uma Variável, BCN0405 – Introdução às Equações Diferenciais Ordinárias e MCBM007 – Números Reais e Sequências. No caso da última disciplina, conceitos básicos sobre sequências e a caracterização axiomática de $\mathbb{R}$ serão recapitulados brevemente e usados ao longo do curso.

Avaliação

Média preliminar:
M_p = média das listas de exercícios
Média final:
M_f = 0,5*(Rec+M_p)
Critério de conversão de média preliminar (M_p) / final (M_f) para conceito preliminar (C_p) / final (C_f): C_p (resp. C_f) = F – M_p (resp. M_f) < 4,5;
C_p (resp. C_f) = D – M_p (resp. M_f) = 4,5-5,2;
C_p (resp. C_f) = C – M_p (resp. M_f) = 5,3-6,9;
C_p (resp. C_f) = B – M_p (resp. M_f) = 7,0-8,4;
C_p (resp. Cf) = A – M_p (resp. M_f) = 8,5-10,0.

A prova de recuperação será aplicada no início do 2q’25, em data e local a serem divulgados futuramente. Apenas participantes que ficaram com conceitos preliminares D e F (ver critério acima) poderão fazer essa prova.

Listas de exercícios

A serem disponibilizadas em breve.

É extremamente importante que @s participantes façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!

Plantão de dúvidas

Haverá um plantão de dúvidas às sextas-feiras das 17h00 às 19h00, na minha sala (A-S543-2, Torre 2, Bloco A, campus Santo André). O plantão terá início no dia 14.2.

Finalmente, o Moodle terá um fórum aberto de perguntas e respostas onde @s participantes poderão tirar suas dúvidas assincronamente com o docente e/ou colegas.

Roteiro

Recapitulação: números reais e sequências, completeza e caracterização do corpo dos números reais.
Espaços métricos e sua topologia.
Limites de funções, funções contínuas.
Subconjuntos conexos, teorema do valor intermediário.
Compacidade, teoremas de Heine-Borel e Bolzano-Weierstrass.
Continuidade uniforme, teorema de Heine-Cantor.
Conjuntos de Cantor.
Diferenciabilidade e derivada.
Propriedades da derivada: teorema do valor médio e suas consequências, derivadas de ordem superior e polinômios de Taylor.
Aplicações da derivada, concavidade e convexidade.