
Este é o plano de ensino para a disciplina MCTB001 – Álgebra Linear (AlgLin) conforme ministrada no primeiro quadrimestre letivo de 2021 = segundo Quadrimestre Suplementar (QS) para as seguintes turmas:
- A2 – Noturno, campus Santo André – horário presencial: 3as. feiras e 4as. feiras 19h00-21h00, 6as. feiras 21h00-23h00.
- B2 – Noturno, campus Santo André – horário presencial: 3as. feiras e 4as. feiras 21h00-23h00, 6as. feiras 19h00-21h00.
Aqui encontram-se informações específicas sobre as turmas acima.
Novidades
Notícias recentes sobre o funcionamento do curso serão postadas aqui.
- (3.6.21) A janela temporal da prova de recuperação será aberta das 00h00 de terça-feira, 15.6 às 23h59 de quinta-feira, 17.6. Observo que a prova só estará acessível aos alunos com conceitos preliminares D e F. Haverá um plantão de dúvidas de recuperação por videoconferência (Google Meet) na quinta-feira, 10.6 das 16h00 às 19h00. O link para a sala de reunião será divulgado no máximo 30 minutos antes do início do plantão.
- (3.6.21) Os conceitos preliminares (Turma A2 Noturno SA, Turma B2 Noturno SA) estão disponíveis. Atentar para o fato que a planilha de conceitos de cada turma só está acessível para integrantes da mesma. Devido aos problemas técnicos que causaram o atraso no lançamento dos conceitos preliminares, as notas e correções das resoluções das Listas 3 a 6 demorarão mais alguns dias para serem disponibilizadas. Em virtude disso, poderá haver um ajuste na média das listas para beneficiar quem ficou com conceito preliminar D ou F e tem direito de fazer a prova de recuperação. As notas e correções das resoluções das Listas 1, 2 e 7 estão disponíveis no Moodle.
- (30.4.21) A janela de resolução para a prova substitutiva estará aberta das 10h00 da manhã de sábado, 8.5 às 9h59 da manhã de segunda-feira, 10.5. Tal prova deverá ocorrer nos mesmos moldes da P1 e da P2, mas varrerá todo o conteúdo de ambas as provas. Será concedido acesso à prova substitutiva apenas aos alunos que enviarem justificativa formal por escrito para a ausência na P1 ou P2 até as 8h59 da manhã de sábado, 8.5.
- (30.4.21) A matéria da P2 varrerá o conteúdo das Listas 5 a 8.
- (30.4.21) A Lista 8 está disponível.
- (13.4.21) A Lista 7 está disponível.
- (12.4.21) As Listas 5 e 6 estão disponíveis.
- (26.3.21) Conforme informe da Reitoria enviado ontem (quinta-feira, 25.3), os calendários acadêmico e administrativo da UFABC estão mantidos apesar da antecipação dos feriados municipais e a suspensão dos dias úteis no Grande ABC entre 27 de março e 04 de abril. Contudo, o mesmo informe e um comunicado posterior da Prograd enviado hoje (sexta-feira, 26.3) orienta a remarcação da entrega de atividades avaliativas para a partir de 5.4. Portanto, a janela temporal da P1 será remarcada para da 00h00 de terça-feira, 6.4 às 23h59 de quinta-feira, 8.4. Em virtude dessa remarcação, a transmissão das aulas e do plantão de dúvidas, bem como a gravação das primeiras, de 29.3 a 1.4 seguirão o horário normal, lembrando que haverá recesso na Sexta-Feira Santa, 2.4 (já presente no calendário acadêmico) e portanto não haverá transmissão ou gravação de aula nessa data.
- (25.3.21) A matéria da P1 varrerá o conteúdo das Listas 1 a 4.
- (12.3.21) As janelas das provas (P1, P2) e as janelas de envio de resoluções das Listas 1 a 4 foram fixadas. Ver a seção “Avaliação” abaixo para detalhes.
- (12.3.21) A Lista 4 está disponível.
- (22.2.21) As Listas 1, 2 e 3 estão disponíveis.
- (19.2.21) Venho aqui prestar um esclarecimento sobre o funcionamento da transmissão síncrona das aulas, realizada às 3as. e 6as. feiras das 19h00às 21h00, reforçando as informações já divulgadas neste plano de ensino. O horário de 3as. feiras corresponde ao da turma A2 noturno – campus Santo André, ao passo que o horário de 6as. feiras corresponde ao da turma B2 noturno – campus Santo André. Esse número de transmissões semanais (contando a transmissão do plantão de dúvidas às 5as. feiras das 18h00 às 21h00) visa permitir uma maior participação dos alunos nas aulas expositivas, dentro das condições de internet e das regras de condomínio de onde moro. Por causa disso, o controle de presença nas transmissões de aulas síncronas é semanal: basta que cada aluno compareça a pelo menos uma das transmissões na semana para que sua presença nas aulas daquela semana seja computada, de acordo com sua conveniência de horário. Observo também que, em virtude do caráter remoto das aulas nos Quadrimestres Suplementares, o controle de presença não será usado para fins de reprovação por falta.
- (15.2.21) De acordo com o calendário acadêmico de 2021, devido aos recessos nos dias 16 de fevereiro (terça-feira) e 17 de fevereiro (quarta-feira), não haverá aulas correspondentes a essas datas nesta semana. A reposição desses feriados será feita de acordo com o calendário de reposição oficial do primeiro quadrimestre letivo de 2021. As atividades do curso serão retomadas normalmente na quinta-feira, 18 de fevereiro. A aula 6, correspondente a 12 de fevereiro (sexta-feira), estará disponível até quinta-feira, 18 de fevereiro. As primeiras listas de exercícios estarão disponíveis até segunda-feira, 22 de fevereiro, a primeira versão das notas de aula estará disponível até sábado, 27 de fevereiro.
- (12.2.21) Devido ao atraso no cronograma de gravação das aulas provocado pela aula 4 (terça-feira, 9.2) ter precisado ser regravada, a aula 6 (hoje – sexta-feira, 12.2) será gravada normalmente mas não será transmitida sincronamente pelo Google Meet das 19h às 21h, dado que não haverá tempo hábil para assistir as aulas que a precedem – o vídeo da aula 4 já está disponivel mas o vídeo da aula 5 só estará disponível até o fim da data de hoje. O vídeo da aula 6, por sua vez, estará disponível até o final de amanhã (sábado, 13.2). A transmissão das aulas de terças-feiras e sextas-feiras voltará ao normal na semana que vem. Pelo mesmo motivo, as listas de exercícios e a primeira versão das notas de aula deverão estar disponíveis até segunda-feira, 15.2.
- (11.2.21) Os plantões de monitoria tiveram início nesta semana. Ver a seção “Monitoria, atendimento online e plantão de dúvidas” abaixo para os horários de atendimento no Google Meet. Informo que meus plantões de dúvidas às 5as. feiras das 18h00 às 21h00 continuarão normalmente.
- (6.2.21) Alguns alunos reportaram dúvidas sobre o procedimento para vincular o email institucional da UFABC à sua conta Google (Gmail, etc.). Esse procedimento é necessário (por razões de segurança e de controle de participação dos alunos) para acessar as salas de reunião do Google Meet usadas na transmissão síncrona das aulas de terça-feira e sexta-feira, bem como nos plantões de dúvidas. Para tal, recomendo seguir o tutorial do NTI. O link foi adicionado às orientações abaixo – ver seção “Estrutura das atividades da disciplina”.
Aulas
Os links para o material de cada aula (vídeo e blog), acompanhados de uma breve descrição desta, serão listados aqui.
- Aula 30 – 30.4.21 (vídeo) – Determinantes (III) – cálculo por eliminação gaussiana, autovalores e autovetores. Recapitulando: funções determinantes em
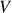 – definição e propriedades (
– definição e propriedades ( -linearidade, anti-simetria e sua equivalência com alternância sob
-linearidade, anti-simetria e sua equivalência com alternância sob  -linearidade). Expressão de uma função determinante pelo seu valor numa base ordenada, a função determinante associada a uma base ordenada.O determinante de uma t.l.: definição, independência da escolha de base ordenada e propriedades: (i) determinante de uma t.l. = determinante de sua adjunta (determinante de uma matriz = determinante da transposta); (ii) determinante do produto = produto dos determinantes; (iii) troca de colunas ou linhas troca o sinal do determinante; (iv) multiplicar uma coluna ou linha por um escalar multiplica o determinante pelo mesmo fator; (v) somar a uma coluna (resp. linha) uma c.l. das outras colunas (resp. linhas) não muda o determinante (corolário: se as linhas ou colunas forem l.d., o determinante é zero). (vi) o determinante da inversa é a recíproca do determinante (em particular, o determinante de uma t.l. invertível é diferente de zero). Aplicação das propriedades (ii)-(v) ao cálculo de determinantes por eliminação gaussiana. Autovalores e autovetores de uma t.l.: definição, equação de autovalor, autoespaços, o polinômio característico. T.l.’s diagonalizáveis, cálculo de autovalores e bases dos respectivos autoespaços.
-linearidade). Expressão de uma função determinante pelo seu valor numa base ordenada, a função determinante associada a uma base ordenada.O determinante de uma t.l.: definição, independência da escolha de base ordenada e propriedades: (i) determinante de uma t.l. = determinante de sua adjunta (determinante de uma matriz = determinante da transposta); (ii) determinante do produto = produto dos determinantes; (iii) troca de colunas ou linhas troca o sinal do determinante; (iv) multiplicar uma coluna ou linha por um escalar multiplica o determinante pelo mesmo fator; (v) somar a uma coluna (resp. linha) uma c.l. das outras colunas (resp. linhas) não muda o determinante (corolário: se as linhas ou colunas forem l.d., o determinante é zero). (vi) o determinante da inversa é a recíproca do determinante (em particular, o determinante de uma t.l. invertível é diferente de zero). Aplicação das propriedades (ii)-(v) ao cálculo de determinantes por eliminação gaussiana. Autovalores e autovetores de uma t.l.: definição, equação de autovalor, autoespaços, o polinômio característico. T.l.’s diagonalizáveis, cálculo de autovalores e bases dos respectivos autoespaços. - Aula 29 – 27.4.21 (vídeo) – Determinantes (II). Recapitulando: a
 -ésima potência cartesiana de um espaço vetorial
-ésima potência cartesiana de um espaço vetorial  -dimensional
-dimensional 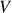 , bases ordenadas de
, bases ordenadas de 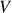 , funções determinantes em
, funções determinantes em 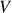 – definição e propriedades (
– definição e propriedades ( -linearidade, anti-simetria e sua equivalência com alternância sob
-linearidade, anti-simetria e sua equivalência com alternância sob  -linearidade). Expressão de uma função determinante pelo seu valor numa base ordenada, a função determinante associada a uma base ordenada. O determinante de uma t.l.: definição, independência da escolha de base ordenada e propriedades: (a) determinante de uma t.l. = determinante de sua matriz numa base qualquer; (b) determinante de uma t.l. = determinante de sua adjunta (determinante de uma matriz = determinante da transposta); (c) determinante do produto = produto dos determinantes; (d) uma t.l. é invertível se e somente se seu determinante não for zero.
-linearidade). Expressão de uma função determinante pelo seu valor numa base ordenada, a função determinante associada a uma base ordenada. O determinante de uma t.l.: definição, independência da escolha de base ordenada e propriedades: (a) determinante de uma t.l. = determinante de sua matriz numa base qualquer; (b) determinante de uma t.l. = determinante de sua adjunta (determinante de uma matriz = determinante da transposta); (c) determinante do produto = produto dos determinantes; (d) uma t.l. é invertível se e somente se seu determinante não for zero. - Aula 28 – 23.4.21 (vídeo) – Determinantes (I). Preliminares: a
 -ésima potência cartesiana de um espaço vetorial
-ésima potência cartesiana de um espaço vetorial  -dimensional
-dimensional 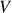 , bases ordenadas de
, bases ordenadas de 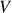 . Funções determinantes em
. Funções determinantes em 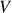 : definição e propriedades (
: definição e propriedades ( -linearidade, anti-simetria e sua equivalência com alternância sob
-linearidade, anti-simetria e sua equivalência com alternância sob  -linearidade). Interlúdio: permutações de
-linearidade). Interlúdio: permutações de  elementos – definição e exemplos (identidade, transposições e ciclos), o suporte de uma permutação, escrevendo permutações como um produto de transposições, o sinal de uma permutação.
elementos – definição e exemplos (identidade, transposições e ciclos), o suporte de uma permutação, escrevendo permutações como um produto de transposições, o sinal de uma permutação. - Aula 27 – 22.4.21 – em breve.
- Aula 26 – 20.4.21 (vídeo) – Sistemas lineares: o método de eliminação gaussiana e o método de Gauss-Jordan – consequências e aplicações (II). Recapitulação: Teorema do Núcleo e da Imagem e suas implicações: (a) uma t.l. é injetora se e somente se seu posto é igual à dimensão do domínio; (b) existência de uma t.l. bijetora implica igualdade das dimensões de seu domínio e contradomínio, cálculo de inversas de matrizes. Pseudoinversas – definição e propriedades, projeções associadas, redução à inversa no caso invertível. Cálculo da pseudoinversa com projeções associadas dadas.
- Aula 25 – 16.4.21 (vídeo) – Sistemas lineares: o método de eliminação gaussiana e o método de Gauss-Jordan – consequências e aplicações (I). Esquema conceitual do algoritmo de eliminação gaussiana. Construção de uma base da imagem de uma t.l. em termos de uma base de seu domínio, Teorema do Núcleo e da Imagem e suas implicações: (a) uma t.l. é injetora se e somente se seu posto é igual à dimensão do domínio; (b) existência de uma t.l. bijetora implica igualdade das dimensões de seu domínio e contradomínio. Cálculo de inversas de matrizes, cálculo de pseudoinversas de matrizes (esboço).
- Aula 24 – 14.4.21 (vídeo) – Sistemas lineares: o método de eliminação gaussiana e o método de Gauss-Jordan – exemplos de resolução de (i) sistemas lineares com solução única, (ii) sistemas lineares com solução não-única (princípio de superposição: solução geral = solução particular + solução geral do sistema linear homogêneo associado = solução particular + c.l. arbitrária de elementos de uma base de soluções do sistema linear homogêneo associado), (iii) e (iv) sistemas lineares sem solução.
- Aula 23 – 13.4.21 (vídeo) – Sistemas lineares: o método de eliminação gaussiana e o método de Gauss-Jordan. Recapitulação do método de eliminação gaussiana, critério de existência de soluções. O método de Gauss-Jordan como uma maneira de automatizar a substituição de variáveis resolvidas após eliminação gaussiana. Prescrição para encontrar uma solução particular de um sistema linear e um conjunto l.i. de soluções do sistema linear homogêneo associado. Provando que o conjunto l.i. encontrado de soluções do sistema linear homogêneo associado é uma base do espaço de soluções do mesmo: o Teorema do Núcleo e da Imagem.
- Aula 22 – 30.3.21 (vídeo) – Sistemas lineares: operações elementares e o método de eliminação gaussiana. Recapitulação: solução geral de sistemas lineares, forma matricial (variáveis e equações), operações elementares : (a) permutação de linhas; (b) multiplicação de uma linha por um escalar diferente de zero; (c) soma de um múltiplo escalar de uma linha a outra linha. Descrição e objetivo do algoritmo: matriz em forma escalonada (em linhas). Consequências elementares do algoritmo de eliminação gaussiana, critério de existência de soluções.
- Aula 21 – 26.3.21 (vídeo) – Sistemas lineares: operações elementares e o método de eliminação gaussiana. Recapitulação: definição abstrata de sistemas lineares, imagem e imagem inversa de uma t.l., núcleo e imagem de uma t.l.. Princípio de superposição, solução geral de sistemas lineares homogêneos, base de soluções. Solução geral de um sistema linear (possivelmente) não-homogêneo = solução particular + solução geral do sistema (linear) homogêneo associado ( = c.l. de soluções que formam uma base do núcleo). Forma matricial de um sistema linear – variáveis e equações. Sistemas lineares equivalentes: t.l.’s invertíveis e sua caracterização pela sua ação em uma base ( = a imagem é uma base). Operações elementares : (a) permutação de linhas; (b) multiplicação de uma linha por um escalar diferente de zero; (c) soma de um múltiplo escalar de uma linha a outra linha.
- Aula 20 – 23.3.21 (vídeo) – Sistemas lineares: definição abstrata e relação com a forma usual, variáveis e equações. Exemplos recorrentes em Álgebra Linear: (a) cálculo de componentes de um vetor numa base (sistema linear com uma única solução), (b) verificação de (in)dependência linear de um conjunto finito de vetores (sistema linear homogêneo) e sua conexão com a unicidade da solução (l.i. = solução única é zero; l.d. = existe solução não-zero = solução não é única), (c) possibilidade de expressar um vetor como c.l. de outros = sistema linear “genérico”. O espaço de soluções de um sistema linear: caso homogêneo (núcleo de uma t.l. – subespaço vetorial do domínio) e não-homogêneo (solução geral do sistema não-homogêneo = solução particular do mesmo + solução geral do sistema homogêneo associado). Existência de soluções = lado direito na imagem da t.l., unicidade de soluções e a dimensão do núcleo da t.l.. A ação de t.l.’s invertíveis sobre um sistema linear, sistemas lineares equivalentes.
- Aula 19 – 22.3.21 (vídeo) – A matriz de uma transformação linear (conclusão): o efeito de mudanças de base no domínio e contradomínio de uma t.l. sobre a sua matriz nesse par de bases. A matriz de mudança de base: definição e propriedades. Expressão das componentes de um vetor na base “nova” em termos das componentes na base “velha” e da (inversa da) matriz de mudança de base. Lei de transformação de matrizes de uma t.l. mediante mudança de bases em termos das entradas e em termos de vetores-coluna. O caso de bases o.n. – matrizes ortogonais e t.l.’s ortogonais.
- Aula 18 – 19.3.21 (vídeo) – A matriz de uma transformação linear (continuação): recapitulação – relação entre operações sobre t.l’s (soma, multiplicação escalar, produto = composição, adjunta, inversão) e operações matriciais (soma matricial, multiplicação escalar, produto matricial, transposta, inversão matricial). O efeito da mudança de bases no domínio e no contradomínio sobre a matriz de uma t.l..
- Aula 17 – 16.3.21 (vídeo) – A matriz de uma transformação linear (continuação): recapitulação – relação entre operações sobre t.l’s (soma, multiplicação escalar, produto = composição) e operações matriciais (soma matricial, multiplicação escalar, produto matricial). A adjunta de uma t.l. (com respeito a um par de produtos escalares no domínio e contradomínio) e sua relação com a transposta de uma matriz. Inversão de t.l.’s e inversão de matrizes, a matriz identidade.
- Aula 16 – 12.3.21 (vídeo) – A matriz de uma transformação linear: definição (recapitulação), o vetor-coluna ( = matriz com uma coluna) de um vetor numa base, a ação de uma t.l. como multiplicação de sua matriz num par de bases (no domínio e no contradomínio) por vetores-coluna na base do domínio. Expressão de uma t.l. em termos de um produto escalar no domínio. Funcionais lineares ( = 1-formas), o dual de um espaço vetorial (contradomínio =
 ): correspondência biunívoca de um espaço vetorial e seu dual (lema de Riesz), o vetor-linha de um funcional linear numa base do domínio, o produto escalar como produto de vetores-linha com vetores-coluna. Expressão de operações sobre t.l.’s como operações matriciais: soma, multiplicação escalar e produto.
): correspondência biunívoca de um espaço vetorial e seu dual (lema de Riesz), o vetor-linha de um funcional linear numa base do domínio, o produto escalar como produto de vetores-linha com vetores-coluna. Expressão de operações sobre t.l.’s como operações matriciais: soma, multiplicação escalar e produto. - Aula 15 – 10.3.21 (vídeo) – Transformações lineares (continuação): recapitulação – definição, axiomas e notação, o espaço de t.l.’s entre dois espaços vetoriais como um espaço vetorial. Produto ( = composição) e inversão de t.l.’s como t.l.’s. Distributividade, associatividade (prova) e não-comutatividade (enunciado) do produto de t.l.’s. A expressão de t.l.’s em termos de bases no domínio e no contradomínio, vetores-coluna, a matriz de uma transformação linear num par de bases no domínio e no contradomínio.
- Aula 14 – 9.3.21 (vídeo) – Transformações lineares (t.l.’s): definição e axiomas, propriedades básicas (preservação de combinações lineares e do vetor zero) e (contra)exemplos – aplicação zero, aplicações constantes, identidade num espaço vetorial, soma de uma t.l. com um vetor fixo no contradomínio (transformação afim), produto escalar com um vetor fixo, forma geral de uma t.l. com domínio de dimensão finita (enunciado), derivada (em espaços de funções continuamente diferenciáveis e de polinômios), lista ordenada de componentes de um vetor numa base. O espaço de t.l.’s entre dois espaços vetoriais como um espaço vetorial.
- Aula 13 – 5.3.21 (vídeo) – Ortonormalização de conjuntos l.i.: o método de Gram-Schmidt (parte 2 de 2). Recapitulação: projeções ortogonais ao longo de um subespaço vetorial – definição em termos de uma base ortonormal, propriedades (linearidade, ação no subespaço como a identidade deste, idempotência, ortogonalidade), projeção ortogonal de um vetor ao longo de um subespaço vetorial como o vetor mais próximo nesse subespaço. Algoritmo de Gram-Schmidt: construção, significado e exemplo de aplicação.
- Aula 12 – 3.3.21 (vídeo) – Projeções ortogonais: motivação (exemplo unidimensional, expansão de um vetor numa base ortonormal). A projeção ortogonal ao longo de um subespaço vetorial: definição em termos de uma base ortonormal. Propriedades de projeções ortogonais: vetor no subespaço com a menor distância = independência da escolha de base ortonormal, linearidade, ortogonalidade da projeção ortogonal de um vetor e da diferença entre ambos (teorema de Pitágoras). Ortonormalização de conjuntos l.i.: o método de Gram-Schmidt (parte 1 de 2).
- Aula 11 – 2.3.21 (vídeo) – Geometria do produto escalar. Recapitulação: definição, axiomas e exemplos (dimensão finita) de produtos escalares, conjuntos ortogonais e ortonormais, bases ortonormais. Distância euclidiana e ângulo euclidiano, a desigualdade de Cauchy-Schwarz: prova e consequências (definição de ângulo euclidiano faz sentido, desigualdade triangular para a norma euclidiana). Propriedades da norma euclidiana: axiomas de norma e de distância. Propriedades do ângulo euclidiano: ortogonalidade e dependência linear. Fórmula para as componentes de um vetor numa base ortonormal e sua interpretação geométrica, teorema de Pitágoras.
- Aula 10 – 26.2.21 (vídeo) – Produtos escalares. Motivação: produto escalar canônico em
 . Definição geral e axiomas. Exemplos (produto escalar canônico em
. Definição geral e axiomas. Exemplos (produto escalar canônico em  , espaços de funções contínuas). O produto escalar associado a uma base finita. Conjuntos ortogonais e ortonormais, bases ortonormais. O produto escalar associado a uma base finita como o único produto escalar com respeito ao qual tal base é ortonormal.
, espaços de funções contínuas). O produto escalar associado a uma base finita. Conjuntos ortogonais e ortonormais, bases ortonormais. O produto escalar associado a uma base finita como o único produto escalar com respeito ao qual tal base é ortonormal. - Aula 9 – 24.2.21 (vídeo) – Bases e dimensão de um espaço vetorial (conclusão). Recapitulação: definição de bases, componentes de um vetor ao longo de um elemento de uma base, representação das operações vetoriais em termos de componentes, identificação do espaço vetorial com um subespaço de funções da base a valores reais. Dimensão de um espaço vetorial: recapitulação de resultados estruturais preparatórios e definição. Exemplos (
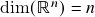 , espaços de funções com domínio infinito tem dimensão infinita). Critério dimensional para um conjunto l.i. ser uma base. Construção de bases num espaço vetorial de dimensão finita.
, espaços de funções com domínio infinito tem dimensão infinita). Critério dimensional para um conjunto l.i. ser uma base. Construção de bases num espaço vetorial de dimensão finita. - Aula 8 – 23.2.21 (vídeo) – Bases de um espaço vetorial. Recapitulação de (in)dependência linear. Bases: definição, componentes de um vetor ao longo de um elemento da base como “coordenadas lineares”, representação das operações vetoriais em termos das componentes de uma base, (contra)exemplos (base canônica de
 , espaços de funções). Bases finitas e dimensão de um espaço vetorial: resultados estruturais e definição (número de elementos de uma base finita = número de “coordenadas lineares”).
, espaços de funções). Bases finitas e dimensão de um espaço vetorial: resultados estruturais e definição (número de elementos de uma base finita = número de “coordenadas lineares”). - Aula 7 – 19.2.21 (vídeo) – (In)dependência linear: propriedades e intepretação (recapitulação), exemplos de conjuntos linearmente independentes (l.i.) em
 (base canônica) e em espaços de funções. O subespaço vetorial gerado por um subconjunto de um espaço vetorial: definição e caracterização (por que é um subespaço vetorial?). Bases de um espaço vetorial: definição.
(base canônica) e em espaços de funções. O subespaço vetorial gerado por um subconjunto de um espaço vetorial: definição e caracterização (por que é um subespaço vetorial?). Bases de um espaço vetorial: definição. - Aula 6 – 12.2.21 (vídeo) – Somatória vetorial: definição e propriedades. Combinações lineares: definição. Coeficientes de combinações lineares como “coordenadas lineares” num espaço vetorial. (In)dependência linear: definição e exemplos simples. Interpretação de dependência linear como “não unicidade” de “coordenadas lineares”.
- Aula 5 – 10.2.21 (vídeo) – Subespaços vetoriais – definição e caracterização. (Contra)exemplos: subespaço trivial, subespaços vetoriais de
 , espaços de polinômios, espaços de soluções de sistemas lineares homogêneos e não-homogêneos.
, espaços de polinômios, espaços de soluções de sistemas lineares homogêneos e não-homogêneos. - Aula 4 – 9.2.21 (vídeo) – Espaços vetoriais – exemplos:
 , espaços de funções a valores em
, espaços de funções a valores em  e num espaço vetorial
e num espaço vetorial 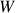 (caso particular:
(caso particular:  = domínio
= domínio  , contradomínio
, contradomínio  ) – definição, operações vetoriais, verificação dos axiomas de espaço vetorial. Subespaços vetoriais: definição.
) – definição, operações vetoriais, verificação dos axiomas de espaço vetorial. Subespaços vetoriais: definição. - Aula 3 – 5.2.21 (vídeo) – Espaços vetoriais (reais): definição, operações vetoriais (soma vetorial, multiplicação escalar) e axiomas de espaço vetorial. Consequências dos axiomas. Exemplos:
 , espaços de funções a valores em
, espaços de funções a valores em  (caso particular:
(caso particular:  = domínio
= domínio  ) – definição, operações vetoriais, verificação dos axiomas de espaço vetorial relativos à soma vetorial.
) – definição, operações vetoriais, verificação dos axiomas de espaço vetorial relativos à soma vetorial. - Aula 2 – 3.2.21 (vídeo) – Motivação (continuação): vetores de deslocamento num espaço de pontos (espaço afim). Derivação dos axiomas da soma vetorial e da multiplicação escalar para escalares inteiros e racionais.
- Aula 1 – 2.2.21 (vídeo) – informações sobre o funcionamento do curso. Motivação: o que são espaços vetoriais e qual a sua importância? Origem geométrica: vetores de deslocamento num espaço de pontos (espaço afim). Soma vetorial e seus axiomas. Multiplicação por escalares = fatores de escala naturais, inteiros e racionais.
Bibliografia
Listamos aqui os textos que seguiremos mais de perto.
- Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969. Uma versão online gratuita dos dois volumes em inglês pode ser encontrada aqui).
- Notas de aula serão disponibilizadas aqui à medida que o conteúdo for apresentado.
(Observação: o link do livro disponibilizado acima parte de um servidor que, em princípio, oferece tais materiais legalmente. Se for comprovado que este não é o caso, os links serão retirados sem aviso prévio)
A lista abaixo indica textos suplementares que podem ser de utilidade para o aluno.
- Notas de aulas do Prof. Jerônimo C. Pellegrini (atualizadas periodicamente).
- Howard Anton, Chris Rorres, Álgebra Linear com Aplicações (décima edição). Bookman, 2012 (original em inglês: Linear Algebra with Applications – 9th Edition. Wiley, 2005).
- G. Strang, Introduction to Linear Algebra (5a. edição). Wellesley Cambridge Press, 2016.
Recomendações e material didático suplementar
É recomendado que o aluno tenha cursado anteriormente a disciplina BCN0404 – Geometria Analítica. Ocasionalmente, conceitos básicos da disciplina BCN0402 – Funções de Uma Variável – e.g. cálculo de integrais simples – podem ser empregados em exemplos.
Estrutura das atividades da disciplina
As aulas terão inicialmente, em caráter experimental, um formato híbrido – serão disponibilizadas assincronamente três aulas por semana (menos o número de dias de feriado na semana em questão coincidindo com os dias do horário presencial) de acordo com a carga didática da disciplina, sendo que duas delas serão também transmitidas sincronamente nas seguintes datas e horários (exceto feriados – estes serão repostos no período de reposição seguindo o calendário acadêmico de 2021):
- Terças-feiras, 19h00-21h00;
- Sextas-feiras, 19h00-21h00.
Reitero que a transmissão das aulas síncronas será gravada e disponibilizada posteriormente de maneira assíncrona. O link para a sala de reunião (Google Meet) onde cada aula será transmitida será divulgado por email e pelo Moodle com no máximo 30 minutos de antecedência por razões de segurança. A entrada nas salas de reunião a partir de 5.2 só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de segurança e controle da participação dos alunos. Para realizar o vinculamento, recomendo seguir o tutorial do NTI para o procedimento.
As datas e horários acima foram escolhidas em função dos horários presenciais de cada turma – notar que o horário das terças-feiras corresponde ao da turma A2, enquanto que o horário das sextas-feiras corresponde ao da turma B2. O objetivo das aulas síncronas é permitir (dentro das limitações da internet de cada aluno e do docente) uma maior participação dos alunos. A depender da viabilidade desse formato expositivo na prática, ele será mantido ou poderá ter a parte síncrona reduzida ou mesmo removida – a avaliar.
Os links para o vídeo e a postagem de blog correspondentes a cada aula serão disponibilizados na lista de aulas.
Avaliação
A avaliação consistirá em dois tipos de atividades:
- Duas provas (P1, P2) a serem aplicadas na plataforma Moodle, no seguinte formato: haverá uma janela temporal de 72 horas para a prova ser feita. Uma vez iniciada dentro desse período, o aluno terá até 3 horas para enviar a resolução (período suficiente para lidar com eventuais dificuldades no envio).
- Envio de resoluções de seleções de exercícios para cada uma das listas de exercícios (ver a seção “Listas de exercícios” abaixo para mais detalhes). As resoluções correspondentes a cada lista deverão também ser enviadas pelo Moodle dentro de uma janela temporal de 72 horas.
Haverá uma prova de recuperação a ser agendada para o início do segundo quadrimestre letivo de 2021, no mesmo formato que a P1 e a P2 mas que cobrirá o conteúdo do curso inteiro.
Média preliminar: Mp = 0,25*(P1+P2) + 0,5*Ml , onde Ml é a média simples das resoluções das listas de exercícios.
Média final: Mf = 0,25*max(P1+P2 ,Rec+P1, Rec+P2) + 0,5*Ml
Critério de conversão de média preliminar (Mp) / final (Mf) para conceito preliminar (Cp) / final (Cf):
Cp (resp. Cf) = F – Mp (resp. Mf) < 4,5;
Cp (resp. Cf) = D – Mp (resp. Mf) = 4,5-5,2;
Cp (resp. Cf) = C – Mp (resp. Mf) = 5,3-6,9;
Cp (resp. Cf) = B – Mp (resp. Mf) = 7,0-8,4;
Cp (resp. Cf) = A – Mp (resp. Mf) = 8,5-10,0.
Sugestões de ferramentas gratuitas para digitalização de documentos em formato PDF usando a câmera de smartphones:
- Adobe Scan (Android, iOS);
- vFlat (somente para Android);
- Microsoft Office Lens (Android, iOS);
- Google Drive (ferramenta de digitalização integrada à nuvem da Google – aviso: esse recurso é mais limitado que o dos apps dedicados listados acima! Somente para Android).
Janelas das provas:
- P1 – 00h00 de terça-feira, 6.4 às 23h59 de quinta-feira, 8.4;
- P2 – 00h00 de quarta-feira, 5.5 às 23h59 de sexta-feira, 7.5;
- Sub – 10h00 de sábado, 8.5 às 9h59 de terça-feira, 11.5 (acessível apenas a alunos que apresentarem justificativa formal por escrito para a ausência na P1 ou P2);
- Rec – a ser agendada no início do segundo quadrimestre letivo de 2021.
Janelas de envio de resoluções das listas de exercícios:
- Listas 1 e 2 – 00h00 de terça-feira, 16.3 às 23h59 de quinta-feira, 18.3
- Listas 3 e 4 – 00h00 de terça-feira, 23.3 às 23h59 de quinta-feira, 25.3;
- Listas 5 e 6 – 00h00 de terça-feira, 20.4 às 23h59 de quinta-feira, 22.4;
- Lista 7 – 00h00 de terça-feira, 27.4 às 23h59 de quinta-feira, 29.4.
Durante cada janela de envio de resoluções de listas de exercícios, será aberta uma tarefa no Moodle com essa finalidade. Os detalhes sobre o envio das resoluções e as seleções de exercícios a serem resolvidos serão divulgados no início de cada janela.
Listas de exercícios
É extremamente importante que os alunos façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!
Monitoria, atendimento online e plantão de dúvidas
Haverá um plantão de dúvidas em videoconferência às quintas-feiras das 18h00 às 21h00, usando a plataforma Google Meet, tal como a transmissão síncrona das aulas.
O plantão terá início em caráter experimental no dia 4.2 – por razões de segurança, o link para a sala de reunião será divulgado por email e pelo Moodle no máximo 30 minutos antes do início de cada reunião.
Tal como na transmissão síncrona das aulas, a entrada nas salas de reunião dos plantões só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de controle da participação dos alunos.
Horários dos plantões de monitoria (início: 9.2 – por razões de segurança, os links para as salas de reunião do Google Meet onde o atendimento será feito devem ser acessados pelo Moodle):
- Ana Suelen Fernandes Gomes – 2as. feiras 10h-11h, 5as. feiras 19h-21h, 6as.feiras 18h-20h
- Daniel Saggiomo de Caprio – 3as. feiras 10h-12h e 18h-19h, 6as. feiras 10h-12h
- Diego Frizo – 2as. e 4as. feiras 19h-21h
Controle de frequência
A frequência será controlada mediante a participação nas aulas síncronas e nos plantões de dúvidas, bem como pela entrega das resoluções das seleções de exercícios das listas. A contabilização de presença nas transmissões síncronas das aulas será semanal – basta que o aluno compareça a uma aula síncrona da semana para que sua presença nas aulas daquela semana seja computada. Observo que, em virtude do caráter remoto das aulas, o controle de frequência não será usado para fins de reprovação por falta.
Roteiro
Seguiremos de maneira aproximada o cronograma sugerido para o curso de AlgLin pelo Gradmat, com algumas modificações na ordem e na ênfase – para uma descrição mais detalhada dos tópicos de cada aula, confira a lista das aulas. Uma descrição sucinta dos tópicos do curso na ordem a ser seguida pode ser vista abaixo.
- Espaços vetoriais: motivação, definição e exemplos (Anton-Rorres: seção 5.1; Apostol: seções 1.1 a 1.5; notas do Pellegrini: seção 1.4).
- Subespaços vetoriais: definição e exemplos (Anton-Rorres: seção 5.2; Apostol: seção 1.6; notas do Pellegrini: seção 1.5).
- Combinações lineares, dependência linear e independência linear. Subespaços vetoriais gerados por um conjunto de vetores (Anton-Rorres: seções 5.2 e 5.3; Apostol: seções 1.6 e 1.7; notas do Pellegrini: seção 2.1).
- Bases
e dimensão de um (sub)espaço vetorial, componentes de um vetor numa
base. Mudança de base (Anton-Rorres: seção 5.4; Apostol: seções 1.8 a
1.10; notas do Pellegrini: seções 2.2 e 2.4).
- Produtos escalares: definição e propriedades. Geometria do produto escalar: a desigualdade de Cauchy-Schwarz.
- Projeções ortogonais, bases ortogonais e ortonormais. Ortonormalização de Gram-Schmidt.
- Transformações lineares: definição e exemplos. A adjunta de uma transformação linear com respeito a um produto escalar.
- A
matriz de uma transformação linear numa base. O efeito da mudança de
base na matriz de uma transformação linear, matrizes de mudança de base.
- Núcleo e imagem de uma transformação linear. Posto e nulidade.
- Sistemas lineares, transformações lineares e matrizes. Operações elementares e escalonamento de matrizes: algoritmos de eliminação Gaussiana e de Gauss-Jordan.
- O determinante de uma transformação linear e de uma matriz.
- Autovalores e autovetores: definição e interpretação geométrica. O polinômio característico.
- Bases de autovetores e diagonalização de transformações lineares.
- Tópicos suplementares (se houver tempo): decomposição em valores singulares e a pseudoinversa de uma transformação linear, aplicações (mínimos quadrados, análise de componentes principais).

