

Este é o plano de ensino para a disciplina MCTB001 – Álgebra Linear (AlgLin) conforme ministrada no terceiro quadrimestre letivo de 2021 = quarto Quadrimestre Suplementar (QS) para a turma B1 – Noturno, campus Santo André – horário presencial: 3as. feiras e 4as. feiras 21h00-23h00, 6as. feiras 19h00-21h00.
Aqui encontram-se informações específicas sobre as turmas acima.
Novidades
Notícias recentes sobre o funcionamento do curso serão postadas aqui.
- (22.9.21) A primeira versão das notas de aula está disponível. Estas serão atualizadas gradativamente.
Aulas
Os links para o material de cada aula (vídeo e blog), acompanhados de uma breve descrição desta, serão listados aqui.
- Aula 31 – 10.12.21 (vídeo) – Autovalores e autovetores de uma transformação linear (ii): sumário – definição de autovalor, autovetor e autoespaço de uma transformação linear, o polinômio característico de uma transformação linear, autovalores = raízes reais do polinômio característico, diagonalização e diagonalizabilidade de uma transformação linear, bases de autovetores, independência linear de autovetores com autovalores distintos, critério de multiplicidades geométricas para diagonalizabilidade de uma transformação linear, o caso de transformações lineares simétricas com respeito a um produto escalar (condição necessária e suficiente, ortogonalidade de autovalores com autovalores distintos, bases ortonormais diagonalizantes). Algoritmo de diagonalização de uma transformação linear: (1) cálculo do polinômio característico e suas raízes reais; (2) cálculo de uma base de soluções para cada equação de autovalor. Exemplos, observações e ressalvas sobre o uso de eliminação gaussiana no algoritmo de diagonalização, os casos de autovalores distintos e de matrizes simétricas. Interpretação geométrica da (não) diagonalizabilidade de uma transformação linear. Coda: a decomposição em valores singulares de uma transformação linear e seu uso no cálculo da pseudoinversa de Moore-Penrose.
- Aula 30 – 8.12.21 (vídeo) – Autovalores e autovetores de uma transformação linear: definição de autovalor, autovetor e autoespaço de uma transformação linear. O polinômio característico de uma transformação linear, autovalores = raízes reais do polinômio característico. As multiplicidades algébrica ( = multiplicidade como raiz do polinômio característico) e geométrica ( = dimensão do autoespaço correspondente) de um autovalor. Diagonalização e diagonalizabilidade de uma transformação linear, bases de autovetores, independência linear de autovetores com autovalores distintos, critério de multiplicidades geométricas para diagonalizabilidade de uma transformação linear. Exemplos de transformações lineares não-diagonalizáveis: (1) uma transformação linear sem autovalores ( = sem raízes reais no polinômio característico); (2) uma transformação linear diferente de zero cujo único autovalor é zero. O caso de transformações lineares simétricas com respeito a um produto escalar (condição necessária e suficiente) – ortogonalidade de autovalores com autovalores distintos, bases ortonormais diagonalizantes.
- Aula 29 – 7.12.21 (vídeo) – Determinantes (iv): sumário de resultados – definição e propriedades de funções determinantes, determinação de uma função determinante por seu valor numa base ordenada, função determinante associada a uma base ordenada, determinante de uma transformação linear (definição e propriedades). Determinantes de matrizes: expressão de propriedades em termos de colunas e linhas, expressão do critério do determinante para invertibilidade de matrizes na linguagem de sistemas lineares, regra de Cramer. Cálculo de determinantes por eliminação gaussiana: determinantes de operações elementares e seu efeito sobre o escalonamento de uma matriz, determinante da matriz escalonada em termos do critério do posto. Exemplos de cálculo de determinantes por eliminação gaussiana, comparação com o cálculo pela definição.
- Aula 28 – 3.12.21 (vídeo) – Determinantes (iii): recapitulação – definição e propriedades de funções determinantes, determinação de uma função determinante por seu valor numa base ordenada. A função determinante associada a uma base ordenada. O determinante de uma transformação linear: definição em termos da função determinante associada a uma base ordenada e sua independência da escolha dessa base. Propriedades do determinante: relação com determinantes de matrizes, invariância por transposição, propriedade do produto, critério do determinante para invertibilidade de transformações lineares e matrizes.
- Aula 27 – 1.12.21 (vídeo) – Determinantes (ii):
 -formas num espaço vetorial – definição, caracterização da propriedade de anti-simetria de uma
-formas num espaço vetorial – definição, caracterização da propriedade de anti-simetria de uma  -forma, determinação de uma
-forma, determinação de uma  -forma por seus valores na
-forma por seus valores na  -ésima potência cartesiana de uma base. Funções determinantes num espaço vetorial
-ésima potência cartesiana de uma base. Funções determinantes num espaço vetorial 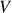 ( =
( =  -formas em
-formas em 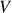 com
com 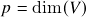 ). Interlúdio: permutações – definição, estrutura de grupo, sinal de uma permutação e propriedades do mesmo, transposições, seu sinal e decomposição de uma permutação como um produto de transposições (enunciado). Bases ordenadas de um espaço vetorial, determinação de uma função determinante por seu valor numa base ordenada.
). Interlúdio: permutações – definição, estrutura de grupo, sinal de uma permutação e propriedades do mesmo, transposições, seu sinal e decomposição de uma permutação como um produto de transposições (enunciado). Bases ordenadas de um espaço vetorial, determinação de uma função determinante por seu valor numa base ordenada. - Aula 26 – 30.11.21 (vídeo) – Sistemas lineares (v): aplicação de eliminação gaussiana à determinação da invertibilidade de uma matriz pelo critério do posto (número de pivôs da matriz escalonada = número de colunas = número de linhas) e ao cálculo da inversa (se existir) – exemplo. Determinantes de transformações lineares e de matrizes (i): motivação geométrica em duas e três dimensões – paralelepípedos gerados por vetores e seus volumes, fórmula de Lagrange, a matriz de Gram. A ação de transformações lineares sobre um cubo bi- e tridimensional e seu efeito sobre o volume. Funções determinantes: definição.
- Aula 25 – 26.11.21 (vídeo) – Sistemas lineares (iv): exemplos concretos de aplicação do algoritmo de eliminação Gaussiana ( = escalonamento de matrizes) e do algoritmo de Gausss-Jordan – 1.) sistemas lineares com uma única solução; 2.) sistemas lineares com mais de uma solução (cálculo da solução geral); 3.) sistemas lineares sem solução. Aplicação de eliminação gaussiana à determinação da invertibilidade de uma matriz pelo critério do posto (número de pivôs da matriz escalonada = número de colunas = número de linhas) e ao cálculo da inversa (se existir).
- Aula 24 – 24.11.21 (vídeo) – Sistemas lineares (iii): eliminação gaussiana e de Gauss-Jordan. Recapitulação: objetivo e descrição do algoritmo de eliminação gaussiana, obtenção de uma solução particular de um sistema escalonado como combinação linear de colunas nos pivôs da matriz escalonada. O algoritmo de Gauss-Jordan. A solução particular do sistema escalonado como uma pseudoinversa. Obtenção de uma base de soluções do sistema linear homogêneo associado.
- Aula 23 – 23.11.21 (vídeo) – Sistemas lineares (ii): recapitulação – (a) forma abstrata, soluções, sistemas homogêneos e não-homogêneos, o sistema linear homogêneo associado a um sistema linear não-homogêneo, critério de existência e unicidade de soluções, princípio de superposição; (b) sistemas lineares em forma matricial, equações e variáveis de um sistema linear, a matriz aumentada de um sistema linear. O método de eliminação gaussiana (escalonamento de matrizes): revisão de fundamentos conceituais, matrizes escalonadas em linhas e seus pivôs. Solução particular de um sistema linear a partir do escalonamento de sua matriz num par de bases. Descrição do algoritmo de eliminação gaussiana e sua eficácia.
- Aula 22 – 19.11.21 (vídeo) – Sistemas lineares: forma abstrata, soluções, sistemas homogêneos e não-homogêneos, o sistema linear homogêneo associado a um sistema linear não-homogêneo. Sistemas lineares em forma matricial, equações e variáveis de um sistema linear. Critério de existência e unicidade de soluções, princípio de superposição. O método de eliminação gaussiana (escalonamento de matrizes): fundamentos conceituais – operações elementares, matrizes escalonadas em linhas e seus pivôs. Refinamento do critério de existência e unicidade de soluções de sistemas lineares por meio de eliminação gaussiana.
- Aula 21 – 17.11.21 (vídeo) – Pseudoinversas de transformações lineares (ii): recapitulação – definição e propriedades, projeções no domínio e no contradomínio associadas a uma pseudoinversa, ambiguidade na escolha de pseudoinversa com projeções dadas, unicidade de pseudoinversas mútuas com projeções dadas. O caso de projeções ortogonais = a pseudoinversa de Moore-Penrose: Propriedade de minimização de distância da imagem, expressão em termos da adjunta. Aplicação da pseudoinversa de Moore-Penrose à análise de dados: o método de regressão linear.
- Aula 20 – 16.11.21 (vídeo) – Pseudoinversas de transformações lineares. Definição e propriedades, projeções no domínio e no contradomínio associadas a uma pseudoinversa. O caso de transformações lineares bijetoras (unicidade da pseudoinversa nesse caso), sobrejetoras e injetoras. Ambiguidade na escolha de pseudoinversa com projeções dadas. Unicidade de pseudoinversas mútuas com projeções dadas. O caso de projeções ortogonais, a pseudoinversa de Moore-Penrose.
- Aula 19 – 12.11.21 (vídeo) – Consequências do Teorema do Núcleo e da Imagem, o posto e a nulidade de uma transformação linear: (a) caracterização de funcionais lineares (lema de Riesz) – enunciado; (b) caracterização de sobrejetividade e injetividade de transformações lineares pelo seu posto; (c) igualdade do posto de uma transformação linear e de sua adjunta (interlúdio: complementos ortogonais de subespaços vetoriais e suas projeções ortogonais). Consequências para matrizes – o posto de uma matriz, caracterização de matrizes invertíveis.
- Aula 18 – 9.11.21 (vídeo) – O Teorema do Núcleo e da Imagem: a imagem de um subconjunto do domínio e a imagem inversa de um subconjunto do contradomínio de uma função. O caso de transformações lineares: imagens e imagens inversas de subespaços vetoriais, o núcleo e a imagem de uma transformação linear. Caracterização de injetividade e de sobrejetividade de uma transformação linear, efeito sobre conjuntos l.i. e bases. O caso de domínios com dimensão finita: enunciado e prova do Teorema do Núcleo e da Imagem.
- Aula 17 – 5.11.21 (vídeo) – A matriz de uma transformação linear (iii): recapitulação – representação matricial de operações algébricas sobre transformações lineares (operações vetoriais, identificação de espaços vetoriais de transformações lineares com espaços vetoriais de matrizes, o produto de matrizes como representação matricial do produto ( = composição) de transformações lineares, a matriz transposta como representação matricial da adjunta, matriz zero e a matriz identidade, matriz inversa como matriz da inversa de uma transformação linear). O efeito de mudanças de base no domínio e no contradomínio de uma transformação linear sobre a sua matriz: matrizes de mudança de base, o caso de bases ortonormais (matrizes ortogonais).
- Aula 16 – 22.10.21 (vídeo) – A matriz de uma transformação linear (ii): recapitulação – representação matricial de operações algébricas sobre transformações lineares (operações vetoriais, identificação de espaços vetoriais de transformações lineares com espaços vetoriais de matrizes, o produto de matrizes como representação matricial do produto ( = composição) de transformações lineares). A matriz zero e a matriz identidade. A matriz inversa como matriz da inversa de uma transformação linear. Transposição de matrizes, a adjunta de uma transformação linear.
- Aula 15 – 19.10.21 (vídeo) – A matriz de uma transformação linear: recapitulação – determinação de uma transformação linear por seus valores numa base do domínio, a matriz de uma transformação linear num par de bases no domínio e no contradomínio, vetores-coluna. Exemplos simples. O caso de bases ortonormais. Representação matricial de operações algébricas sobre transformações lineares: operações vetoriais (pontuais), identificação de espaços vetoriais de transformações lineares com espaços vetoriais de matrizes, o produto de matrizes como representação matricial do produto ( = composição) de transformações lineares.
- Aula 14 – 18.10.21 (vídeo) – Transformações lineares (continuação): recapitulação – definição, notação e (contra)exemplos (zero, identidade, multiplicação por um escalar fixo, produto escalar com um vetor fixo), estrutura algébrica de espaços de transformações lineares (operações vetoriais pontuais, produto = composição e inversa). Um exemplo genérico de transformações lineares com domínio de dimensão finita. Imagem e imagem inversa de subconjuntos por uma transformação linear: núcleo e imagem, propriedade de subespaço vetorial, caracterização de injetividade de uma transformação linear pela trivialidade do seu núcleo. Determinação de uma transformação linear por seus valores numa base do domínio, a matriz de uma transformação linear num par de bases no domínio e no contradomínio, vetores-coluna.
- Aula 13 – 15.10.21 (vídeo) – Transformações lineares: definição, notação e (contra)exemplos (zero, identidade, multiplicação por um escalar fixo, translações por um vetor fixo, rotações em
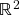 , traço e determinante de matrizes, derivada e integral, produto escalar com um vetor fixo). Estrutura algébrica de espaços de transformações lineares: operações vetoriais (pontuais), produto ( = composição) e inversa.
, traço e determinante de matrizes, derivada e integral, produto escalar com um vetor fixo). Estrutura algébrica de espaços de transformações lineares: operações vetoriais (pontuais), produto ( = composição) e inversa. - Aula 12 – 8.10.21 (vídeo) – O método de ortonormalização de Gram-Schmidt. Recapitulação: projeções ortogonais – definição e propriedades. Construção de bases ortogonais / ortonormais e conversão de bases em bases ortogonais / ortonormais usando projeções ortogonais. Comparação com o método geral de construção de bases finitas, exemplos simples.
- Aula 11 – 6.10.21 (vídeo) – Geometria do produto escalar (ii): recapitulação – desigualdade de Cauchy-Schwarz e suas consequências (lei dos cossenos, desigualdade triangular), propriedades da norma e da distância (desigualdade triangular, homogeneidade e não-degenerescência). Projeções ortogonais: o caso unidimensional – interpretação geométrica do produto escalar. Interpretação geométrica das componentes de um vetor numa base o.n.. Definição e propriedades da projeções ortogonal ao longo de um subespaço vetorial, minimização de distância a um vetor dado dentro de um subespaço vetorial.
- Aula 10 – 5.10.21 (vídeo) – Produtos escalares: recapitulação – definição e axiomas, ortogonalidade, conjuntos ortogonais e ortonormais, normalização de conjuntos ortogonais que não contém zero, bases ortogonais e ortonormais, componentes de um vetor em bases ortogonais e ortonormais. Geometria do produto escalar: comprimentos, distâncias e ângulos – norma (euclidiana), distância (euclidiana) e ângulo entre dois vetores. A desigualdade de Cauchy-Schwarz, sua prova e suas consequências (lei dos cossenos, desigualdade triangular). Relação de valores particulares do ângulo entre vetores com ortogonalidade e dependência linear. Propriedades da norma e da distância (desigualdade triangular, homogeneidade e não-degenerscência).
- Aula 9 – 1.10.21 (vídeo) – Produtos escalares: motivação (produto escalar canônico em
 ), definição e axiomas (simetria, positividade definida e bilinearidade). O produto escalar associado a uma base finita. Ortogonalidade, conjuntos ortogonais e ortonormais, normalização de conjuntos ortogonais que não contém zero. Bases ortogonais e ortonormais, normalização de uma base ortogonal, unicidade do produto escalar associado a uma base finita, componentes de um vetor em bases ortogonais e ortonormais.
), definição e axiomas (simetria, positividade definida e bilinearidade). O produto escalar associado a uma base finita. Ortogonalidade, conjuntos ortogonais e ortonormais, normalização de conjuntos ortogonais que não contém zero. Bases ortogonais e ortonormais, normalização de uma base ortogonal, unicidade do produto escalar associado a uma base finita, componentes de um vetor em bases ortogonais e ortonormais. - Aula 8 – 29.9.21 (vídeo) – Bases e dimensão de um espaço vetorial. Recapitulação: bases de um espaço vetorial. Número de vetores de uma base finita de um espaço vetorial = dimensão como propriedade intrínseca. Espaços vetoriais de dimensão finita e infinita: definição e exemplos (
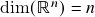 , espaços de funções de dimensão finita e infinita). Construção de bases de um subespaço vetorial de dimensão finita.
, espaços de funções de dimensão finita e infinita). Construção de bases de um subespaço vetorial de dimensão finita. - Aula 7 – 28.9.21 (vídeo) – Bases de um espaço vetorial. Recapitulação de (in)dependência linear. Bases: definição, componentes de um vetor ao longo de um elemento da base como “coordenadas lineares”, representação das operações vetoriais em termos das componentes de uma base, (contra)exemplos (base canônica de
 , espaços de funções). Bases finitas e dimensão de um espaço vetorial: resultados estruturais (1) e esboço de definição (número de elementos de uma base finita = número de “coordenadas lineares”)
, espaços de funções). Bases finitas e dimensão de um espaço vetorial: resultados estruturais (1) e esboço de definição (número de elementos de uma base finita = número de “coordenadas lineares”) - Aula 6 – 24.9.21 (vídeo) – Somatória vetorial: definição e propriedades (recapitulação). Combinações lineares, dependência linear e independência linear. Caracterização de independência linear de uma família finita de vetores como unicidade da representação de um vetor como combinação linear desses vetores. (In)dependência linear de subconjuntos: propriedades e exemplos.
- Aula 5 – 22.9.21 (vídeo) – Subespaços vetoriais: definição (recapitulação). Intersecção e soma de subespaços vetoriais. Por que a união de dois subespaços vetoriais não é em geral um subespaço vetorial. Exemplos e contraexemplos de subespaços vetoriais (2): soluções de sistemas lineares homogêneos e não-homogêneos, espaços de polinômios e de funções diferenciáveis. Somatória vetorial: definição e propriedades. Combinações lineares, dependência linear e independência linear.
- Aula 4 – 21.9.21 (vídeo) – Espaços vetoriais (reais): Exemplos (2): espaços de funções a valores num espaço vetorial, espaços de matrizes. Subespaços vetoriais: definição e estrutura de espaço vetorial herdado do espaço vetorial ambiente. Exemplos e contraexemplos de subespaços vetoriais (1). Intersecção e soma de subespaços vetoriais.
- Aula 3 – 17.9.21 (vídeo) – Espaços vetoriais (reais): definição e axiomas. Consequências simples dos axiomas, analogias e diferenças das operações vetoriais com a soma e o produto de escalares. Exemplos (1):
 , espaços de funções a valores reais.
, espaços de funções a valores reais. - Aula 2 – 15.9.21 (vídeo) – Operações vetoriais: origem geométrica (cont.). Espaços afins e função deslocamento: definição e propriedades. Definição da soma vetorial e derivação de suas propriedades (comutatividade, associatividade, elemento neutro e oposto). Escalares como fatores de escala para vetores de deslocamento e multiplicação escalar: o caso de escalares inteiros, propriedades (distributividade com respeito às somas escalar e vetorial, associatividade, elemento neutro). Escalares racionais: como definir multiplicação escalar? Interpretação geométrica. Espaços vetoriais (reais): definição e axiomas.
- Aula 1 – 14.9.21 (vídeo) – Informações sobre o funcionamento do curso. Motivação: o que são espaços vetoriais e qual a sua importância? Origem geométrica: vetores de deslocamento num espaço de pontos (espaço afim). Soma vetorial e seus axiomas. Multiplicação por escalares = fatores de escala (caso de escalares inteiros).
Bibliografia
Listamos aqui os textos que seguiremos mais de perto.
- Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969. Uma versão online gratuita dos dois volumes em inglês pode ser encontrada aqui).
- Notas de aula atualizadas periodicamente (última versão: 29.9.21).
(Observação: o link do livro disponibilizado acima parte de um servidor que, em princípio, oferece tais materiais legalmente. Se for comprovado que este não é o caso, os links serão retirados sem aviso prévio)
A lista abaixo indica textos suplementares que podem ser de utilidade para o aluno.
- Notas de aulas do Prof. Jerônimo C. Pellegrini (atualizadas periodicamente).
- Howard Anton, Chris Rorres, Álgebra Linear com Aplicações (décima edição). Bookman, 2012 (original em inglês: Linear Algebra with Applications – 9th Edition. Wiley, 2005).
- G. Strang, Introduction to Linear Algebra (5a. edição). Wellesley Cambridge Press, 2016.
Recomendações e material didático suplementar
É recomendado que o aluno tenha cursado anteriormente a disciplina BCN0404 – Geometria Analítica. Ocasionalmente, conceitos básicos da disciplina BCN0402 – Funções de Uma Variável – e.g. cálculo de integrais simples – podem ser empregados em exemplos.
Estrutura das atividades da disciplina
As aulas terão um formato híbrido – serão disponibilizadas assincronamente três aulas por semana (menos o número de dias de feriado na semana em questão coincidindo com os dias do horário presencial) de acordo com a carga didática da disciplina, sendo que duas delas serão também transmitidas sincronamente nas seguintes datas e horários (exceto feriados – estes serão repostos no período de reposição seguindo o calendário acadêmico de 2021):
- Terças-feiras, 19h00-21h00;
- Sextas-feiras, 19h00-21h00.
Reitero que a transmissão das aulas síncronas será gravada e disponibilizada posteriormente de maneira assíncrona. O link para a sala de reunião (Google Meet) onde cada aula será transmitida será divulgado por email e pelo Moodle com no máximo 30 minutos de antecedência por razões de segurança. A entrada nas salas de reunião só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de segurança e controle da participação dos alunos. Para realizar o vinculamento, recomendo seguir o tutorial do NTI para o procedimento.
As datas e horários acima foram escolhidas em função dos horários presenciais. O objetivo das aulas síncronas é permitir (dentro das limitações da internet de cada aluno e do docente) uma maior participação dos alunos.
Os links para o vídeo e a postagem de blog correspondentes a cada aula serão disponibilizados na lista de aulas.
Avaliação
A avaliação consistirá em dois tipos de atividades:
- Duas provas (P1, P2) a serem aplicadas na plataforma Moodle, no seguinte formato: haverá uma janela temporal de 72 horas para a prova ser feita. Uma vez iniciada dentro desse período, o aluno terá até 3 horas para enviar a resolução (período suficiente para lidar com eventuais dificuldades no envio) ou até que a janela temporal se encerre (o que ocorrer primeiro).
- Envio de resoluções de seleções de exercícios para cada uma das listas de exercícios
(ver a seção “Listas de exercícios” abaixo para mais detalhes). As
resoluções correspondentes a cada lista deverão também ser enviadas pelo
Moodle dentro de uma janela temporal de 72 horas.
Haverá uma prova de recuperação a ser agendada para o início do segundo quadrimestre letivo de 2021, no mesmo formato que a P1 e a P2 mas que cobrirá o conteúdo do curso inteiro.
Média preliminar: Mp = 0,25*(P1+P2) + 0,5*Ml , onde Ml é a média simples das resoluções das listas de exercícios.
Média final: Mf = 0,25*max(P1+P2 ,Rec+P1, Rec+P2) + 0,5*Ml
Critério de conversão de média preliminar (Mp) / final (Mf) para conceito preliminar (Cp) / final (Cf):
Cp (resp. Cf) = F – Mp (resp. Mf) < 4,5;
Cp (resp. Cf) = D – Mp (resp. Mf) = 4,5-5,2;
Cp (resp. Cf) = C – Mp (resp. Mf) = 5,3-6,9;
Cp (resp. Cf) = B – Mp (resp. Mf) = 7,0-8,4;
Cp (resp. Cf) = A – Mp (resp. Mf) = 8,5-10,0.
Sugestões de ferramentas gratuitas para digitalização de documentos em formato PDF usando a câmera de smartphones:
- Adobe Scan (Android, iOS);
- vFlat (somente para Android);
- Microsoft Office Lens (Android, iOS);
- Google Drive (ferramenta de digitalização integrada à nuvem da Google – aviso: esse recurso é mais limitado que o dos apps dedicados listados acima! Somente para Android).
Janelas das provas:
- P1 – 00h00 de terça-feira, 26.10 às 23h59 de quinta-feira, 28.10;
- P2 – 00h00 de segunda-feira, 13.12 às 23h59 de quarta-feira, 15.12;
- Sub – 00h00 de terça-feira, 21.12 às 23h59 de quinta-feira, 23.12 (acessível apenas a alunos que apresentarem justificativa formal por escrito para a ausência na P1 ou P2);
- Rec – a ser agendada no início do primeiro quadrimestre letivo de 2022.
Janelas de envio de resoluções das listas de exercícios:
- Listas 1 e 2 – 00h00 de terça-feira, 5.10 às 23h59 de quinta-feira, 7.10;
- Listas 3 e 4 – 00h00 de terça-feira, 19.10 às 23h59 de quinta-feira, 21.10;
- Listas 5 e 6 – 00h00 de quinta-feira, 25.11 às 23h59 de sábado, 27.11;
- Listas 7 e 8 – 00h00 de quarta-feira, 8.12 às 23h59 de sexta-feira, 10.12;
Durante cada janela de envio de resoluções de listas de exercícios, será aberta uma tarefa no Moodle com essa finalidade. Os detalhes sobre o envio das resoluções e as seleções de exercícios a serem resolvidos serão divulgados no início de cada janela.
Listas de exercícios
É extremamente importante que os alunos façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!
Monitoria, atendimento online e plantão de dúvidas
Haverá um plantão de dúvidas em videoconferência às quintas-feiras das 17h00 às 20h00, usando a plataforma Google Meet, tal como a transmissão síncrona das aulas
O plantão terá início em 16.9 – por razões de segurança, o link para a sala de reunião será divulgado por email e pelo Moodle no máximo 30 minutos antes do início de cada reunião.
Tal como na transmissão síncrona das aulas, a entrada nas salas de reunião dos plantões só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de controle da participação dos alunos.
Horários dos plantões de monitoria (início: 14.9), monitora – Alexssandra Thais Pereira Alves de Souza:
- 3as. feiras 13h-14h;
- 4as. feiras 17h-19h;
- 6as. feiras 12h-14h.
Por razões de segurança, o link para a sala de reunião do Google Meet onde o atendimento será feito deve ser acessado pelo Moodle.
Controle de frequência
A frequência será controlada mediante a participação nas aulas síncronas e nos plantões de dúvidas, bem como pela entrega das resoluções das seleções de exercícios das listas. A contabilização de presença nas transmissões síncronas das aulas será semanal – basta que o aluno compareça a uma aula síncrona da semana para que sua presença nas aulas daquela semana seja computada. Observo que, em virtude do caráter remoto das aulas, o controle de frequência não será usado para fins de reprovação por falta.
Roteiro
Seguiremos de maneira aproximada o cronograma sugerido para o curso de AlgLin pelo Gradmat, com algumas modificações na ordem e na ênfase – para uma descrição mais detalhada dos tópicos de cada aula, confira a lista das aulas. Uma descrição sucinta dos tópicos do curso na ordem a ser seguida pode ser vista abaixo.
- Espaços vetoriais: motivação, definição e exemplos (Anton-Rorres: seção 5.1; Apostol: seções 1.1 a 1.5; notas do Pellegrini: seção 1.4).
- Subespaços vetoriais: definição e exemplos (Anton-Rorres: seção 5.2; Apostol: seção 1.6; notas do Pellegrini: seção 1.5).
- Combinações lineares, dependência linear e independência linear. Subespaços vetoriais gerados por um conjunto de vetores (Anton-Rorres: seções 5.2 e 5.3; Apostol: seções 1.6 e 1.7; notas do Pellegrini: seção 2.1).
- Bases
e dimensão de um (sub)espaço vetorial, componentes de um vetor numa
base. Mudança de base (Anton-Rorres: seção 5.4; Apostol: seções 1.8 a
1.10; notas do Pellegrini: seções 2.2 e 2.4).
- Produtos escalares: definição e propriedades. Geometria do produto escalar: a desigualdade de Cauchy-Schwarz.
- Projeções ortogonais, bases ortogonais e ortonormais. Ortonormalização de Gram-Schmidt.
- Transformações lineares: definição e exemplos. A adjunta de uma transformação linear com respeito a um produto escalar.
- A
matriz de uma transformação linear numa base. O efeito da mudança de
base na matriz de uma transformação linear, matrizes de mudança de base.
- Núcleo e imagem de uma transformação linear. Posto e nulidade.
- Sistemas lineares, transformações lineares e matrizes. Operações elementares e escalonamento de matrizes: algoritmos de eliminação Gaussiana e de Gauss-Jordan.
- O determinante de uma transformação linear e de uma matriz.
- Autovalores e autovetores: definição e interpretação geométrica. O polinômio característico.
- Bases de autovetores e diagonalização de transformações lineares.
- Tópicos suplementares (a serem administrados ao longo do curso se houver tempo): a pseudoinversa de uma transformação linear e decomposição em valores singulares, aplicações (regressão linear, análise de componentes principais).

