Plano de ensino – AlgLin – 3q’24 – Pedro Lauridsen Ribeiro

Author: Jun Lu; License: Creative Commons Attribution 4.0 International

Esta é a página sobre a disciplina MCTB001 – Álgebra Linear, ministrada no terceiro quadrimestre de 2024 para a turma A Noturno – campus Santo André, nos seguintes horários:

2as. feiras 19h00-21h00, sala A-S311-1;
4as. feiras 21h00-23h00, sala A-S311-2;
5as. feiras 19h00-21h00, sala A-S113-0.

Aqui encontram-se informações específicas sobre a turma acima.

Novidades

Notícias recentes sobre o funcionamento do curso serão disponibilizadas aqui.

(25.10.24) As notas de aula e a versão NEE destas foram atualizadas.
(2.10.24) A versão NEE das notas de aula está disponível.
(2.10.24) As notas de aula foram atualizadas.

Aulas

Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.

Aula 28 – 16.12.24 – Sistemas lineares (iv): exemplos de aplicação – 1.) sistema linear com uma única solução; 2.) sistema linear sem solução; 3.) sistema linear com mais de uma solução (obtenção da solução geral). Determinantes: funções determinantes – definição, propriedades, determinação por seu valor numa base ordenada, a função determinante associada a uma base ordenada. O determinante de uma transformação linear: definição, independência da escolha de base ordenada e propriedades, cálculo por eliminação gaussiana. Autovalores e autovetores de uma transformação linear (esboço): equação de autovalor, autoespaço de uma transformação linear associada a um autovalor, o polinômio característico de uma transformação linear (raízes = autovalores), cálculo por eliminação gaussiana. Diagonalização ( = obtenção de uma base de autovetores) de uma transformação linear (preâmbulos da Lista 7 e da Lista 8).
Aula 27 – 12.12.24 – Sistemas lineares (iii): recapitulação – forma matricial e forma expandida de sistemas lineares. A matriz aumentada de um sistema linear na forma matricial. Descrição e efeito do algoritmo de eliminação gaussiana ( = escalonamento de matrizes), forma (matricial) escalonada de um sistema linear, pivôs de uma matriz escalonada (em linhas = “row echelon form”). Expressão dos critérios de existência e unicidade de soluções na forma escalonada, o efeito da eliminação gaussiana sobre o sistema linear homogêneo associado. Prescrição de valores para as variáveis fora dos pivôs de modo a obter a solução particular e uma base de soluções l.i. do sistema linear homogêneo associado no caso de solução não-única (preâmbulo da Lista 7).
Aula 26 – 11.12.24 – Sistemas lineares (ii): recapitulação – generalidades (definição, sistemas lineares homogêneos e não-homogêneos, o sistema linear homogêneo associado a um sistema linear geral, critérios de existência e unicidade de soluções, a solução geral de um sistema linear, princípio de superposição para sistemas lineares homogêneos). Forma matricial de sistemas lineares. Interlúdio: núcleo e imagem da adjunta de uma transformação linear, igualdade do posto de uma matriz e o de sua transposta. O algoritmo de eliminação gaussiana = escalonamento de matrizes (i): preliminares – ação de transformações lineares invertíveis sobre (os dois lados de) um sistema linear, operações elementares numa base do contradomínio de uma transformação linear e seu efeito sobre a matriz desta (exercícios 13 e 16 da Lista 5, preâmbulo da Lista 7).
Aula 25 – 9.12.24 – O Teorema do Núcleo e da Imagem (iv): recapitulação – núcleo e imagem de projeções lineares, invertibilidade parcial de uma transformação linear. Pseudoinversas: motivação, projeções fonte e alvo, o caso particular de transformações lineares sobrejetora, injetoras e bijetoras, critério de unicidade. O caso de projeções fonte e alvo ortogonais, pseudoinversa de Moore-Penrose, aplicações – regressão linear, método dos mínimos quadrados para melhor ajuste de modelos lineares. Sistemas lineares (i): generalidades – definição, sistemas lineares homogêneos e não-homogêneos, o sistema linear homogêneo associado a um sistema linear geral. Critérios de existência e unicidade de soluções, a solução geral de um sistema linear, princípio de superposição para sistemas lineares homogêneos (exercícios 14, 15 e 16 da Lista 5, preâmbulo da Lista 7).
Aula 24 – 5.12.24 – O Teorema do Núcleo e da Imagem (iii): recapitulação – imagem e imagem inversa de um subconjunto por uma transformação linear, o caso particular da imagem inversa de um subconjunto unitário ( = conjunto de soluções de um sistema linear), imagem e imagem inversa de subespaços vetoriais por uma transformação linear, o núcleo de uma transformação linear, aracterização de sobrejetividade e injetividade de transformações lineares, posto e nulidade de uma transformação linear, o Teorema do Núcleo e da Imagem. Consequências da prova do Teorema do Núcleo e da Imagem (i): posto de matrizes, núcleo e imagem de projeções lineares, invertibilidade parcial de uma transformação linear (páginas 51 a 54 das notas de aula, páginas 89 a 94 da versão NEE, exercício 14 da Lista 5).
Aula 23 – 4.12.24 – O Teorema do Núcleo e da Imagem (ii): recapitulação – imagem e imagem inversa de um subconjunto por uma transformação linear, o caso particular da imagem inversa de um subconjunto unitário ( = conjunto de soluções de um sistema linear). Imagem e imagem inversa de subespaços vetoriais por uma transformação linear, o núcleo de uma transformação linear. Caracterização de sobrejetividade e injetividade de transformações lineares. Posto e nulidade de uma transformação linear, o Teorema do Núcleo e da Imagem (enunciado, prova e consequências) (páginas 51 a 54 das notas de aula, páginas 89 a 94 da versão NEE).
Aula 22 – 2.12.24 – Transformações lineares (v): recapitulação – determinação de uma transformação linear por seus valores numa base, a matriz de uma transformação linear num par de bases ordenadas no domínio e no contradomínio, expressão matricial das operações algébricas sobre transformações lineares (operações vetoriais, produto, inversão e adjunta). Interlúdio: transformações lineares implementando mudanças de bases ordenadas, matrizes de mudança de base. O caso de bases ordenadas ortonormais: transformações lineares ortogonais. O efeito de mudanças de base sobre a matriz de uma transformação linear. O Teorema do Núcleo e da Imagem (i): preliminares – imagem e imagem inversa de um subconjunto por uma transformação linear (páginas 50 a 52 das notas de aula, páginas 87 a 90 da versão NEE).
Aula 21 – 25.11.24 – Transformações lineares (v): recapitulação – determinação de uma transformação linear por seus valores numa base, a matriz de uma transformação linear num par de bases ordenadas no domínio e no contradomínio, expressão matricial das operações algébricas sobre transformações lineares (operações vetoriais, produto e inversão). Expressão matricial das operações algébricas sobre transformações lineares (ii): transposição de matrizes, a adjunta de uma transformação linear (com respeito a um par de produtos escalares no domínio e no contradomínio). Propriedades da adjunta: interação com as demais operações algébricas sobre transformações lineares, involutividade (páginas 45 a 49 das notas de aula, páginas 78 a 87 da versão NEE).
Aula 20 – 21.11.24 – Transformações lineares (iv): recapitulação – determinação de uma transformação linear por seus valores numa base, expressão das componentes do valor de uma transformação linear num vetor numa base do contradomínio em termos das componentes desse vetor numa base do domínio (em dimensão finita). Interlúdio: bases ordenadas, o vetor-coluna de um vetor numa base ordenada. A matriz de uma transformação linear num par de bases ordenadas no domínio e no contradomínio. Expressão matricial das operações algébricas sobre transformações lineares (i): operações vetoriais, produto e inversão (páginas 45 a 49 das notas de aula, páginas 78 a 87 da versão NEE).
Aula 19 – 18.11.24 – Transformações lineares (iii): recapitulação – operações algébricas sobre transformações lineares (operações vetoriais, produto – composição, inversão), problemas com comutatividade do produto. A matriz de uma transformação linear (i): preliminares – determinação de uma transformação linear por seus valores numa base, expressão das componentes do valor de uma transformação linear num vetor numa base do contradomínio em termos das componentes desse vetor numa base do domínio (em dimensão finita). O caso particular de funcionais lineares: expressão unívoca em termos do produto escalar com um vetor (lema de Riesz). Interlúdio: bases ordenadas, o vetor-coluna de um vetor numa base ordenada. A matriz de uma transformação linear num par de bases ordenadas no domínio e no contradomínio (páginas 43 a 46 das notas de aula, páginas 75 a 81 da versão NEE).
Aula 18 – 14.11.24 – Transformações lineares (ii): recapitulação – definição, axiomas de transformações lineares, convenções e nomenclatura (funcionais lineares, espaços de transformações lineares, espaços duais). Estrutura de espaço vetorial em espaços de transformações lineares (ii): soma e múltiplos escalares de transformações lienares são também transformações lineares. Operações algébricas adicionais em espaços de transformações lineares (i): produto ( = composição) de transformações lineares é também uma transformação linear, propriedades (distributividade, associatividade e elemento neutro), problemas com comutatividade. A inversa de uma transformação linear também é uma transformação linear (páginas 41 a 44 das notas de aula, páginas 71 a 78 da versão NEE).
Aula 17 – 11.11.24 – Transformações lineares (i): definição, axiomas de transformações lineares e suas consequências. Convenções e nomenclatura: funcionais lineares, espaços de transformações lineares, espaços duais. Exemplos e contraexemplos de transformações lineares: 1.) zero; 2.) múltiplos escalares; 3.) projeções ortogonais ao longo de um subespaço vetorial; 4.) funcional linear dado pelo produto escalar com um vetor fixo; 5.) determinação de uma transformação linear por seus valores numa base ortonormal (finita); 6.) expressão de uma transformação linear em termos de um produto escalar no domínio e uma base (finita) no contradomínio; 7.) derivadas; 8.) um contraexemplo em 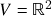$V=\mathbb{R}^2$ ; 9.) representação de um vetor numa base finita. Estrutura de espaço vetorial em espaços de transformações lineares (i): a soma de duas transformações lineares é uma transformação linear (páginas 41 a 43 das notas de aula, páginas 71 a 76 da versão NEE).
Aula 16 – 7.11.24 – Produtos escalares (vi): recapitulação – algoritmo de ortonormalização de Gram-Schmidt (resumo e propriedades), o papel das projeções ortogonais. O complemento ortogonal de um subespaço vetorial de dimensão finita e a projeção ortogonal associada. Exemplo de aplicação do algoritmo de Gram-Schmidt (construção de uma base ortonormal adaptada a um subespaço vetorial) (páginas 38 e 39 das notas de aula, páginas 67 a 70 da versão NEE).
Aula 15 – 4.11.24 – Produtos escalares (iv): ortogonalizacão e ortonormalização de bases – o algoritmo de Gram-Schmidt. Descrição do algoritmo, o papel das projeções ortogonais (páginas 38 e 39 das notas de aula, páginas 67 a 70 da versão NEE).
Aula 14 – 31.10.24 – Produtos escalares (iii): geometria do produto escalar (ii) – recapitulação (norma e distância (euclideanas) associadas a um produto escalar, desigualdade de Cauchy-Schwarz), ângulo entre vetores não-nulos (lei dos cossenos), teorema de Pitágoras. Consequências da desigualdade de Cauchy-Schwarz: desigualdade triangular para a norma e a distância. Axiomas de norma e de distância. Consistência geométrica da noção de ângulo entre vetores (ortogonalidade, colinearidade). Projeções ortogonais ao longo de um subespaço vetorial: definição em termos de uma base ortonormal do subespaço vetorial, propriedades, independência da escolha de base, minimização de distância (páginas 33 a 38 das notas de aula, páginas 59 a 67 da versão NEE).
Aula 13 – 30.10.24 – Produtos escalares (ii): recapitulação – definição abstrata de produto escalar ( = produto interno) num espaço vetorial, consequências dos axiomas de produto escalar (bilinearidade, produto escalar com o vetor zero é zero, comportamento com respeito a combinações lineares). Subconjuntos ortogonais e ortonormais, independência linear de subconjuntos ortogonais não-vazios que não contém o zero, unicidade do produto escalar associado a uma base em termos da ortonormalidade dessa base. Geometria do produto escalar (i): norma e distância (euclideanas) associadas a um produto escalar, ângulo entre vetores e desigualdade de Cauchy-Schwartz – enunciado e prova (páginas 31 a 34 das notas de aula, páginas 56 a 61 da versão NEE).
Aula 12 – 24.10.24 – Produtos escalares (i): motivação – o produto escalar canônico em $\mathbb{R}^n$ , axiomas de produto escalar. Definição abstrata de produto escalar ( = produto interno) num espaço vetorial. Consequências dos axiomas de produto escalar – bilinearidade. Exemplos de produtos escalares (i): o produto escalar associado a uma base finita. Ortogonalidade e ortonormalidade, subconjuntos ortogonais e ortonormais, independência linear de subconjuntos ortogonais não-vazios que não contém o zero (páginas 31 e 32 das notas de aula, páginas 55 a 58 da versão NEE).
Aula 11 – 23.10.24 – Combinações lineares e (in)dependência linear (v): recapitulação – Bases de um espaço vetorial, componentes de um vetor numa base, o caso de bases finitas – resultados fundamentais (i) 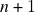$n+1$ vetores no subespaço vetorial gerado por $n$ vetores linearmente independentes são linearmente dependentes, (ii) acrescentar a um conjunto lineamente independente um vetor que não pertence ao subespaço vetorial gerado pelo conjunto mantém independência linear. Consequências de (i) e (ii): (iii) se um espaço vetorial admite uma base finita, então todas as suas bases tem o mesmo número de vetores, (iv) se um subconjunto linearmente independente desse mesmo espaço vetorial tem o mesmo número de vetores que uma base, então ele mesmo é uma base (critério dimensional para bases). Dimensão de um espaço vetorial = número de vetores numa base finita. Algoritmo de construção de bases de um espaço vetorial de dimensão finita, bases adaptadas a um subespaço vetorial, exemplo de aplicação do algoritmo (páginas 24 a 29 das notas de aula, páginas 45 a 53 da versão NEE).
Aula 10 – 21.10.24 – Combinações lineares e (in)dependência linear (iv): recapitulação – Bases de um espaço vetorial, componentes de um vetor numa base ( = sistema de “coordenadas lineares”), espaços vetoriais de dimensão finita e infinita, dimensão de um espaço vetorial = número de vetores numa base finita. Identificação de um espaço vetorial com o subespaço vetorial das funções de uma base em $\mathbb{R}$ que se anulam fora de um subconjunto finito, representação de um vetor numa base. O caso de bases finitas: identificação com $\mathbb{R}^n$ por meio da representação numa base. 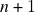Dimensão de um espaço vetorial ( = número de vetores numa base finita) e construção de bases finitas: resultados fundamentais (i) – $n+1$ vetores no subespaço vetorial gerado por $n$ vetores linearmente independentes são linearmente dependentes, acrescentar a um conjunto lineamente independente um vetor que não pertence ao subespaço vetorial gerado pelo conjunto mantém independência linear (páginas 24 a 27 das notas de aula, páginas 45 a 50 da versão NEE).
Aula 9 – 17.10.24 – Combinações lineares e (in)dependência linear (iii): recapitulação – o subespaço (vetorial) gerado por = varredura (span) linear de um subconjunto de um espaço vetorial. Ação das operações vetoriais sobre os coeficientes de combinações lineares. O caso de subconjuntos linearmente independentes: unicidade da representação de um vetor no subespaço gerado. Bases de um espaço vetorial, componentes de um vetor numa base ( = sistema de “coordenadas lineares”). Exemplos e contraexemplos de bases: a base canônica de $\mathbb{R}^n$ e de espaços de funções de um domínio finito a valores reais, o caso de domínios infinitos, monômios como base do espaço dos polinômios. Espaços vetoriais de dimensão finita e infinita, dimensão de um espaço vetorial = número de vetores numa base finita (páginas 23 a 25, 27 e 28 das notas de aula, páginas 42 a 47, 50 e 51 da versão NEE).
Aula 8 – 16.10.24 – Combinações lineares e (in)dependência linear (ii): recapitulação – combinações lineares triviais e não-triviais. (In)dependência linear de listas finitas de vetores: definição, interpretação como (falta de) ambiguidade na escolha de “coordenadas lineares” e (im)possibilidade de expressar um vetor da lista como combinação linear dos demais. Subconjuntos linearmente dependentes e linearmente independentes: definição, propriedades e exemplos, o caso de subconjuntos finitos. O subespaço (vetorial) gerado por um subconjunto de um espaço vetorial (páginas 19 a 23 das notas de aula, páginas 36 a 43 da versão NEE).
Aula 7 – 14.10.24 – Subespaços vetoriais (iii): recapitulação – definição e estrutura de espaço vetorial herdada do espaço vetorial ambiente. Contra)exemplos de subespaços vetoriais (ii): espaços de polinômios, espaços de funções deriváveis. Interlúdio: somatória vetorial – definição recursiva e propriedades. Combinações lineares e (in)dependência linear (i): definição, combinações lineares triviais e não-triviais. (In)dependência linear de listas finitas de vetores: definição e interpretação como (falta de) ambiguidade na escolha de “coordenadas lineares” (páginas 14, 15 e 17 a 19 das notas de aula, páginas 27, 28 e 33 a 36 da versão NEE).
Aula 6 – 10.10.24 – Subespaços vetoriais (ii): recapitulação – definição e estrutura de espaço vetorial herdada do espaço vetorial ambiente, prova da validade dos axiomas de espaço vetorial num subespaço vetorial. (Contra)exemplos de subespaços vetoriais (i): subespaço trivial, interseções e somas de subespaços vetoriais, quando uniões de subespaços vetoriais falham em ser subespaços vetoriais, conjuntos de soluções de sistemas lineares (páginas 14 a 17 das notas de aula, páginas 27 a 33 da versão NEE).
Aula 5 – 9.10.24 – Espaços vetoriais (reais) (iii): recapitulação – axiomas de espaço vetorial. Exemplos de espaços vetoriais (i): 1.) 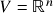$V=\mathbb{R}^n$ (em particular, 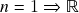$n=1\Rightarrow\mathbb{R}$ como espaço vetorial); 2.) espaços de funções a valores reais, $\mathbb{R}^n$ como caso particular; 3.) espaços de funções a valores num espaço vetorial. 4.) espaços de matrizes reais com $m$ linhas e $n$ colunas, identificação com $\mathbb{R}^{mn}$ . 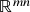Subespaços vetoriais (i): definição e estrutura de espaço vetorial herdada do espaço vetorial ambiente (páginas 11 a 15 das notas de aula, páginas 22 a 28 da versão NEE).
Aula 4 – 7.10.24 – Espaços vetoriais (reais) (ii): definição e axiomas. Consequências simples dos axiomas, analogias e diferenças das operações vetoriais com a soma e o produto de escalares (páginas 8 a 11 das notas de aula, páginas 15 a 22 da versão NEE).
Aula 3 – 3.10.24 – Origem geométrica das operações vetoriais (iii): recapitulação – soma vetorial e suas propriedades (comutatividade, associatividade, elemento neutro e oposto), escalares como fatores de escala para vetores de deslocamento e multiplicação escalar: escalares naturais, inteiros e racionais – propriedades (distributividade com respeito às somas escalar e vetorial, associatividade, elemento neutro) e interpretação geométrica. O caso de escalares reais, o conceito de espaço vetorial. Espaços vetoriais (reais) (i): definição e axiomas (páginas 2 a 9 das notas de aula, páginas 3 a 18 da versão NEE).
Aula 2 – 2.10.24 – Origem geométrica das operações vetoriais (ii): recapitulação – espaços afins e função deslocamento: definição e propriedades. Definição da soma vetorial e derivação de suas propriedades (comutatividade, associatividade, elemento neutro e oposto). Escalares como fatores de escala para vetores de deslocamento e multiplicação escalar: o caso de escalares naturais, propriedades (distributividade com respeito às somas escalar e vetorial, associatividade, elemento neutro) (páginas 1 a 5 das notas de aula, páginas 1 a 10 da versão NEE).
Aula 1 – 30.9.24 – Informações sobre o funcionamento do curso. Motivação: o que são espaços vetoriais e qual a sua importância? Origem geométrica das operações vetoriais (i): vetores de deslocamento num espaço de pontos (espaço afim), definição da soma vetorial, enunciado dos axiomas da soma vetorial (comutatividade, associatividade, existência de elemento neutro e existência de oposto) (páginas 1 a 3 das notas de aula, páginas 1 a 5 da versão NEE).

Bibliografia

Listamos aqui os textos que seguiremos mais de perto.

Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969).
Notas de aula serão disponibilizadas aqui à medida que o conteúdo for apresentado.

A lista abaixo indica textos suplementares que podem ser de utilidade para o aluno.

Notas de aulas do Prof. Jerônimo C. Pellegrini (atualizadas periodicamente).
Howard Anton, Chris Rorres, Álgebra Linear com Aplicações (décima edição). Bookman, 2012 (original em inglês: Linear Algebra with Applications – 9th Edition. Wiley, 2005).
G. Strang, Introduction to Linear Algebra (5a. edição). Wellesley Cambridge Press, 2016.

Recomendações e material didático suplementar

É recomendado que o aluno tenha cursado anteriormente a disciplina BCN0404 – Geometria Analítica. Ocasionalmente, conceitos básicos da disciplina BCN0402 – Funções de Uma Variável – e.g. cálculo de integrais simples – podem ser empregados em exemplos.

Material suplementar – cursos online, vídeos:

MIT OpenCourseWare – 18.06SC Linear Algebra (Fall 2011) – Prof. Gilbert Strang
MIT OpenCourseWare – 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning (Spring 2018) – Prof. Gilbert Strang
MIT OpenCourseWare – RES.18-010 A 2020 Vision of Linear Algebra (Spring 2020) – Prof. Gilbert Strang
YouTube – Canal 3Blue1Brown – The essence of linear algebra – Introdução e playlist das aulas (16 vídeos)

Os cursos do Prof. Gilbert Strang no MIT são famosos pela abordagem inovadora, motivada por aplicações modernas da Álgebra Linear (representação e análise de dados, aprendizado de máquina, etc.) e que pode ser vista como complementar ao ponto de vista adotado neste curso, embora com vários pontos em comum. A série de vídeos The essence of linear algebra, por sua vez, busca trazer uma compreensão visual intuitiva dos conceitos básicos do assunto.

Avaliação

Média preliminar:
M_p = 0,3*(P₁+P₂) + 0,4*M_t, onde M_t é a média dos testes online no Moodle (valendo de 0 a 10).
Média final:
M_p = 0,3*max(P₁+P₂, Rec+P₁, Rec+P₂) + 0,4*M_t
Critério de conversão de média preliminar (M_p) / final (M_f) para conceito preliminar (C_p) / final (C_f): C_p (resp. C_f) = F – M_p (resp. M_f) < 4,5;
C_p (resp. C_f) = D – M_p (resp. M_f) = 4,5-5,2;
C_p (resp. C_f) = C – M_p (resp. M_f) = 5,3-6,9;
C_p (resp. C_f) = B – M_p (resp. M_f) = 7,0-8,4;
C_p (resp. Cf) = A – M_p (resp. M_f) = 8,5-10,0.
A prova substitutiva só poderá ser feita por participantes que não puderem comparecer a uma das provas, com justificativa formal por escrito da ausência entregue ao docente no máximo até o horário de início da prova substitutiva. Preferencialmente o documento físico original deve ser entregue; se não por possível (e.g. pelo mesmo ser exigido para justificar ausência em provas de outras disciplinas), será aceita uma cópia digitalizada enviada por email mas será exigido nesse caso que @ participante apresente o documento original para conferência dentro do mesmo prazo.
A prova de recuperação será aplicada no início do 1q’25, no mesmo formato que a P₁ e a P₂ mas que cobrirá o conteúdo do curso inteiro. Apenas participantes que ficaram com conceitos preliminares D e F (ver critério acima) após a aplicação da prova substitutiva poderão fazer essa prova.
Datas das provas:

P1 – 11.11 (segunda-feira);
P2 – 18.12 (quarta-feira);
Sub – 19.12 (quinta-feira, se houver necessidade);
Rec – início do primeiro quadrimestre de 2025, a divulgar.

Listas de exercícios

É extremamente importante que @s participantes façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!

@s participantes que assim desejarem poderão entregar as suas resoluções das listas correspondentes à matéria de cada prova nas seguintes datas:

P1 – 13.11;
P2 – data da Rec.

Tais listas serão avaliadas nos casos de média final limítrofe para aprovação (ver tabela de conversão de conceitos acima), convertendo-se num bônus de até 1,5 ponto na média final.

Testes online (Moodle)

Haverá quatro (4) testes online na plataforma Moodle. @s participantes deverão receber as informações detalhadas sobre cada teste diretamente nos seus emails institucionais ((at)aluno.ufabc.edu.br), e deverão logar-se na plataforma com seu login e senha institucionais para fazer os testes.

Os exercícios cobertos nos testes online constituem uma seleção mínima de exercícios e não substituem no estudo individual a resolução das listas de exercícios acima, que são mais abrangentes e completas.

Cronograma de janelas de resolução dos testes:

Teste 1 – 22.10 a 25.10;
Teste 2 – 7.11 a 10.11;
Teste 3 – 5.12 a 8.12;
Teste 4 – 14.12 a 17.12.

Monitoria, atendimento online e plantão de dúvidas

A partir de terça-feira, 1.10 haverá monitoria presencial nas seguintes datas e horários:

Clayton Bomfim Biscalchini – 3as. feiras, 17h30-19h00 e 4as. feiras, 12h00-13h30, sala A-S304-1 (campus SA).

O monitor também fará atendimento online assíncrono num grupo de Telegram e num fórum do Moodle ainda a ser criado (mais informações a respeito em breve).

Haverá também plantões de dúvidas por videoconferência (Google Meet) a partir (excepcionalmente) de sexta-feira, 4.10 que terão lugar a partir de 8.10 às terças-feiras, sempre das 18h00 às 21h00. Observar que, por motivos de segurança e privacidade, essas informações só serão divulgadas no máximo 30 minutos antes do início do plantão. Para acessar a sala de reunião será necessário usar a conta Google vinculada ao endereço de email institucional da UFABC ((at)aluno.ufabc.edu.br). Veja o tutorial do NTI https://www.youtube.com/watch?v=Rf4kIbb4_sk para fazer a vinculação caso isso já não tenha sido feito. Reitero que o acesso à sala será tacitamente negado a contas Google que não satisfaçam a essa condição, por razões de segurança. O link da sala será divulgado por email pouco (no máximo 30 minutos) antes do início de cada plantão.

Finalmente, o Moodle terá um fórum aberto de perguntas e respostas onde @s participantes poderão tirar suas dúvidas assincronamente com o docente e/ou colegas.

Roteiro

Seguiremos de maneira aproximada o cronograma sugerido para o curso de AlgLin pelo Gradmat, com algumas modificações na ordem e na ênfase – para uma descrição mais detalhada dos tópicos de cada aula, confira a lista das aulas. Uma descrição sucinta dos tópicos do curso na ordem a ser seguida pode ser vista abaixo.

Espaços vetoriais: motivação, definição e exemplos (Anton-Rorres: seção 5.1; Apostol: seções 1.1 a 1.5; notas do Pellegrini: seção 1.4).
Subespaços vetoriais: definição e exemplos (Anton-Rorres: seção 5.2; Apostol: seção 1.6; notas do Pellegrini: seção 1.5).
Combinações lineares, dependência linear e independência linear. Subespaços vetoriais gerados por um conjunto de vetores (Anton-Rorres: seções 5.2 e 5.3; Apostol: seções 1.6 e 1.7; notas do Pellegrini: seção 2.1).
Bases e dimensão de um (sub)espaço vetorial, componentes de um vetor numa base. Mudança de base (Anton-Rorres: seção 5.4; Apostol: seções 1.8 a 1.10; notas do Pellegrini: seções 2.2 e 2.4).
Produtos escalares: definição e propriedades. Geometria do produto escalar: a desigualdade de Cauchy-Schwarz.
Projeções ortogonais, bases ortogonais e ortonormais. Ortonormalização de Gram-Schmidt.
Transformações lineares: definição e exemplos. A adjunta de uma transformação linear com respeito a um produto escalar.
A matriz de uma transformação linear numa base. O efeito da mudança de base na matriz de uma transformação linear, matrizes de mudança de base.
Núcleo e imagem de uma transformação linear. Posto e nulidade.
Sistemas lineares, transformações lineares e matrizes. Operações elementares e escalonamento de matrizes: algoritmos de eliminação Gaussiana e de Gauss-Jordan.
O determinante de uma transformação linear e de uma matriz.
Autovalores e autovetores: definição e interpretação geométrica. O polinômio característico.
Bases de autovetores e diagonalização de transformações lineares.
Tópicos suplementares (a serem administrados ao longo do curso se houver tempo): a pseudoinversa de uma transformação linear e decomposição em valores singulares, aplicações (regressão linear, análise de componentes principais).