Plano de ensino – CVT – QS5 – 1q’22

Este é o plano de ensino para a disciplina MCTB010 – Cálculo Vetorial e Tensorial (CVT) conforme ministrada no primeiro quadrimestre letivo de 2022 = quinto Quadrimestre Suplementar (QS) no formato de Estudo Dirigido.

Aqui encontram-se informações específicas para o Estudo Dirigido.

Novidades

Notícias recentes sobre o funcionamento do curso serão postadas aqui.

Aulas

Os links para o material de cada aula (vídeo e/ou blog), acompanhados de uma breve descrição desta, estão listados abaixo.

Aula 21 – 12.5.22 (vídeo) – Álgebra Exterior (xii): operador * de Hodge (ii) – recapitulação (definição, linearidade, ação sobre $p$ -formas na base induzida pela base ordenada ortonormal que determina *, inversa, fórmula de Laplace para o determinante de uma transformação linear). Aplicações (ii): fórmula de Laplace para a inversa de uma matriz não-singular. Dependência de * com respeito à orientação relativa da base ordenada ortonormal que o determina. 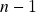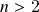O produto vetorial de $n-1$ vetores num espaço vetorial $n$ -dimensional ( $n>2$ ): definição, propriedades (( 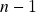$n-1$ )-linearidade, anti-simetria, ortogonalidade e norma), cálculo de componentes, interpretação geométrica. O produto misto, relação com determinantes e volumes de paralelepípedos $n$ -dimensionais. Produto escalar de produtos vetoriais como consequência da fórmula de Cauchy-Binet. 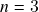O produto vetorial duplo à esquerda e à direita de três vetores: definição, redução à aplicação sucessiva de dois produtos vetoriais no caso $n=3$ , relação com o produto escalar. Não-associatividade do produto vetorial para 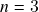$n=3$ . Identidades vetoriais.
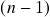Aula 20 – 11.5.22 (vídeo) – Álgebra Exterior (xi): operador * de Hodge (i) – definição, linearidade, ação sobre $p$ -formas na base induzida pela base ordenada ortonormal que determina *, inversa. Exemplos de cálculo – 1-formas e $(n-1)$ -formas. Aplicações (i): fórmula de Laplace para o determinante de uma transformação linear.
Aula 19 – 5.5.22 (vídeo) – Álgebra Exterior (x): recapitulação – produto exterior (definição = alternação do produto tensorial, propriedades = bilinearidade, comutatividade graduada e associatividade, eliminando o fator combinatório no produto exterior, 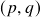$(p,q)$ -embaralhamentos). Produto exterior com mais de dois fatores. O caso do produto exterior de $p$ 1-formas: identidade de Cauchy-Binet, identidade de Lagrange como caso particular.
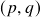Aula 18 – 4.5.22 (vídeo) – Álgebra Exterior (ix): recapitulação – produto exterior (definição = alternação do produto tensorial, bilinearidade, o efeito da alternação sobre $p$ -formas). O papel do fator combinatório e prova da associatividade do produto exterior. Comutatividade graduada. Eliminando o fator combinatório no produto exterior, $(p,q)$ -embaralhamentos. Produto exterior com mais de dois fatores.
Aula 17 – 28.4.22 (vídeo) – Álgebra Exterior (viii): produto exterior – definição (alternação do produto tensorial), preservação de multilinearidade e anti-simetria, bilinearidade. O efeito da alternação sobre $p$ -formas, o papel do fator combinatório sobre a associatividade do produto exterior (i).
Aula 16 – 27.4.22 (vídeo) – Álgebra Exterior (vii): recapitulação – $p$ -vetores (definição, base de $p$ -vetores associada a uma base ordenada ortonormal, $p$ -formas como funcionais lineares no espaço de $p$ -vetores). Os produtos escalares associados à base de formas de volume e à base de $p$ -vetores gerados por uma base ordenada ortonormal. O produto exterior: definição.
Aula 15 – 20.4.22 (vídeo) – Álgebra Exterior (vi): recapitulação – função determinante associada a uma base ordenada ortonormal. Formas de volume $p$ -dimensionais. O espaço vetorial das $p$ -formas num espaço vetorial: operações vetoriais pontuais, base de formas de volume $p$ -dimensionais gerada por uma base ordenada ortonormal. $p$ -vetores: definição, base de $p$ -vetores gerada por uma base ordenada ortonormal, $p$ -formas como funcionais lineares no espaço de $p$ -vetores.
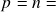Aula 14 – 14.4.22 (vídeo) – Álgebra Exterior (v): recapitulação – determinação de uma $p$ -forma por seus valores nos vetores de uma base numa determinada ordem, o caso $p=n=$ dimensão do espaço vetorial, bases ordenadas (definição, base associada, bases ordenadas ortogonais e ortonormais, a função determinante associada a uma base ordenada, determinação de uma $n$ -forma por seu valor numa base ordenada), Oodeterminante de uma transformação linear (definição e independência da base ordenada). Propriedades do determinante: determinante de uma matriz, adjunta e produto, critério do determinante para a invertibilidade de uma transformação linear. Orientação relativa de bases ordenadas, transformações lineares que preservam / invertem orientação. Volumes de paralelepípedos $n$ -dimensionais: a identidade de Lagrange $n$ -dimensional.
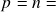Aula 13 – 13.4.22 (vídeo) – Álgebra Exterior (iv): recapitulação – determinação de uma $p$ -forma por seus valores nos vetores de uma base numa determinada ordem, o papel do sinal de um permutação dos argumentos de uma $p$ -forma. O caso $p=n=$ dimensão do espaço vetorial: bases ordenadas – definição, base associada, bases ordenadas ortogonais e ortonormais, a função determinante associada a uma base ordenada, determinação de uma $n$ -forma por seu valor numa base ordenada. O determinante de uma transformação linear: definição e independência da base ordenada.
Aula 12 – 6.4.22 (vídeo) – Álgebra Exterior (iii): recapitulação – expressão de uma $p$ -forma em termos de seus valores numa base, o caso de espaços vetoriais de dimensão finita. Interlúdio: permutações de $p$ elementos – definição, produto e inversão de permutações, o sinal de uma permutação (definição e propriedades básicas), transposições e seus sinais, decomposição de permutações como produtos de transposições. Determinação de uma $p$ -forma por seus valores nos vetores de uma base numa determinada ordem.
Aula 11 – 28.3.22 (reposição da aula de 24.3 – vídeo) – Álgebra Exterior (ii): recapitulação – $p$ -formas (definição algébrica e propriedades básicas = $p$ -linearidade e anti-simetria, caracterizações alternativas de anti-simetria de funções $p$ -lineares). Expressão de uma $p$ -forma em termos de seus valores numa base. O caso de espaços vetoriais de dimensão finita. Interlúdio: permutações de $p$ elementos – definição, produto e inversão de permutações, o sinal de uma permutação (definição e propriedades básicas).
Aula 10 – 25.3.22 (reposição da aula de 17.3 – vídeo) – Álgebra Exterior (i): motivação – áreas de paralelogramos, identidade de Lagrange, projeção ortogonal de paralelogramos. Relação do conceito de área com o conceito de determinante, sentido de varredura de área. $p$ -formas: definição algébrica e propriedades básicas ( $p$ -linearidade e anti-simetria). Caracterizações alternativas de anti-simetria de funções $p$ -lineares.
Aula 9 – 23.3.22 (vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (viii): o Teorema do Núcleo e da Imagem. Recapitulação – imagem e imagem inversa de subconjuntos por transformações lineares – definição, o caso de subespaços lineares, imagem e núcleo de uma transformação linear. O Teorema do Núcleo e da Imagem: enunciado, consequências (caracterização dimensional de sobrejetividade e injetividade de uma transformação linear, igualdade das dimensões do domínio e do contradomínio de uma transformação linear bijetora) e prova. Caracterização de sobrejetividade e injetividade de uma transformação linear por sua ação numa base do domínio. O Lema de Riesz e os isomorfismos musicais revisitados.
Aula 8 – 21.3.22 (reposição da aula de 16.3 – vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (vii): recapitulação – a matriz de uma transformação linear (determinação de uma transformação linear pelos seus valores numa base do domínio e suas componentes numa base do contradomínio = entradas da matriz de uma transformação linear num par de bases no domínio e contradomínio, vetores-coluna e a ação da matriz de uma transformação linear nestes, expressão das operações algébricas sobre transformações lineares em termos de operações análogas sobre matrizes). O efeito de mudanças de base sobre a matriz de uma transformação linear: matrizes de mudança de base, o caso de bases ortonormais. Imagem e imagem inversa de subconjuntos por transformações lineares – definição, o caso de subespaços lineares, imagem e núcleo de uma transformação linear. O Teorema do Núcleo e da Imagem (enunciado).
Aula 7 – 14.3.22 (reposição da aula de 10.3 – vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (vi): recapitulação – transformações lineares e 1-formas (definição e axiomas, exemplos simples, o espaço vetorial das transformações lineares entre dois espaços vetoriais, produtos = composições de transformações lineares, linearidade da inversa de uma transformação linear invertível). A matriz de uma transformação linear – determinação de uma transformação linear pelos seus valores numa base do domínio e suas componentes numa base do contradomínio = entradas da matriz de uma transformação linear num par de bases no domínio e contradomínio. Vetores-coluna e a ação da matriz de uma transformação linear nestes. Expressão das operações algébricas sobre transformações lineares (operações vetoriais pontuais, produto e inversão) em termos de operações análogas sobre matrizes. O caso de bases ortonormais – representação de transformações lineares e suas matrizes em termos de produtos escalares. Transposição de matrizes, a adjunta de uma transformação linear.
Aula 6 – 12.3.22 (reposição da aula de 3.3 – vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (v): transformações lineares – definição, axiomas e consequências. Funcionais lineares ( = 1-formas), espaços duais. Exemplos de transformações lineares (i): zero, múltiplos escalares, produto escalar com um vetor fixo ( = exemplo “genérico” de 1-forma – lema de Riesz). A estrutura de espaço vetorial do espaço de transformações lineares entre dois espaços vetoriais: operações vetoriais pontuais. O produto ( = composição) de transformações lineares: definição e propriedades algébricas (distributividade, associatividade e não-comutatividade). Linearidade da inversa de uma transformação linear.
Aula 5 – 9.3.22 (vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (iv): geometria do produto escalar – norma e distância euclidianas: definição e propriedades. A desigualdade de Cauchy-Schwarz para o produto escalar: enunciado, prova e consequências geométricas (desigualdade triangular para a norma e a distância euclidianas, ângulo entre vetores e lei dos cossenos). Caracterização geométrica de projeções ortogonais ao longo de um subespaço vetorial = vetor no subespaço mais próximo ao vetor dado.
Aula 4 – 24.2.22 (vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (iii): recapitulação – produtos escalares: o produto escalar canônico de Rn, axiomas do produto escalar, bases ortogonais e ortonormais, ortonormalização de Gram-Schmidt. Projeções ortogonais geradas por bases ortogonais e ao longo de subespaços vetoriais.
Aula 3 – 23.2.22 (vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (ii): produtos escalares – o produto escalar canônico de $\mathbb{R}^n$ , axiomas do produto escalar. Produtos escalares abstratos – definição. Produto escalar associado a uma base, bases ortogonais e ortonormais, ortonormalização de Gram-Schmidt.
Aula 2 – 17.2.22 (vídeo) – Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ (i): operações vetoriais e seus axiomas, subespaços vetoriais. Somatória vetorial, combinações lineares e (in)dependência linear. Bases e dimensão de subespaços vetoriais. Exemplos de subespaços vetoriais de $\mathbb{R}^n$ .
Aula 1 – 16.2.22 (vídeo) – Informações sobre a estrutura do curso. Motivação e objetivos: como seria uma versão do Teorema Fundamental do Cálculo para funções de várias variáveis? Campos vetoriais e fluxos – uma descrição informal.

Bibliografia

Listamos aqui os textos que seguiremos mais de perto.

Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969. Uma versão online gratuita dos dois volumes em inglês pode ser encontrada aqui).
Notas de aula serão disponibilizadas aqui à medida que o conteúdo for apresentado.

(Observação: o links do livro disponibilizado acima parte de um servidor que, em princípio, oferece tais materiais legalmente. Se for comprovado que este não é o caso, os links serão retirados sem aviso prévio)

Textos suplementares (listados na bibliografia das notas de aula):

R. Bott, L. Tu, Differential Forms in Algebraic Topology. Springer-Verlag, 1995.
R. W. R. Darling, Differential Forms and Connections. Cambridge University Press, 1994.
J. J. Duistermaat, J. A. C. Kolk, Multidimensional Real Analysis I – Differentiation; II – Integration. Cambridge University Press, 2004.
H. Flanders, Differential Forms with Applications to the Physical Sciences. Academic Press, 1963.
N. J. Hicks, Notes on Differential Geometry. Van Nostrand Reinhold, 1971.
E. L. Lima, Curso de Análise, Volume 2 (décima primeira edição). Projeto Euclides, IMPA, 2009.
L. Tu, An Introduction to Manifolds (2a. edição). Springer-Verlag, 2011.

Recomendações e material didático suplementar

Faremos uso tácito de conceitos vistos na disciplina BCN0407 – Funções de Várias Variáveis. Recomendamos fortemente que o aluno com dificuldades nos tópicos dessa disciplina faça uma revisão destes, pois isto não será feito em aula exceto nos casos previstos no Roteiro. Será feito também uso tácito de conceitos vistos na disciplina MCTB001 – Álgebra Linear, uma recapitulação dos quais pode ser encontrada na bibliografia básica indicada acima.

Estrutura das atividades da disciplina

As aulas a serem transmitidas sincronamente ocorrerão na seguinte data e horário semanais a partir de 16.2:

Quartas-feiras, 18h30-20h30.

Além disso, será gravada e disponibilizada assincronamente até o final do dia uma segunda aula semanal às quintas-feiras. Não haverá gravação ou transmissão de aulas em feriados – estes serão repostos no período de reposição seguindo o calendário acadêmico de 2022.

Reitero que a transmissão das aulas síncronas será gravada e disponibilizada posteriormente de maneira assíncrona. O link para a sala de reunião (Google Meet) onde cada aula será transmitida será divulgado por email e pelo Moodle com no máximo 30 minutos de antecedência por razões de segurança. A entrada nas salas de reunião só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de segurança e controle da participação dos alunos. Para realizar o vinculamento, recomendo seguir o tutorial do NTI para o procedimento.

O objetivo das aulas síncronas é permitir (dentro das limitações da internet de cada estudante e do docente) uma maior participação. Os links para os vídeos correspondentes a cada aula serão disponibilizados na lista de aulas.

Avaliação

A avaliação consistirá em dois tipos de atividades:

Duas provas (P₁, P₂) a serem aplicadas na plataforma Moodle, no seguinte formato: haverá uma janela temporal de 72 horas para a prova ser feita. Uma vez iniciada dentro desse período, o aluno terá até 3 horas para enviar a resolução (período suficiente para lidar com eventuais dificuldades no envio) ou até que a janela temporal se encerre (o que ocorrer primeiro).
Envio de resoluções de seleções de exercícios para cada uma das listas de exercícios (ver a seção “Listas de exercícios” abaixo para mais detalhes). As resoluções correspondentes a cada lista deverão também ser enviadas pelo Moodle dentro de uma janela temporal de 72 horas.

Haverá uma prova de recuperação a ser agendada para o início do segundo quadrimestre letivo de 2022, no mesmo formato que a P₁ e a P₂ mas que cobrirá o conteúdo do curso inteiro.

Média preliminar: M_p = 0,25*(P₁+P₂) + 0,5*M_l , onde M_l é a média simples das resoluções das listas de exercícios.

Média final: M_f = 0,25*max(P₁+P₂ ,Rec+P₁, Rec+P₂) + 0,5*M_l

Critério de conversão de média preliminar (M_p) / final (M_f) para conceito preliminar (C_p) / final (C_f):

C_p (resp. C_f) = F – M_p (resp. M_f) < 4,5;
C_p (resp. C_f) = D – M_p (resp. M_f) = 4,5-5,2;
C_p (resp. C_f) = C – M_p (resp. M_f) = 5,3-6,9;
C_p (resp. C_f) = B – M_p (resp. M_f) = 7,0-8,4;
C_p (resp. Cf) = A – M_p (resp. M_f) = 8,5-10,0.

Sugestões de ferramentas gratuitas para digitalização de documentos em formato PDF usando a câmera de smartphones:

Adobe Scan (Android, iOS);
vFlat (somente para Android);
Microsoft Office Lens (Android, iOS);
Google Drive (ferramenta de digitalização integrada à nuvem da Google – aviso: esse recurso é mais limitado que o dos apps dedicados listados acima! Somente para Android).

Janelas das provas:

P1 – 00h00 de terça-feira, 5.4 às 23h59 de quinta-feira, 7.4;
P2 – 00h00 de terça-feira, 10.5 às 23h59 de quinta-feira, 12.5;
Sub – 00h00 de terça-feira, 17.5 às 23h59 de quinta-feira, 19.5 (acessível apenas mediante apresentação de justificativa formal por escrito para a ausência na P1 ou P2);
Rec – a ser agendada no início do segundo quadrimestre letivo de 2022.

Janelas de envio de resoluções das listas de exercícios: a divulgar.

Durante cada janela de envio de resoluções de listas de exercícios, será aberta uma tarefa no Moodle com essa finalidade. Os detalhes sobre o envio das resoluções e as seleções de exercícios a serem resolvidos serão divulgados no início de cada janela.

Listas de exercícios

A serem divulgadas em breve.

É extremamente importante que os alunos façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!

Atendimento online e plantão de dúvidas

Haverá um plantão de dúvidas em videoconferência às terças-feiras das 19h00 às 21h00, usando a plataforma Google Meet, tal como a transmissão síncrona das aulas.

O plantão terá início em 22.2 – por razões de segurança, o link para a sala de reunião será divulgado por email e pelo Moodle no máximo 30 minutos antes do início de cada reunião.

Tal como na transmissão síncrona das aulas, a entrada nas salas de reunião dos plantões só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de controle da participação dos alunos.

Controle de frequência

A frequência será controlada mediante a participação nas aulas síncronas e nos plantões de dúvidas, bem como pela entrega das resoluções das seleções de exercícios das listas. Observo que, em virtude do caráter remoto das aulas, o controle de frequência não será usado para fins de reprovação por falta.

Roteiro

Seguiremos de maneira aproximada o cronograma sugerido para o curso de CVT pelo Gradmat, com algumas modificações na ordem e na ênfase – para uma descrição mais detalhada dos tópicos de cada aula, confira a lista das aulas. Alguns tópicos poderão ser omitidos, a depender do tempo disponível.

Uma breve revisão de Álgebra Linear em $\mathbb{R}^n$ : subespaços vetoriais e bases, produto escalar, norma e distância euclideanas, transformações lineares e mudanças de base.
Determinantes, multivetores e formas de volume orientadas associadas a uma base. Produto exterior. O efeito de mudanças de base sobre multivetores e formas de volume. Operador de Hodge sobre formas de volume, produto vetorial.
Análise vetorial: aplicações diferenciáveis e campos vetoriais, operadores gradiente, divergente, rotacional (em 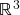$\mathbb{R}^3$ ) e laplaciano. Interpretação geométrica do gradiente. Formas diferenciais, derivada exterior e coderivada exterior. Operadores gradiente, divergente, rotacional e laplaciano revisitados.
Curvas, superfícies e subvariedades: caso parametrizado, cartas locais e descrição implícita, espaços tangentes / normais e campos vetoriais tangentes / normais. Parametrizações especiais: coordenadas polares, cilíndricas e esféricas.
Integrais de caminho, de superfície e em subvariedades. Caso parametrizado, mudança de variáveis e partições de unidade. (Ou: por que precisamos de formas de volume?)
Teorema Fundamental do Cálculo em várias variáveis: o teorema geral de Stokes. Casos particulares em duas e três dimensões: teoremas de Green, Gauss e Stokes clássico. Interpretação geométrica do divergente e do rotacional: fluxo e circulação de campos vetoriais. Interpretação geométrica do laplaciano: potencial de Newton e decomposição de Helmholtz de campos vetoriais em $\mathbb{R}^3$ .
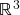Tópicos suplementares (se houver tempo): derivada covariante em subvariedades, geodésicas e curvatura, campos tensoriais. Aplicações à Física: fluidos, Eletromagnetismo e Relatividade.