Plano de ensino – TMI – 2q’23 – Pedro Lauridsen Ribeiro

Esta é a página sobre a disciplina MCTB020 – Teoria da Medida e Integração, ministrada no segundo quadrimestre de 2023 para a seguinte turma:

A1 – Noturno, campus Santo André – horário: 3as. feiras 19h00-21h00, sala A-S-008-0-SA e 6as. feiras 21h00-23h00, sala A-S-307-2-SA.

Aqui encontram-se informações específicas sobre a turma acima.

Novidades

Notícias recentes sobre o funcionamento do curso serão disponibilizadas aqui.

Aulas

Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.

Aula 6 – 20.6.23 – Interlúdio: relação de álgebras de subconjuntos com aneis booleanos e álgebras booleanas (ii) – propriedades básicas de aneis booleanos, teorema de representação de Stone.
Aula 5 – 16.6.23 – Álgebras e 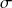$\sigma$ -álgebras de subconjuntos (ii): recapitulação – definição, espaços mensuráveis, consequências da definição. Interlúdio: relação de álgebras de subconjuntos com aneis booleanos e álgebras booleanas (i). Funções e aplicações mensuráveis (i): definição, imagem e imagem inversa de uma 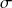$\sigma$ -álgebra de subconjuntos por uma aplicação mensurável.
Aula 4 – 13.6.23 – Álgebras e 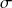$\sigma$ -álgebras de subconjuntos (ii): recapitulação – definição, espaços mensuráveis. Consequências da definição. Exemplos de 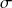$\sigma$ -álgebras num conjunto 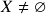$X\neq\varnothing$ : 1.) os casos triviais 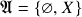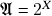$\mathfrak{A}=\{\varnothing,X\}$ , $\mathfrak{A}=2^X$ ; 2.) O caso 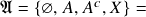$\mathfrak{A}=\{\varnothing,A,A^c,X\}=$ a menor 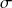$\sigma$ -álgebra em 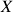$X$ contendo 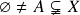$\varnothing\neq A\subsetneqq X$ – exemplo: subconjuntos pares e ímpares de 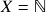$X=\mathbb{N}$ ; 3.) A 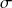$\sigma$ -álgebra gerada por uma família de subconjuntos de 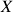$X$ – exemplos: 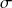$\sigma$ -álgebra de Borel em 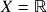$X=\mathbb{R}$ e num espaço métrico separável, 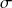$\sigma$ -álgebra de Borel num espaço topológico geral.
Aula 3 – 6.6.23 – Recapitulação: preliminares sobre operações conjuntísticas (uniões, interseções e complementos), diferença simétrica de dos subconjuntos, magem e imagem inversa de um subconjunto por uma função. Comportamento de imagens e imagens inversas de uniões, interseções e complementos. Álgebras e 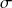$\sigma$ -álgebras de subconjuntos: definição, espaços mensuráveis.
Aula 2 – 2.6.23 – Preliminares sobre operações conjuntísticas. Uniões e interseções de famílias de subconjuntos: definição e propriedades (comutatividade, associatividade, idempotência, distributividade). Complementos: definição, propriedades, leis de de Morgan. O caso de famílias enumeráveis de subconjuntos: famílias monotonamente (re)crescentes, famílias mutuamente disjuntas, representação da união de uma família enumerável de subconjuntos como a união de uma família monotonamente crescente e a união de uma família mutuamente disjunta. Imagem e imagem inversa de um subconjunto por uma função: definição, imagem inversa de elementos no contradomínio, relação com sobrejetividade e injetividade.
Aula 1 – 30.5.23 – Informações sobre o funcionamento do curso. Motivação: a integral de Riemann e suas limitações – definição em termos de somas de Riemann com respeito a partições de um intervalo, integrais de Riemann impróprias, dificuldades com limites. Redefinindo a integral de Riemann em termos de funções escada. Estendendo a integral de Riemann: funções simples, partições mensuráveis de intervalos e funções simples mensuráveis. A integral com respeito a uma medida. Desafios: 1.) O que é uma medida e quais são os conjuntos mensuráveis? 2.) Quando uma função é integrável? 3.) A nova definição lida melhor com limites?

Bibliografia

Listamos aqui os textos que seguiremos mais de perto.

Robert G. Bartle, The Elements of Integration and Lebesgue Measure. Wiley, 1995.

Textos suplementares:

Steven Givant, Paul Halmos, Introduction to Boolean Algebras. Springer-Verlag, 2009.
Elliott H. Lieb, Michael Loss, Analysis (2a. edição). American Mathematical Society, 2001.
Walter Rudin, Real and Complex Analysis (3a. edição). McGraw-Hill, 1987.
Terence Tao: An Epsilon of Room, I: Real Analysis. American Mathematical Society, 2010.
Terence Tao: An Introduction to Measure Theory. American Mathematical Society, 2011.

Recomendações e material didático suplementar

Faremos uso tácito de conceitos vistos na disciplina MCTB006 – Análise Real II. Recomendamos fortemente que @ participante com dificuldades nesses tópicos faça uma revisão destes, pois isto não será feito em aula.

Avaliação

Média preliminar:
M_p = 0,5*(P₁+P₂)
Média final:
M_p = 0,5*max(P₁+P₂, Rec+P₁, Rec+P₂)
Critério de conversão de média preliminar (M_p) / final (M_f) para conceito preliminar (C_p) / final (C_f): C_p (resp. C_f) = F – M_p (resp. M_f) < 4,5;
C_p (resp. C_f) = D – M_p (resp. M_f) = 4,5-5,2;
C_p (resp. C_f) = C – M_p (resp. M_f) = 5,3-6,9;
C_p (resp. C_f) = B – M_p (resp. M_f) = 7,0-8,4;
C_p (resp. Cf) = A – M_p (resp. M_f) = 8,5-10,0.
Haverá uma prova substitutiva e uma prova de recuperação no final do curso. O conteúdo de ambas as provas compreenderá toda a matéria.
A prova substitutiva só poderá ser feita por participantes que não puderem comparecer a uma das provas, com justificativa formal por escrito da ausência entregue ao docente no máximo até o horário de início da prova substitutiva. Preferencialmente o documento original deve ser entregue; se não por possível (e.g. pelo mesmo ser exigido para justificar ausência em provas de outras disciplinas), será aceita uma cópia digitalizada enviada por email mas será exigido nesse caso que @ participante apresente o documento original para conferência dentro do mesmo prazo.
A prova de recuperação deverá ser aplicada pelo menos 72 horas após a divulgação dos conceitos finais, calculados após a aplicação da prova substitutiva (se houver necessidade de aplicar a última). Apenas participantes que ficaram com conceitos preliminares D e F (ver critério acima) após a aplicação da prova substitutiva poderão fazer essa prova. Haverá 15 minutos de tolerância para que @ participante que optar por fazer a prova de recuperação desista de fazê-lo.
Datas das provas:
P1 – 18.7 (terça-feira);
P2 – 22.8 (terça-feira);
Sub – 23.8 (quarta-feira, se houver necessidade – nesse caso, será agendada e divulgada em tempo hábil uma sala de aula para a Sub);
Rec – início do terceiro quadrimestre de 2023, a divulgar.
Como a data da P2 é destinada à reposição da ponte de feriado de 9.6 (Corpus Christi), essa prova seguirá os horários e locais da aula do dia da semana em que tenha caído o respectivo feriado sendo reposto. Ver calendário de reposição de feriados para mais detalhes.

Listas de exercícios

As listas de exercícios serão disponibilizadas aqui em breve.

Lista 1
Lista 2
Lista 3
Lista 4
Lista 5
Lista 6

É extremamente importante que @s participantes façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!

@s participantes que assim desejarem poderão entregar as suas resoluções das listas correspondentes à matéria de cada prova até a aula seguinte a prova correspondente (P1 – 21.7; P2 – data da Sub). Tais listas serão avaliadas nos casos de média final limítrofe para aprovação (ver tabela de conversão de conceitos acima), convertendo-se num bônus de até 1,5 ponto na média final.

Plantão de dúvidas

Haverá também um plantão de dúvidas por videoconferência (Google Meet) às segundas-feiras das 18h00 às 20h00, que terá início em 5.6. Para acessar a sala de reunião será necessário usar a conta Google vinculada ao endereço de email institucional da UFABC ((at)aluno.ufabc.edu.br). Veja o tutorial do NTI https://www.youtube.com/watch?v=Rf4kIbb4_sk para fazer a vinculação caso isso já não tenha sido feito. Reitero que o acesso à salaserá tacitamente negado a contas Google que não satisfaçam a essa condição, por razões de segurança. O link da sala será divulgado por email pouco antes do início de cada plantão.

Haverá também um fórum aberto de perguntas e respostas onde @s participantes poderão tirar suas dúvidas assincronamente com os monitores, os docentes e/ou colegas.

Roteiro

Preliminares de operações sobre conjuntos, imagens e imagens inversas, lim sup e lim inf. Espaços mensuráveis. Álgebras e 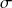$\sigma$ -álgebras de conjuntos mensuráveis. Funções e aplicações mensuráveis.
Medidas num espaço mensurável. Medidas exteriores, critério de Carathéodory para conjuntos mensuráveis a partir de uma medida exterior, teorema de extensão de Carathéodory.
Construção de medidas exteriores, teorema de extensão de Hahn. Medidas de Borel e de Lebesgue na reta real e no $\mathbb{R}^n$ .
Integração. A função distribuição de uma função mensurável com respeito a uma medida e representação em camadas da integral. Teoremas de convergência (monótona, de Fatou e dominada). Medidas produto, teorema de Fubini.
Noções básicas de espaços 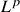$L^p$ , desigualdades de Hölder e de Minkowski. Dualidade.
Modos de convergência: convergência em 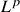$L^p$ , convergência em medida e convergência quase uniforme.