
Esta é a página sobre a disciplina BCN0405 – Introdução às Equações Diferenciais Ordinárias, ministrada no terceiro quadrimestre de 2025 para a seguinte turma:
- B1 – Noturno, campus Santo André – horário: 2as. feiras 21h00-23h00 e 4as. feiras 19h00-21h00, sala A-S204-0-SA.
Aqui encontram-se informações específicas sobre a turma acima – informações gerais sobre o curso podem ser encontradas na página do Gradmat para a disciplina de IEDO.
Aulas
Uma breve descrição do conteúdo apresentado em cada aula está listada abaixo.
- Aula 20 – 1.12.25 – Aplicações a sistemas mecânicos e elétricos (iii): recapitulação – condições físicas sobre os coeficientes de uma EDO linear de segunda ordem com coeficientes constantes e suas consequências sobre o comportamento qualitativo da solução geral (i) no caso homogêneo – regimes de amortecimento (subcrítico, crítico e supercrítico), fator de amortecimento e decaimento temporal (comportamento transiente) da solução geral, frequência natual (de oscilação na ausência de amortecimento) e quase-frequência de oscilação (no regime subcrítico). O caso (ii) não-homogêneo: fontes constantes e senoidais, amplitude, frequência (angular) de oscilação e fase de uma função senoidal, solução particular (pelo método de coeficientes indeterminados) no caso em qua fonte não é solução da EDO linear homogênea associada – amplitude e fase em função da frequência da fonte, pico de amplitude na frequência natural do sistema (ressonância com amortecimento) e atraso de fase. O caso em que a fonte é solução da EDO linear homogênea associada (ressonância sem amortecimento): solução particular com amplitude crescendo linearmente com o tempo, atraso de fase de
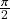 radianos. (Boyce-DiPrima: Seções 3.7 e 3.8; Zill: Seção 5.1)
radianos. (Boyce-DiPrima: Seções 3.7 e 3.8; Zill: Seção 5.1) - Aula 19 – 26.11.25 – Aplicações a sistemas mecânicos e elétricos (ii): recapitulação – construção da EDO descrevendo um sistema massa-mola sujeito à resistência (linear) do ar e a uma força externa e da EDO descrevendo a carga / corrente elétrica num circuito LRC. Condições físicas sobre os coeficientes da EDO e suas consequências sobre o comportamento qualitativo da solução geral (i): caso homogêneo – regimes de amortecimento (subcrítico, crítico e supercrítico), fator de amortecimento e decaimento temporal (comportamento transiente) da solução geral, frequência natual (de oscilação na ausência de amortecimento) e quase-frequência de oscilação (no regime subcrítico). (Boyce-DiPrima: Seções 3.7 e 3.8; Zill: Seção 5.1)
- Aula 18 – 24.11.25 – Método de coeficientes indeterminados (ii): recapitulação – formulação geral e exemplos. O caso em que a fonte é solução da EDO linear homogênea associada, ajustes no método. Aplicações a sistemas mecânicos e elétricos (i): construção da EDO descrevendo um sistema massa-mola sujeito à resistência (linear) do ar e a uma força externa e da EDO descrevendo a carga / corrente elétrica num circuito LRC (Boyce-DiPrima: Seções 3.5, 3.7 e 3.8; Zill: Seções 4.4, 4.6 e 5.1)
- Aula 17 – 19.11.25 – Solução particular de EDO’s lineares não-homogêneas de segunda ordem com coeficientes constantes (ii): recapitulação – método de variação de parâmetros, solução com dados iniciais zero e solução geral, fixando os coeficientes da função complementar ( = combinação linear genérica dos membros de uma base de soluções da EDO linear homogênea associada) em termos dos dados iniciais. Método de coeficientes indeterminados (i): formulação geral e exemplos, o caso em que a fonte é solução da EDO linear homogênea associada. (Boyce-DiPrima: Seções 3.5 e 3.6; Zill: Seções 4.4 e 4.6)
- Aula 16 – 17.11.25 – Solução particular de EDO’s lineares não-homogêneas de segunda ordem com coeficientes constantes (i): método da variação de parâmetros. Recapitulação – solução geral de EDO’s lineares homogêneas de segunda ordem com coeficientes constantes (soluções exponenciais, polinômio característico e suas raízes, classificação da solução geral em termos do discriminante do polinômio característico). Formulação do método de variação de parâmetros: o exemplo de EDO’s lineares de primeira ordem e relação com o método do fator integrante, solução particular de uma EDO linear não-homogênea de segunda ordem com coeficientes constantes em termos de uma base de soluções da EDO linear homogênea associada, o papel do Wronskiano, solução particular com dados iniciais zero. (Boyce-DiPrima: Seções 3.1 a 3.4 e 3.6; Zill: Seções 4.3 e 4.6)
- Aula 15 – 12.11.25 – EDO’s lineares homogêneas de segunda ordem (ii): solução geral no caso de coeficientes constantes – soluções exponenciais, polinômio característico e suas raízes. Classificação das bases de soluções de acordo com o sinal do discriminante do polinômio característico: 1.) discriminante positivo ( = raízes reais e distintas)
 duas soluções exponenciais linearmente inependentes; 2.) discriminante zero ( = uma única raiz (real))
duas soluções exponenciais linearmente inependentes; 2.) discriminante zero ( = uma única raiz (real))  uma solução exponencial, obtenção de uma segunda solução pelo método de redução de ordem; 3.) discriminante negatico ( = sem raízes reais)
uma solução exponencial, obtenção de uma segunda solução pelo método de redução de ordem; 3.) discriminante negatico ( = sem raízes reais)  soluções linearmente independentes como produtos de exponenciais e funções trigonométricas. Interpretação da base de soluções no caso 3.) como partes real e imaginária de exponenciais complexas. Solução particular de EDO’s lineares não-homogêneas de segunda ordem com coeficientes constantes (i): método da variação de parâmetros. (Boyce-DiPrima: Seções 3.1 a 3.4; Zill: Seções 4.3 e 4.6)
soluções linearmente independentes como produtos de exponenciais e funções trigonométricas. Interpretação da base de soluções no caso 3.) como partes real e imaginária de exponenciais complexas. Solução particular de EDO’s lineares não-homogêneas de segunda ordem com coeficientes constantes (i): método da variação de parâmetros. (Boyce-DiPrima: Seções 3.1 a 3.4; Zill: Seções 4.3 e 4.6) - Aula 14 – 10.11.25 – EDO’s lineares de ordem superior (ii): recapitulação – Princípio de Superposição: caso não-homogêneo (a diferença entre duas soluções de uma EDO linear é solução da EDO linear homogênea associada + a soma de uma solução de uma EDO com uma solução da EDO linear homogênea associada é também solução da EDO linear original), caso homogêneo (somas e múltiplos constantes de soluções de uma EDO linear homogênea tambẃm são soluções). Soluções linearmente independentes e bases ( = conjuntos fundamentais) de soluções de uma EDO linear homogênea, forma da solução geral de uma EDO linear de ordem
 = solução particular da EDO + combinação linear de
= solução particular da EDO + combinação linear de  soluções linearmente independentes da EDO linear homogênea associada (função complementar). O Wronskiano de um conjunto de
soluções linearmente independentes da EDO linear homogênea associada (função complementar). O Wronskiano de um conjunto de  soluções de uma EDO linear homogênea de ordem
soluções de uma EDO linear homogênea de ordem  : EDO linear de primeira ordem associada, critério de independência linear. EDO’s lineares homogêneas de segunda ordem (i): obtenção de uma solução linearmente independente a partir de uma solução dada (método de abaixamento de ordem). (Boyce-DiPrima: Seções 3.1 e 3.2; Zill: Seções 4.1 e 4.2)
: EDO linear de primeira ordem associada, critério de independência linear. EDO’s lineares homogêneas de segunda ordem (i): obtenção de uma solução linearmente independente a partir de uma solução dada (método de abaixamento de ordem). (Boyce-DiPrima: Seções 3.1 e 3.2; Zill: Seções 4.1 e 4.2) - Aula 13 – 5.11.25 – Errata da Aula 12 – equação de Riccati. EDO’s lineares de ordem superior (i): preliminares – existência e unicidade de soluções do problema de valor inicial para EDO’s lineares de ordem
 a partir do Teorema de Existência e Unicidade (de Picard-Lindelöf). Princípio de Superposição – caso não-homogêneo (a diferença entre duas soluções de uma EDO linear é solução da EDO linear homogênea associada + a soma de uma solução de uma EDO com uma solução da EDO linear homogênea associada é também solução da EDO linear original), caso homogêneo (somas e múltiplos constantes de soluções de uma EDO linear homogênea tambẃm são soluções). Consequências do Princípio de Superposição para o problema de valor inicial para uma EDO linear – soluções linearmente independentes e base de soluções de uma EDO linear homogênea, forma da solução geral de uma EDO linear de ordem
a partir do Teorema de Existência e Unicidade (de Picard-Lindelöf). Princípio de Superposição – caso não-homogêneo (a diferença entre duas soluções de uma EDO linear é solução da EDO linear homogênea associada + a soma de uma solução de uma EDO com uma solução da EDO linear homogênea associada é também solução da EDO linear original), caso homogêneo (somas e múltiplos constantes de soluções de uma EDO linear homogênea tambẃm são soluções). Consequências do Princípio de Superposição para o problema de valor inicial para uma EDO linear – soluções linearmente independentes e base de soluções de uma EDO linear homogênea, forma da solução geral de uma EDO linear de ordem  ( = solução particular da EDO + combinação linear de
( = solução particular da EDO + combinação linear de  soluções linearmente independentes da EDO linear homogênea associada). (Boyce-DiPrima: Seções 3.1 e 3.2; Zill: Seção 4.1)
soluções linearmente independentes da EDO linear homogênea associada). (Boyce-DiPrima: Seções 3.1 e 3.2; Zill: Seção 4.1) - Aula 12 – 3.11.25 – Existência e unicidade de soluções do problema de valor inicial para EDO’s: fundamentos teóricos. Contra-exemplos para unicidade (EDO
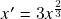 com condição inicial zero) e intervalos de existência arbitrariamente curtos (EDO de Riccati). Teoremas de Existência e Unicidade para sistemas de EDO’s de primeira ordem na forma normal: teoremas de Picard-Lindelöf (existência e unicidade) e de Cauchy-Peano (existência com possível quebra de unicidade). Condições suficientes para a validade das hipóteses do Teorema de Picard-Lindelöf (
com condição inicial zero) e intervalos de existência arbitrariamente curtos (EDO de Riccati). Teoremas de Existência e Unicidade para sistemas de EDO’s de primeira ordem na forma normal: teoremas de Picard-Lindelöf (existência e unicidade) e de Cauchy-Peano (existência com possível quebra de unicidade). Condições suficientes para a validade das hipóteses do Teorema de Picard-Lindelöf (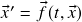 ,
, 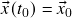 tem uma única solução num intervalo de existência pequeno o suficiente se
tem uma única solução num intervalo de existência pequeno o suficiente se 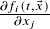 são contínuas). Redução de problemas de valor inicial para EDO’s de ordem superior e seus sistemas (resp. na forma normal) ao caso de sistemas de EDO’s de primeira ordem (resp. na forma normal), existência e unicidade de soluções. (Boyce-DiPrima: Seção 2.4; Zill: Seção 1.2)
são contínuas). Redução de problemas de valor inicial para EDO’s de ordem superior e seus sistemas (resp. na forma normal) ao caso de sistemas de EDO’s de primeira ordem (resp. na forma normal), existência e unicidade de soluções. (Boyce-DiPrima: Seção 2.4; Zill: Seção 1.2) - Aula 11 – 22.10.25 – Modelagem matemática por EDO’s de primeira ordem: roteiro geral de modelagem matemática de fenômenos naturais – 1.) construção do modelo ( = EDO de primeira ordem, no nosso caso), variáveis independentes, variáveis dependentes, parâmetros e seu domínio de validade; 2.) solução do modelo (problema matemático abstrato) obitdo no passo 1.) ( = solução do PVI para a EDO, no nosso caso) dentro do seu domínio de validade; 3.) interpretação da solução do modelo no contexto do fenômeno, predições teóricas; 4.) validação do modelo por dados empíricos e posterior aprimoramento do modelo obtido no passo 1.). Exemplos de modelos matemáticos por EDO’s de primeira ordem (passos 1.) – 3.)): (a) lei de decimento radioativo; (b) lei de resfriamento de Newton. (Boyce-DiPrima: Seção 2.3; Zill: Seções 1.3, 3.1 e 3.2)
- Aula 10 – 20.10.25 – Análise qualitativa de EDO’s autônomas (ii): recapitulação – pontos de equilíbrio e soluções de equilíbrio. Invariância translacional do espaço de soluções, forma qualitativa das soluções de uma EDO autônoma com dados iniciais entre dois pontos de equilíbrio sucessivos. Classificação dos pontos de equilíbrio em termos de sua estabilidade (pontos de equilíbrio estáveis, instáveis e semiestáveis por baixo / por cima no futuro / passado). Exemplos (EDO logística = EDO de Verhulst). Retrato de fase (esboço) do espaço de soluções. (Boyce-DiPrima: Seção 2.5; Zill: Seção 2.1)
- Aula 9 – 15.10.25 – Análise qualitativa de EDO’s autônomas (i): pontos de equilíbrio e soluções de equilíbrio. Forma qualitativa das soluções de uma EDO autônoma com dados iniciais entre dois pontos de equilíbrio sucessivos. Classificação dos pontos de equilíbrio em termos de sua estabilidade: pontos de equilíbrio estáveis, instáveis e semiestáveis por baixo / por cima no futuro / passado. (Boyce-DiPrima: Seção 2.5; Zill: Seção 2.1).
- Aula 8 – 13.10.25 – Método de substituição (ii): recapitulação – formulação geral com dependência explícita na variável independente, solução de EDO’s da forma
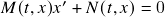 com
com 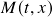 ,
, 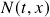 homogêneas de grau
homogêneas de grau 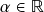 (redução a uma EDO separável), solução explícita no caso linear. Análise qualitativa de EDO’s autônomas (i): pontos de equilíbrio e soluções de equilíbrio. (Boyce-DiPrima: Seção 2.5; Zill: Seção 2.5)
(redução a uma EDO separável), solução explícita no caso linear. Análise qualitativa de EDO’s autônomas (i): pontos de equilíbrio e soluções de equilíbrio. (Boyce-DiPrima: Seção 2.5; Zill: Seção 2.5) - Aula 7 – 8.10.25 – Método de substituição (ii): formulação geral, solução da equação de Bernoulli (redução a uma EDO linear). Extensão do método de substituição para incluir dependência explícita na variável independente, solução de EDO’s da forma
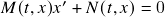 com
com 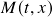 ,
, 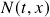 homogêneas de grau
homogêneas de grau 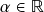 (redução a uma EDO separável), solução explícita no caso linear. (Zill: Seção 2.5)
(redução a uma EDO separável), solução explícita no caso linear. (Zill: Seção 2.5) - Aula 6 – 6.10.25 – EDO’s exatas (ii): recapitulação – derivação implícita, condições de integrabilidade, recuperação da equação de função implícita satisfeita pelas soluções do problema de valor inicial para uma EDO exata. Fator integrante e condições de integrabilidade generalizadas para EDO’s de primeira ordem não-exatas, os casos de EDO’s lineares e EDO’s separáveis (na forma normal). Método de substituição (i): formulação geral e exemplos (equação de Bernoulli). (Boyce-DiPrima: Seções 2.4 e 2.6; Zill: Seções 2.4 e 2.5)
- Aula 5 – 1.10.25 – Recapitulação: solução do problema de valor inicial para EDO’s lineares de primeira ordem reduzidas à forma normal lineares (método do fator integrante) e (com variáveis) separáveis. O caso autônomo de EDO’s separáveis de primeira ordem ( = EDO’s de primeira ordem autônomas gerais na forma normal). EDO’s exatas (i): motivação (derivação implícita), condições de integrabilidade, recuperação da equação de função implícita satisfeita pelas soluções do problema de valor inicial para uma EDO exata. (Boyce-DiPrima: Seções 2.1, 2.2 e 2.6; Zill: Seções 2.2 a 2.4)
- Aula 4 – 29.9.25 – Recapitulação: EDO’s de primeira ordem (ii): forma normal, solução do problema de valor inicial para EDO’s lineares de primeira ordem reduzidas à forma normal – o caso da EDO para uma primitiva (Teorema Fundamental do Cálculo) e o caso homogêneo (derivadas logarítmicas), método do fator integrante. Verificação de que as fórmulas obtidas pelo método do fator integrante são de fato soluções, fórmula explícita no caso autônomo. EDO’s de primeira ordem (com variáveis) separáveis: estratégia básica de solução, verificação de que a fórmula obtida de fato é uma solução. (Boyce-DiPrima: Seções 1.2, 2.1 e 2.2; Zill: Seções 1.2, 2.2 e 2.3)
- Aula 3 – 22.9.25 – Recapitulação: famílias (parametrizadas) de soluções, solução geral de uma EDO. Casos particulares: parametrização por valores iniciais e valores de contorno. Problemas de valor inicial (PVI’s), problemas (de valores) de contorno (PVC’s) e sua boa postura ( = existência e unicidade de soluções para cada escolha de condições iniciais / de contorno), necessidade do número de condições iniciais / de contorno independentes ser igual à ordem da EDO. EDO’s de primeira ordem (i): forma normal, solução do problema de valor inicial para EDO’s lineares de primeira ordem reduzidas à forma normal – o caso da EDO para uma primitiva (Teorema Fundamental do Cálculo) e o caso homogêneo (derivadas logarítmicas), método do fator integrante. (Boyce-DiPrima: Seções 1.2 e 2.1; Zill: Seções 1.2 e 2.3)
- Aula 2 – 17.9.25 – Recapitulação: EDO’s e suas soluções, terminologia básica, EDO’s (a valores) vetoriais e sistemas de EDO’s. Classificação de EDO’s – classificação por ordem, EDO’s autônomas e não-autônomas, EDO’s lineares e não-lineares. Classificação de EDO’s lineares em termos de seus coeficientes: coeficientes constantes e variáveis, EDO’s lineares homogêneas e não-homogêneas. Exemplos. Extensão da classificação de EDO’s para EDO’s vetoriais e sistemas de EDO’s, redução de uma EDO de ordem
 a um sistema de
a um sistema de  EDO’ s de primeira ordem. Famílias (parametrizadas) de soluções, solução geral de uma EDO. (Boyce-DiPrima: Seções 1.2 e 1.3; Zill: Seções 1.1 e 1.3)
EDO’ s de primeira ordem. Famílias (parametrizadas) de soluções, solução geral de uma EDO. (Boyce-DiPrima: Seções 1.2 e 1.3; Zill: Seções 1.1 e 1.3) - Aula 1 – 15.9.25 – Informações sobre o funcionamento do curso. Motivação: o que são equações diferenciais ordinárias (EDO’s), e para que servem? EDO’s e suas soluções, terminologia básica, EDO’s vetoriais e sistemas de EDO’s. EDO’s como modelos matemáticos de leis naturais – exemplos (Segunda Lei de Newton, circuitos elétricos, decaimento radioativo), interpretação dos parâmetros de uma EDO no contexto de um modelo. (Boyce-DiPrima: Seção 1.3; Zill: Seções 1.1 e 1.3)
Bibliografia
Listamos aqui os textos que seguiremos mais de perto.
- William E. Boyce, Richard C. DiPrima, Equações Diferenciais Elementares e Problemas de Valores de Contorno (10a. edição). Editora LTC, 2015 (original em inglês: Elementary Differential Equations and Boundary Value Problems – Tenth Edition. Wiley, 2012). Exemplares podem ser encontrados na biblioteca do campus Santo André (link acessível somente dentro do campus).
- Constantin Corduneanu, Principles of Differential and Integral Equations (AMS Chelsea, 1977).
- Hamilton L. Guidorizzi, Um Curso de Cálculo, Volume 4 (5a. edição). Editora LTC, 2002.
- Dennis G. Zill, Equações Diferenciais com Aplicações em Modelagem (10a. edição). Cengage Learning, 2016 (original em inglês: A First Course in Differential Equations with Modelling Applications – Tenth Edition. Cengage Learning, 2012). Exemplares podem ser encontrados na biblioteca do campus Santo André (link acessível somente dentro do campus).
Textos suplementares:
- Tom M. Apostol, Cálculo, Volume 1 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume I – Second Edition. Wiley, 1967); Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969).
- James Stewart, Cálculo, Volume 2 (6a. edição). Cengage Learning, 2010.
- Armando Caputi, Cristian F. Coletti e Daniel Miranda – Notas de Aula de Cálculo I (online) – referência suplementar para o material de FUV empregado no curso de IEDO.
- Rodney Bassanezzi – Equações Diferenciais Ordinárias (online em formato PDF).
- J. C. A. Barata, Curso de Física-Matemática (online em formato PDF) – Capítulos 12 (Equações Diferenciais Ordinárias. Uma Introdução), 13 (Alguns Métodos de Resolução de Equações Diferenciais Ordinárias) e 14 (Sistemas de Equações Diferenciais Ordinárias Lineares).
(Observação: os links dos livros disponibilizados acima partem de um servidor que, em princípio, oferece tais materiais legalmente. Se for comprovado que este não é o caso, os links serão retirados sem aviso prévio)
Recomendações e material didático suplementar
Faremos uso tácito dos conceitos vistos na disciplina BCN0402 – Funções de Uma Variável e, em menor grau, de conceitos vistos na disciplina BCN0407 – Funções de Várias Variáveis. Uma breve recapitulação do teorema fundamental do Cálculo será feita numa das aulas, à guisa de motivação (ver Roteiro abaixo para mais detalhes), e uma breve revisão de técnicas de diferenciação e integração pode ser encontrada na Lista 0 de exercícios (ver Listas de exercícios abaixo para mais detalhes). Haverá também uma revisão similar no Teste online 0 (ver Testes online (Moodle) abaixo para mais detalhes). Os tópicos de FVV relevantes para IEDO (cálculo diferencial de várias variáveis, até a Regra da Cadeia e funções implícitas) não serão revisados em aula, então recomendamos fortemente que o aluno com dificuldades nestes faça uma revisão. Estarei à disposição para atender dúvidas referentes às recomendações nos plantões de dúvidas.
Uma seleção de vídeos para estudo individual pode ser encontrada na página do Gradmat para a disciplina de IEDO.
Para auxiliar o estudo individual de resolução de EDO’s, recomendamos o software Symbolab. Para mais sugestões de software, recomendamos visitar a página do Gradmat para a disciplina de IEDO.
Avaliação
- Média preliminar:
Mp = 0,3*(P1+P2) + 0,4*Mt, onde Mt é a média dos testes online no Moodle (valendo de 0 a 10). - Média final:
Mp = 0,3*max(P1+P2, Rec+P1, Rec+P2) + 0,4*Mt - Critério de conversão de média preliminar (Mp) / final (Mf) para conceito preliminar (Cp) / final (Cf): Cp (resp. Cf) = F – Mp (resp. Mf) < 4,5;
Cp (resp. Cf) = D – Mp (resp. Mf) = 4,5-5,2;
Cp (resp. Cf) = C – Mp (resp. Mf) = 5,3-6,9;
Cp (resp. Cf) = B – Mp (resp. Mf) = 7,0-8,4;
Cp (resp. Cf) = A – Mp (resp. Mf) = 8,5-10,0. - Haverá uma prova substitutiva e uma prova de recuperação no final do curso. O conteúdo de ambas as provas compreenderá toda a matéria.
- A prova substitutiva só poderá ser feita por participantes que não puderem comparecer a uma das provas, com justificativa formal por escrito da ausência entregue ao docente no máximo até o horário de início da prova substitutiva. Preferencialmente o documento físico original e/ou digital com assinatura digital deve ser entregue; se não por possível (e.g. pelo documento original ser exigido para justificar ausência em provas de outras disciplinas), será aceita uma cópia digitalizada enviada por email mas será exigido nesse caso que @ participante apresente o documento original para conferência dentro do mesmo prazo.
- A prova de recuperação será aplicada no início do 1q’26, em data e local a serem divulgados futuramente. Apenas participantes que ficaram com conceitos preliminares D e F (ver critério acima) após a aplicação da prova substitutiva poderão fazer essa prova.
- Datas das provas:
P1 – 29.10 (quarta-feira);
P2 – 3.12 (quarta-feira);
Sub – 8.12 (segunda-feira, se houver necessidade);
Rec – início do primeiro quadrimestre de 2026, a divulgar.
Listas de exercícios
As listas de exercícios do Gradmat podem ser encontradas aqui:
É extremamente importante que @s participantes façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!
@s participantes que assim desejarem poderão entregar as suas resoluções das listas correspondentes à matéria de cada prova até a aula seguinte a prova correspondente (P1 – 3.11; P2 – data da Rec). Tais listas serão avaliadas nos casos de média final limítrofe para aprovação (ver tabela de conversão de conceitos acima), convertendo-se num bônus de até 1,5 ponto na média final.
Testes online (Moodle)
Haverá quatro (4) testes online na plataforma Moodle. @s participantes deverão receber as informações detalhadas sobre cada teste diretamente nos seus emails institucionais ((at)aluno.ufabc.edu.br), e deverão logar-se na plataforma com seu login e senha institucionais para fazer os testes.
Os exercícios cobertos nos testes online constituem uma seleção mínima de exercícios e não substituem a resolução das listas de exercícios do Gradmat, que são mais abrangentes e completas.
Cronograma de janelas de resolução dos testes:
- Teste 1 – 11.10 a 14.10;
- Teste 2 – 25.10 a 28.10;
- Teste 3 – 15.11 a 18.11;
- Teste 4 – 29.11 a 2.12.
Monitoria e plantão de dúvidas
A partir de terça-feira, 23.9 haverá atendimento presencial pelo monitor Artur Sobral Paulo nas seguintes datas e horários:
- Terças-feiras, 14h00-15h30, sala B-S502 (campus SA);
- Quintas-feiras, 17h30-19h00, sala B-S502 (campus SA).
O monitor fará também atendimento online assíncrono no Telegram e no Discord. Por motivos de segurança, as informações de contato do monitor tem acesso restrito ao Moodle.
Haverá um plantão de dúvidas às segundas-feiras das 17h00 às 19h00, na minha sala (A-S543-2, Torre 2, Bloco A, campus Santo André). O plantão terá início no dia 22.9.
Roteiro
Seguiremos de maneira aproximada o cronograma unificado sugerido para a disciplina de IEDO, com algumas modificações a serem indicadas quando necessário.
- Motivação e terminologia básica, EDO’s como modelos matemáticos de leis naturais. Soluções particulares e gerais, dados iniciais e de contorno, problemas de valor inicial e de contorno, classificação de EDO’s.
- EDO’s de primeira ordem. O teorema fundamental do cálculo como a solução da EDO mais simples. Técnicas particulares de solução: EDO’s exatas, curvas integrais e campos tangentes; EDO’s separáveis; EDO’s autônomas e homogêneas; simplificação por substituição: equações de Bernoulli e de Riccati, equação de Clairaut, redução de ordem.
- EDO’s lineares de primeira ordem. Solução geral: método do fator integrante e método da variação das constantes. Modelos (construção e solução).
- EDO’s autônomas de primeira ordem. Modelos (construção e solução). Análise qualitativa: pontos de equilíbrio, estabilidade e assíntotas.
- Teoremas gerais de existência e unicidade de soluções de EDO’s. Enunciado e consequências.
- EDO’s lineares de segunda ordem. EDO’s lineares homogêneas com coeficientes constantes, o wronskiano.
- Métodos de solução de EDO’s lineares de segunda ordem: método dos coeficientes indeterminados e método de variação das constantes.
- EDO’s lineares de segunda ordem. Modelos: sistemas mecânicos e elétricos, oscilações forçadas e ressonância.
- Sistemas de EDO’s lineares. Redução a EDO’s de primeira ordem.
- EDO’s de ordem superior (se houver tempo).

