
Esta é a página sobre a disciplina MCTB010 – Cálculo Vetorial e Tensorial, ministrada no primeiro quadrimestre de 2020 para as seguintes turmas:
- A1 – Noturno, campus Santo André – horário: 4as. feiras 19h00-21h00 e 6as. feiras 21h00-23h00, sala A-S204-0-SA.
- B1 – Noturno, campus Santo André – horário: 4as. feiras 21h00-23h00 e 6as. feiras 19h00-21h00, sala A-S204-0-SA.
Aqui encontram-se informações específicas sobre as turmas acima.
Importante! Para informações sobre o curso posteriores a 6.4.20, ver o plano de ensino no formato ECE.
Novidades:
Notícias recentes sobre o funcionamento do curso serão disponibilizadas aqui.
- (6.4.20) Atenção: devido à adesão ao formato de Estudos Continuados Emergenciais (ECE), esta página não será mais atualizada a partir de amanhã (terça-feira, 7.4).
- (20.3.20) Preparei um questionário sobre a viabilidade e a estrutura das atividades online para a disciplina, particularmente no que concerne o acesso à Internet fora da Universidade por parte dos alunos. Os resultados serão usados para finalizar o planejamento da nova estrutura do curso, em acordo com as diretrizes institucionais a serem determinadas pela UFABC para as atividades acadêmicas durante o período de suspensão. O questionário está aberto para preenchimento até as 23h59 da próxima quinta-feira, 26.3. Por favor, quem tiver acesso à Internet fora da Universidade, mesmo que seja só excepcionalmente para preencher o questionário acima, não deixe de fazê-lo pois isso servirá também para medir o grau de acesso das turmas a esse recurso.
- (18.3.20) Hoje a Reitoria da UFABC estendeu o período de suspensão das atividades acadêmicas e administrativas nos dois campi até 29 de março.
- (17.3.20) Primeiro boletim sobre a nova estrutura do curso: devido à necessidade de planejamento por parte da coordenação da disciplina de CVT neste quadrimestre letivo para todas as turmas, as aulas e provas estarão suspensas até (inclusive) sexta-feira, 27.3. O detalhamento da nova estrutura do curso para as turmas A1 Noturno e B1 Noturno (campus Santo André) será comunicado aqui até quarta-feira, 25.3.
- (13.3.20) Importante: devido ao momento atual da pandemia de coronavírus (COVID-19) na Grande São Paulo, a Reitoria da UFABC emitiu um comunicado às 19h50 de hoje suspendendo as atividades acadêmicas e administrativas nos dois campi de 16 a 22 de março. A suspensão poderá ou não ser prorrogada a depender da evolução do número de casos. Em vista disso, a disciplina será migrada para um formato online – os detalhes da nova estrutura do curso (aulas, avaliação, plantões de dúvidas) serão comunicados aqui até terça-feira, 17.3. Por ora, as datas e formato das provas restantes (P2-P5, Sub, Rec) estão suspensas para reavaliação à luz dessa nova estrutura.
- (11.3.20) A P2 será adiada para sexta-feira, 20.3 devido ao atraso na disponibilização da lista 2. O conteúdo da P2 corresponde a essa lista, abrangendo as aulas 5 a 8. As datas das demais provas permanecem inalteradas.
- (11.3.20) A segunda versão das notas de aula está disponível, cobrindo as aulas 1 a 8. Comentários, sugestões e correções são bem-vindos. A lista 2 será disponibilizada até quinta-feira, 9.4.
- (4.3.20) As notas da P1 serão divulgadas até quinta-feira, 9.4.
- (23.2.20) A matéria da P1 corresponde ao conteúdo da Lista 1.
- (23.2.20) A Lista 1 está disponível. Por favor, não deixar de reportar eventuais erros nos enunciados e/ou no gabarito da lista.
- (23.2.20) A primeira versão das notas de aula está disponível, cobrindo as aulas 1 a 4. Comentários, sugestões e correções são bem-vindos.
- (21.2.20) Para evitar colisões com os horários de monitoria presencial, o horário do plantão de dúvidas das quintas-feiras passará a ser das 19h00 às 20h30 a partir de 27.2.
- (19.2.20) Os plantões de monitoria presencial começarão amanhã (quinta-feira, 20.2). Os horários e locais de atendimento podem ser encontrados na página de monitoria de CVT do Gradmat (ver também a seção “Monitoria, atendimento online e plantão de dúvidas” abaixo).
Bibliografia:
Listamos aqui os textos que seguiremos mais de perto.
- Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969. Uma versão online gratuita dos dois volumes em inglês pode ser encontrada aqui).
- Hamilton L. Guidorizzi, Um Curso de Cálculo, Volume 3 (5a. edição). Editora LTC, 2001.
- James Stewart, Cálculo, Volume 2 (6a.,edição). Cengage Learning, 2012.
- Notas de aula serão disponibilizadas aqui à medida que o conteúdo for apresentado.
(Observação: os links dos livros disponibilizados acima partem de um servidor que, em princípio, oferece tais materiais legalmente. Se for comprovado que este não é o caso, os links serão retirados sem aviso prévio)
Textos suplementares:
- R. Bott, L. Tu, Differential Forms in Algebraic Topology. Springer-Verlag, 1995.
- R. W. R. Darling, Differential Forms and Connections. Cambridge University Press, 1994.
- J. J. Duistermaat, J. A. C. Kolk, Multidimensional Real Analysis I – Differentiation; II – Integration. Cambridge University Press, 2004.
- H. Flanders, Differential Forms with Applications to the Physical Sciences. Academic Press, 1963.
- N. J. Hicks, Notes on Differential Geometry. Van Nostrand Reinhold, 1971.
- J. E. Marsden, A. J. Tromba, Vector Calculus (5a. edição). W. H. Freeman & Co., 2003.
- L. Tu, An Introduction to Manifolds (2a. edição). Springer-Verlag, 2011.
Recomendações e material didático suplementar:
Faremos uso tácito de conceitos vistos na disciplina BCN0407 – Funções de Várias Variáveis. Recomendamos fortemente que o aluno com dificuldades nos tópicos dessa disciplina faça uma revisão destes, pois isto não será feito em aula exceto nos casos previstos no Roteiro.
Avaliação:
A avaliação será feita por meio de cinco (5) provas curtas, de 45 minutos de duração, a serem aplicadas com um interstício de cerca de duas semanas entre uma prova e outra (mais feriados). A resolução de cada prova será feita em sala de aula imediatamente após seu término, e o restante da aula retomará a discussão teórica.
- Datas das provas:
P1 – 28.2 (sexta-feira);
P2 – 20.3 (sexta-feira – data alterada!);
P3 – 27.3 (sexta-feira);
P4 – 17.4 (sexta-feira);
P5 – 7.5 (quinta-feira);
Sub (se houver necessidade) – 8.5 (sexta-feira);
Rec – 14.5 (quinta-feira).
- Média preliminar (antes da prova de recuperação):
Mp = (P1 + P2 + P3 + P4 + P5)/5.
- Média final (após a prova de recuperação):
Mf = 0,6Rec + 0,4Mp.
- Critério de conceito final Cf (resp. conceito preliminar Cp) em função da média final Mf (resp. média preliminar Mp):
F – Mf (resp. Mp) < 4,5,
D – Mf (resp. Mp) = 4,5-5,2,
C – Mf (resp. Mp) = 5,3-6,9,
B – Mf (resp. Mp) = 7,0-8,4,
A – Mf (resp. Mp) = 8,5-10,0.
- A prova substitutiva será aplicada no final do quadrimestre e só poderá ser feita por alunos que não puderem comparecer a uma ou mais provas, com justificativa formal por escrito da ausência em cada prova perdida apresentada ao docente no máximo até o horário de início da prova substitutiva. Se o original da(s) justificativa(s) não puder ser entregue(s), ele deve ser pelo menos apresentado presencialmente para conferência e uma cópia escaneada enviada por email.
- Em virtude do método de avaliação adotado, cada prova substitutiva cobrirá apenas o conteúdo da(s) prova(s) perdida(s) pelo respectivo aluno.
- A prova de recuperação será única, cobrirá o conteúdo do quadrimestre inteiro e deverá ser aplicada pelo menos 72 horas após a divulgação dos conceitos finais, calculados após a aplicação da prova substitutiva (se houver necessidade de aplicar a última). Apenas alunos que ficaram com conceitos preliminares D e F (ver critério acima) após a aplicação da prova substitutiva poderão fazer essa prova.
- Haverá 15 minutos de tolerância para que o aluno que optar por fazer a prova de recuperação desista de fazê-lo e assim evitar que a nota da prova de recuperação entre na média final segundo o critério acima.
- Como as datas da P2, da Sub e da Rec são respectivamente destinadas à reposição dos feriados de 26.2 (Quarta-feira de Cinzas), 8.4 (aniversário de Santo André) e 1.5 (Dia do Trabalho), essas provas seguirão os horários e locais das aulas do dia da semana em que tenha caído o respectivo feriado sendo reposto. Ver calendário de reposição de feriados para mais detalhes.
- Quartas-feiras, 13h00-15h00, sala A-S305-3;
- Quintas-feiras, 17h00-19h00, sala A-S301-3;
- Sextas-feiras, 13h00-14h00, sala A-S309-1.
- Revisão de Álgebra Linear em
 : vetores, (sub)espaços vetoriais, dependência linear e bases. Matrizes e transformações lineares. Produto escalar, norma e distância euclideanas, lema de Riesz. Determinantes, multivetores e formas de volume orientadas associadas a uma base. Produto exterior. Mudanças de base e seu efeito sobre multivetores e formas de volume. Operador de Hodge sobre formas de volume, produto vetorial.
: vetores, (sub)espaços vetoriais, dependência linear e bases. Matrizes e transformações lineares. Produto escalar, norma e distância euclideanas, lema de Riesz. Determinantes, multivetores e formas de volume orientadas associadas a uma base. Produto exterior. Mudanças de base e seu efeito sobre multivetores e formas de volume. Operador de Hodge sobre formas de volume, produto vetorial. - Análise vetorial: aplicações diferenciáveis e campos vetoriais, operadores gradiente, divergente, rotacional (em
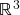 ) e laplaciano. Interpretação geométrica do gradiente. Formas diferenciais, derivada exterior e coderivada exterior. Operadores gradiente, divergente, rotacional e laplaciano revisitados.
) e laplaciano. Interpretação geométrica do gradiente. Formas diferenciais, derivada exterior e coderivada exterior. Operadores gradiente, divergente, rotacional e laplaciano revisitados. - Curvas, superfícies e subvariedades: caso parametrizado, cartas locais e descrição implícita, espaços tangentes / normais e campos vetoriais tangentes / normais. Parametrizações especiais: coordenadas polares, cilíndricas e esféricas.
- Integrais de caminho, de superfície e em subvariedades. Caso parametrizado, mudança de variáveis e partições de unidade. (Ou: por que precisamos de formas de volume?)
- Teorema Fundamental do Cálculo em várias variáveis: o teorema geral de Stokes. Casos particulares em duas e três dimensões: teoremas de Green, Gauss e Stokes clássico. Interpretação geométrica do divergente e do rotacional: fluxo e circulação de campos vetoriais. Interpretação geométrica do laplaciano: potencial de Newton e decomposição de Helmholtz de campos vetoriais em
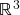 .
. - Tópicos suplementares (se houver tempo): derivada covariante em subvariedades, geodésicas e curvatura, campos tensoriais. Aplicações em Física: fluidos, Eletromagnetismo e Relatividade.
Listas de exercícios:
É extremamente importante que os alunos façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!
Os alunos que assim desejarem poderão entregar as suas resoluções das listas correspondentes à matéria de cada prova até o dia da prova correspondente. Tais listas serão avaliadas nos casos de média final limítrofe para aprovação (ver tabela de conversão de conceitos acima), convertendo-se num bônus de até 1,0 ponto na média final.
Monitoria, atendimento online e plantão de dúvidas:
Horários e locais de monitoria presencial (monitor Victor Guedes – a partir de quinta-feira, 20.2):
Atendimento online (Moodle): o Moodle servirá como plataforma online para envio e atendimento de dúvidas pelos monitores e/ou docentes da disciplina. Para mais informações, ver a página de monitoria de CVT do Gradmat.
Haverá um plantão de dúvidas às quartas-feiras das 16h30 às 18h00 e às quintas-feiras das 19h00 às 20h30, na minha sala (A-S543-2, Torre 2, Bloco A, campus Santo André). O plantão terá início no dia 13.2.
Roteiro:
Seguiremos de maneira aproximada o cronograma sugerido para o curso de CVT pelo Gradmat, com as seguintes modificações:

