Teorema do Núcleo e da Imagem (prova). Determinantes, formas de volume e
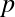 -formas
-formas
Vídeo
Teorema do Núcleo e da Imagem
Recapitularemos em breve o contexto da aula 9. Sejam ![]() espaços vetoriais (reais), e
espaços vetoriais (reais), e ![]() uma transformação linear (t.l.) de
uma transformação linear (t.l.) de ![]() em
em ![]() , ou seja, dados vetores
, ou seja, dados vetores ![]() em
em ![]() e um escalar
e um escalar ![]() quaisquer, temos que
quaisquer, temos que
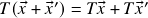 ;
;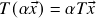 ,
,
(lembrar que escrevemos ![]() se
se ![]() é uma t.l.) de modo que se
é uma t.l.) de modo que se ![]() é uma combinação linear (c.l.) de vetores
é uma combinação linear (c.l.) de vetores ![]() com coeficientes
com coeficientes ![]() ,
, ![]() , então
, então
![Rendered by QuickLaTeX.com \[T\left(\sum^k_{j=1}\alpha_j\vx_j\right)=\sum^k_{j=1}\alpha_j T\vx_j\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-45fa8725121c048aae74dffd2fbf38f1_l3.png)
![]()
e a imagem inversa de ![]() por
por ![]()
![]()
Em particular, se ![]() , escrevemos
, escrevemos ![]() .
.
Cabe aqui uma observação sobre a notação empregada: notar que ![]() não precisa ser invertível para definirmos imagens inversas, pois
não precisa ser invertível para definirmos imagens inversas, pois ![]() e, em particular,
e, em particular, ![]() denotam subconjuntos de
denotam subconjuntos de ![]() , não vetores. Assim,
, não vetores. Assim, ![]() pode ser vazio (nesse caso,
pode ser vazio (nesse caso, ![]() não pode ser sobrejetora) ou ter mais de um vetor (nesse caso,
não pode ser sobrejetora) ou ter mais de um vetor (nesse caso, ![]() não pode ser injetora). Somente no caso em que
não pode ser injetora). Somente no caso em que ![]() é bijetora (i.e. iinvertível) é que
é bijetora (i.e. iinvertível) é que ![]() é unitário para todo
é unitário para todo ![]() e portanto pode ser identificado com seu único elemento, definindo assim a inversa
e portanto pode ser identificado com seu único elemento, definindo assim a inversa ![]() de
de ![]() .
.
Segue dessas definições que
![Rendered by QuickLaTeX.com \[\begin{split} T(L(S)) &=\left\{\vy=T\left(\sum^k_{j=1}\alpha_j\vx_j\right)\ \bigg|\ \alpha_1,\ldots,\alpha_k\in\RR\ ,\, \vx_1,\ldots,\vx_j\in S\right\}\\ &=\left\{\vy=\sum^k_{j=1}\alpha_jT\vx_j\ \bigg|\ \alpha_1,\ldots,\alpha_k\in\RR\ ,\,\vx_1,\ldots,\vx_j\in S\right\}\\ &=L(T(S)) \end{split}\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-ac3f634ba9721c3d0ae06b48e56297dd_l3.png)
— em particular, a imagem
![]()
de ![]() é subespaço vetorial de
é subespaço vetorial de ![]() – e que o núcleo
– e que o núcleo
![]()
de ![]() é subespaço vetorial de
é subespaço vetorial de ![]() : se
: se ![]() e
e ![]() quaisquer, então
quaisquer, então
![]()
e
![]()
portanto ![]() .
.
Por definição, ![]() é sobrejetora se e somente se
é sobrejetora se e somente se
![]()
Além disso, ![]() é injetora se e somente se
é injetora se e somente se
![]()
De fato, se ![]() e
e ![]() satisfazem
satisfazem ![]() , temos que
, temos que ![]() e portanto
e portanto ![]() . Conversamente, temos que se
. Conversamente, temos que se ![]() então
então ![]() para todo
para todo ![]() . Logo, se
. Logo, se ![]() é injetora, nesse caso
é injetora, nesse caso ![]() . A sobrejetividade e a injetividade de uma t.l.
. A sobrejetividade e a injetividade de uma t.l. ![]() podem ser expressas em termos de sua ação sobre (certos) subconjuntos l.i.
podem ser expressas em termos de sua ação sobre (certos) subconjuntos l.i. ![]() :
:
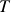 é sobrejetora se e somente se, dada uma base
é sobrejetora se e somente se, dada uma base 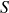 qualquer de
qualquer de 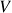 , temos que
, temos que 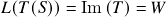 . (a primeira identidade segue do cálculo acima, e a segunda identidade é a definição da sobrejetividade de
. (a primeira identidade segue do cálculo acima, e a segunda identidade é a definição da sobrejetividade de 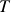 )
)-
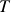 é injetora se e somente se, dado um subconjunto l.i.
é injetora se e somente se, dado um subconjunto l.i. 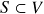 qualquer, temos que
qualquer, temos que 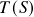 \emph{também é l.i.}. (suponha que
\emph{também é l.i.}. (suponha que 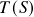 é l.i. para todo
é l.i. para todo 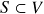 l.i., então
l.i., então 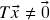 se
se 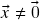 e portanto
e portanto 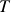 é injetora. Conversamente, se
é injetora. Conversamente, se 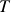 é injetora e
é injetora e  são l.i., sejam
são l.i., sejam 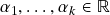 tais que
tais que 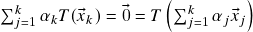 . Então
. Então 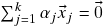 e portanto
e portanto 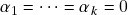 , logo
, logo  são l.i.)
são l.i.)
Em particular, ![]() é bijetora se e somente se
é bijetora se e somente se ![]() é base de
é base de ![]() para toda base
para toda base ![]() de
de ![]() . Em outras palavras, o exemplo típico de t.l.’s bijetoras ocorre ao efetuarmos uma mudança de base. Se
. Em outras palavras, o exemplo típico de t.l.’s bijetoras ocorre ao efetuarmos uma mudança de base. Se ![]() tem dimensão finita, ambos os fatos acima são casos particulares de um resultado geral, conhecido como Teorema do Núcleo e da Imagem. Dados espaços vetoriais (reais)
tem dimensão finita, ambos os fatos acima são casos particulares de um resultado geral, conhecido como Teorema do Núcleo e da Imagem. Dados espaços vetoriais (reais) ![]() e
e ![]() , o posto (“rank” em inglês)
, o posto (“rank” em inglês) ![]() de
de ![]() é dado por
é dado por
![]()
e a nulidade ![]() de
de ![]() por
por
![]()
Obviamente ![]() pois
pois ![]() se
se ![]() é base de
é base de ![]() e
e ![]() é subespaço vetorial de
é subespaço vetorial de ![]() .
.
Teorema do Núcleo e da Imagem. Sejam
espaços vetoriais (reais),
, e
. Então
Prova. Definamos
,
. Sejam
uma base de
e
uma base de
, de modo que
para algum
,
. Obviamente
para todo
; mostraremos agora que definindo
, temos que
é base de
. Primeiramente, notar que
é l.i.: dados
tais que
, temos que
e portanto
pois
é l.i.. Logo,
e portanto
pois
é l.i.. Falta apenas concluir que
— para tal, notar que dado
, podemos escrever
para uma (única) escolha de
. Defina
Segue que
e portanto
, pois
logo podemos escrever
para uma (única) escolha de
e portanto
, como desejado.
O Teorema do Núcleo e da Imagem possui várias consequências. No que se segue, ![]() são espaços vetoriais (reais) com
são espaços vetoriais (reais) com ![]() .
.
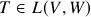 é sobrejetora se e somente se
é sobrejetora se e somente se 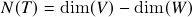 . Em particular,
. Em particular, 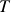 não pode ser sobrejetora se
não pode ser sobrejetora se 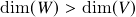 .
.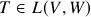 é injetora se e somente se
é injetora se e somente se 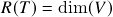 .
.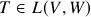 é bijetora se e somente se
é bijetora se e somente se 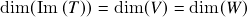 .
.- Se
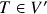 , então
, então 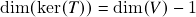 ou
ou 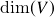 , e o último caso ocorre se e somente se
, e o último caso ocorre se e somente se  .
.
O fato (iv) acima fornece uma maneira alternativa de obter o Lema de Riesz:
Lema de Riesz. Seja
um espaço vetorial (real),
. Dado
, existe um único vetor
tal que
para todo
– a saber,
onde
é um vetor ortogonal a
(notar que, pelo Teorema do Núcleo e da Imagem,
é único a menos de um múltiplo escalar).
Prova. Comecemos com a questão da unicidade. Se
são tais que
para todo
, então
para todo
. Em particular, tomando
obtemos
e portanto
. Passando agora à questão da existência, se
obviamente não há outra escolha para
a não ser
. Se
, seja
tal que
. Podemos então construir uma base o.n.
de
e portanto a projeção ortogonal
sobre
. De maneira similar à adotada na ortonormalização de Gram-Schmidt, defina
de modo que
é base o.n. de
. Mostraremos agora que se
tem as propriedades listadas no enunciado do Lema de Riesz, então
De fato, dado
qualquer, podemos escrever
e portanto
como desejado.
Notar que ![]() e
e ![]() para
para ![]() ,
, ![]() quaisquer. Vamos agora estabelecer a relação da fórmula obtida no Lema de Riesz com a fórmula que já tínhamos obtido anteriormente: se
quaisquer. Vamos agora estabelecer a relação da fórmula obtida no Lema de Riesz com a fórmula que já tínhamos obtido anteriormente: se ![]() e
e ![]() é uma base o.n. de
é uma base o.n. de ![]() , então
, então
![Rendered by QuickLaTeX.com \[ \begin{split} V\ni\vx &=\sum^n_{j=1}x_j\ve_j\ \Then\ T\vx=\sum^n_{j=1}x_j T\ve_j=\spr{\vx_T,\vx}\\ \Then\ \vx_T &=\sum^n_{j=1}(T\ve_j)\ve_j\ . \end{split} \]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-25ce870fac213fa887722fd3dc84765b_l3.png)
Em particular, ![]() é ortogonal a
é ortogonal a ![]() e
e
![Rendered by QuickLaTeX.com \[ T\vx_T=\sum^n_{j=1}(T\ve_j)^2=\|\vx_T\|^2\ , \]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-321c5d51be6c8fd78d3291ab3e4db454_l3.png)
Aproveitamos o momento para introduzir uma notação alternativa para ![]() , que será a notação padrão daqui em diante. Dados
, que será a notação padrão daqui em diante. Dados ![]() ,
, ![]() , definimos
, definimos ![]() ,
, ![]() como
como
![]()
Fica claro que ![]() e
e ![]() para
para ![]() ,
, ![]() quaisquer. Além disso, as aplicações
quaisquer. Além disso, as aplicações ![]() e
e ![]() são t.l.’s (exercício: verifique!), portanto denotar-las-emos por isomorfismos musicais.
são t.l.’s (exercício: verifique!), portanto denotar-las-emos por isomorfismos musicais.
Próxima aula
Na próxima aula começaremos a falar de determinantes, formas de volume e ![]() -formas, partindo da motivação dada pela área de paralelogramos.
-formas, partindo da motivação dada pela área de paralelogramos.

![Rendered by QuickLaTeX.com \[T\left(\sum^{k+l}_{j=1}\alpha_j\ve_j\right)=\og=\sum^{k+l}_{j=1}\alpha_jT\ve_j=\sum^l_{i=1}\alpha_{k+i}\vf_i\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-14a1072052e770b63d82426c14746a99_l3.png)
![Rendered by QuickLaTeX.com \[T\vx=\sum^l_{i=1}x_{k+i}\vf_i=\sum^l_{i=1}x_{k+i} T\ve_{k+i}=T\left(\sum^l_{i=1}x_{k+i}\ve_{k+i}\right)\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-5aec1196327d3d89502af227ba3d4df6_l3.png)
![Rendered by QuickLaTeX.com \[\vx_1=\sum^l_{i=1}x_{k+i}\ve_{k+i}\ ,\,\vx_0=\vx-\vx_1\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-b60e9f6cb56d55def974c6a39d6cbc7e_l3.png)
![Rendered by QuickLaTeX.com \[T\vx_1=\sum^l_{i=1}x_{k+i}\vf_1=T\vx\ ,\,T\vx_0=T(\vx-\vx_1)=T\vx-T\vx=\og\ ,\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-658cbb4bde6e183ad48164d4b8a43730_l3.png)
![Rendered by QuickLaTeX.com \[\vx_T=\begin{cases} \og & (T=0) \\ \frac{T\vz_T}{\|\vz_T\|^2}\vz_T &(T\neq 0) \end{cases}\ ,\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-e1f50192287183fb56381646fa3eadb4_l3.png)
One Comment