MCTB010 – 1q’20 – Aula 1 (12.2.20)

Motivação e objetivos

Como seu próprio nome diz, o Cálculo em Várias Variáveis lida com as operações de derivação e integração sobre funções de várias variáveis. Isso é feito inicialmente tratando-se cada variável da função separadamente enquanto as demais variáveis são mantidas fixas, de modo a sermos capazes de usar conhecimento prévio de Cálculo de funções de uma variável. No caso da derivada, esse procedimento nos leva à noção de derivadas parciais e, mais em geral, à noção de derivadas direcionais. No caso de integrais, contudo, queremos ser capazes de integrar em domínios que, intuitivamente, tem dimensão mais alta, mas a ideia subjacente à construção da integral de Riemann é facilmente generalizável a tais domínios — mais precisamente, passamos a calcular volumes ao invés de áreas. Além disso, dentro de certas condições (estabelecidas e.g. por alguma versão do teorema de Fubini), a integral de Riemann em várias variáveis pode ser calculada calculando-se a integral em cada uma das variáveis separadamente e em sucessão: a chamda integral iterada.

O ingrediente que falta nisto tudo é justamente a conexão entre derivação e integração para várias variáveis. No caso de funções de uma variável, tal conexão é estabelecida pelo Teorema Fundamental do Cálculo. Obviamente, podemos aplicar esse teorema separadamente em cada variável, mas seu significado geométrico não é claro de um ponto de vista de várias variáveis pois é vinculado a uma escolha arbitrária de variável. Para elucidar essa afirmação, atentemos por ora ao (segundo) Teorema Fundamental do Cálculo para funções de uma variável, que nos diz que se $f:[a,b]\To\RR$ é derivável em $[a,b]$ e sua derivada $f'$ é contínua em $[a,b]$ , então

(1) $\begin{equation*} f(b)-f(a)=\int^b_a f'(t)dt\ . \end{equation*}$

A busca por uma extensão genuína dessa fórmula para uma função de $n>1$ variáveis $f:U\To\RR$ , onde $U\subset\RR^n$ , envolve as seguintes questões:

O lado esquerdo de (1) envolve todos os valores de $f$ na fronteira do seu domínio. Qual o seu significado em dimensões mais altas?
O lado direito de (1) envolve a integral de 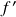$f'$ sobre o domínio. Qual a noção de derivada que devemos usar dentro da integral em dimensões mais altas para obtenhamos igualdade com o lado esquerdo? Claramente não pode ser nenhuma derivada parcial ou mesmo direcional de $f$ , pois nesse caso o Teorema Fundamental do Cálculo em uma variável essencialmente nos diz que estamos integrando sobre apenas uma das variáveis, cuja escolha é arbitrária e claramente leva a resultados diferentes no lado esquerdo para cada variável.

Para buscarmos respostas a essas perguntas, é pertinente neste momento nos perguntarmos qual seria o uso de um “Teorema Fundamental do Cálculo para várias variáveis”. No caso de funções de uma variável, podemos citar por exemplo a aplicação original dada por Newton ao estudo do movimento dos corpos (pontuais): a partir da velocidade $v(t)=x'(t)$ de uma trajetória unidimensional $x(t)$ de uma partícula pontual ao longo de um intervalo de tempo $t\in[a,b]$ , podemos obter o seu deslocamento total $x(b)-x(a)$ integrando $v(t)$ em $[a,b]$ .

Um análogo multidimensional dessa situação pode ser encontrado na descrição do movimento de fluidos. Podemos pensar num fluido num domínio (digamos) tridimensional $U\subset\RR^3$ (que pode representar um recipiente, um lago, etc.) como um contínuo de inúmeras partículas constituintes em movimento dentro de $U$ . Imaginemos, numa situação ideal, que pudéssemos “colorir” uma dessas partículas na posição $\vx=(x,y,z)\in U$ num instante $t_0$ e seguir seu movimento ao longo do tempo. Isso nos permitiria traçar a trajetória

$\vx(t)=(x(t),y(t),z(t))$

dessa partícula em função do tempo $t$ e, em particular, calcular sua velocidade

$\vv(t_0)=\vx'(t_0)=(x'(t_0),y'(t_0),z'(t_0))$

no instante $t_0$ . Se fizermos isso com todas as partículas do fluido em $U$ no instante $t_0$ , o resultado é uma regra que atribui a cada $\vx\in U$ o vetor velocidade $\vV_{t_0}(\vx)=\vv(t_0)$ da partícula do fluido no instante $t_0$ que, nesse instante, passa pela posição $\vx=\vx(t_0)$ . A aplicação $\vV_{t_0}:U\To\RR^3$ obtida dessa forma é uma “fotografia” do movimento do fluido como um todo no instante $t_0$ – um campo vetorial (tridimensional) em $U$ , que neste caso chamamos de campo de velocidades do fluido em $U$ no instante $t_0$ . Obviamente, podemos fazer o mesmo em qualquer outro instante de tempo $t$ e obter o campo de velocidades do fluido $\vV_t(\vx)$ nesse instante, resultando num campo vetorial tridimensional $\vV:\RR\times U\To\RR^3$ dado por $\vV(t,\vx)=\vV_t(\vx)$ . Em particular, o domínio e o contradomínio de campos vetoriais não precisam ter a mesma dimensão.

Agora podemos tentar descobrir qual seria o análogo para várias variáveis dos objetos envolvidos nos dois lados da fórmula (1). No caso, consideremos apenas as variáveis espaciais $\vx=(x,y,z)$ e o campo de velocidades $\vV_t(\vx)$ em $U$ no instante (digamos) $t$ . Seja um subdomínio $K\subset U$ com fronteira $\partial K$ e interior não-vazio, que será nosso domínio de integração.

Um análogo possível para o lado esquerdo de (1) é o fluxo do fluido através de $K$ no instante $t$ , que intuitivamente é a taxa de variação de quantidade de fluido que atravessa $\partial K$ nesse instante. No caso unidimensional, vemos que um fluxo positivo através de cada ponto de $K=[a,b]$ significa fluido saindo de $K$ , por isso $f(b)$ contribui com sinal positivo e $f(a)$ , com sinal negativo. No caso multidimensional a situação é mais complicada, pois a quantidade de fluido que entra ou sai através de cada ponto de $\partial K$ depende do ângulo que a velocidade do fluido faz com o vetor normal a $\partial K$ nesse ponto. Isso é mais um indicativo de que um análogo razoável do Teorema Fundamental do Cálculo em várias variáveis necessariamente envolve campos vetoriais – a informação direcional de $\vV_t$ é essencial na definição de fluxo.

Finalmente, como devemos “somar” a contribuição de cada ponto de $\partial K$ para o fluxo do fluido, concluímos que uma integral sobre $\partial K$ está envolvida na definição de fluxo. Quanto ao lado direito de (1), intuitivamente devemos ter a integral de algum tipo de “derivada” de $\vV_t$ sobre $K$ . A ideia que emerge é que integrar tal “derivada” num domínio $n$ -dimensional equivale a integrar na fronteira desse domínio, que possui “uma dimensão a menos”. Isso é exatamente o que ocorre no caso unidimensional. Assim, já vislumbramos a simplificação calculacional que esperamos obter com um Teorema Fundamental do Cálculo, bem como qual seria a relação conceitual dessa “derivada” com o processo de integração em várias variáveis.

Obviamente, o domínio $K$ deve ser tal que faça sentido calcular integrais tanto em $K$ como em $\partial K$ . Contudo, a noção de derivada de campos vetoriais que entra no que seria a versão de várias variáveis do Teorema Fundamental do Cálculo ainda nos elude com as informações que temos. Para encontrar essa noção, precisamos reconsiderar a construção de integrais múltiplas e a própria noção de volume de um ponto de vista mais geométrico. A motivação para tal tarefa agora é evidente: como visto acima, um teorema desse tipo nos permite igualar o fluxo de um campo vetorial em $\partial K$ à integral em $K$ de uma certa “derivada” desse campo. No caso de um fluido, a dinâmica desse campo de velocidade segue certas equações envolvendo derivadas parciais deste, que permitem relacionar essa “derivada” a outras quantidades envolvidas nessa dinâmica (fontes, sorvedouros, etc.). Desta forma, o Teorema Fundamental do Cálculo é uma ferramenta fundamental no estudo da dinâmica de fluidos.

Algo similar ocorre no estudo do Eletromagnetismo. Aqui, a situação é a seguinte: uma partícula de massa $m$ e dotada de carga elétrica movendo-se ao longo da trajetória $\vx(t)$ é sujeita em cada ponto $\vx(t)$ por onde passa a uma força $\vF(t,\vx(t))$ , de modo que tal trajetória está sujeita à Segunda Lei de Newton

$m\vx''(t)=\vF(t,\vx(t))\ .$

O campo de forças $\vF(t,\vx)$ é um campo vetorial tridimensional que, por sua vez, depende de dois outros campos $\vE(t,\vx)$ e $\vB(t,\vx)$ — respectivamente chamados de campo elétrico e campo magnético. Infelizmente, a imagem geométrica de $\vE$ e (particularmente) $\vB$ não é tão simples quando a do campo de velocidades de um fluido, mas as equações diferenciais que determinam sua dinâmica são consideravelmente mais simples (dentro do âmbito da Física Clássica). Novamente, podemos usar o Teorema Fundamental do Cálculo para relacionar a “derivada” de tais campos com as fontes destes (cargas e correntes elétricas) por meio das equações supracitadas.

Retomaremos as aplicações físicas mencionadas acima em posts subsequentes. Nossa tarefa principal, agora, é desenvolver as ferramentas necessárias para a formulação do Teorema Fundamental do Cálculo em várias variáveis.

MCTB010 – 1q’20 – Aula 1 (12.2.20)

Motivação e objetivos

Pedro Lauridsen Ribeiro

One Comment

Leave a Reply Cancel reply