
Este é o plano de ensino para a disciplina MCTB010 – Cálculo Vetorial e Tensorial (CVT) conforme ministrada no primeiro quadrimestre de 2020 para as seguintes turmas:
- A1 – Noturno, campus Santo André – horário presencial: 4as. feiras 19h00-21h00 e 6as. feiras 21h00-23h00.
- B1 – Noturno, campus Santo André – horário presencial: 4as. feiras 21h00-23h00 e 6as. feiras 19h00-21h00.
Aqui encontram-se informações específicas sobre as turmas acima no contexto dos Estudos Continuados Emergenciais (ECE). Em acordo com a Resolução no. 239/2020 do ConsEPE, este plano de ensino estará disponível também no ambiente virtual de aprendizagem (AVA) Moodle. As atividades da disciplina serão retomadas em 22.4.
Confira o comunicado de 6 de abril sobre o ECE.
Dúvidas a respeito de ECE? Veja os detalhes sobre o ECE: implementação e FAQ.
Novidades
Notícias recentes sobre o funcionamento do curso serão postadas aqui.
- (17.1.21) Nota atualizada sobre o período de avaliação presencial do ECE (reprodução do aviso divulgado pelo Moodle em 23.12.20).
- (24.7.20) Em resposta às várias consultas que tenho recebido sobre o período de avaliação presencial do ECE, venho informar que no momento a UFABC tem um grupo de trabalho estudando possíveis protocolos de retorno às atividades presenciais, mas até o presente momento não há previsão de agendamento do período de avaliação. Pretendo fazer atualizações periódicas de conteúdo nas próximas semanas para manter o contato com as turmas – em particular, os posts em blog das aulas (que acabaram ficando em segundo plano em virtude das dificuldades técnicas com o envio das aulas em vídeo), o completamento das notas de aula e a edição dos vídeos deverão ser feitos. Possivelmente algum material adicional será acrescentado visando dar subsídios para a Lista 4, cujo envio de resoluções também está previsto para o período de avaliação presencial.
- (24.7.20) As notas da P1 e das resoluções das Listas 1 a 3 deverão ser divulgadas até sexta-feira, 9.10.
- (13.7.20) O NTI e a Cetic alteraram o endereço do Moodle na UFABC para https://moodle-cetic.ufabc.edu.br como parte da transição para uma versão mais recente do Moodle a partir do próximo quadrimestre letivo que passará em breve a funcionar no endereço anterior. Esta disciplina por enquanto permanecerá na versão antiga, acessada pelo endereço acima.
- (3.7.20) As notas da P1 e das resoluções das Listas 1 a 3 estarão disponíveis até sábado, 25.7.
- (27.6.20) A aula 20 (29.5) está disponível em vídeo.
- (26.6.20) A aula 19 (27.5) está disponível em vídeo.
- (25.6.20) Infelizmente problemas técnicos impossibilitaram o envio das aulas em vídeo referentes ao material da Lista 4 em tempo hábil para tornar factível o envio de resoluções dessa Lista neste final de ECE. Assim, ao invés da Lista 4 serão cobrados mais exercícios da Lista 3 – mais especificamente, dentre os exercícios referentes ao conteúdo das aulas 18 e 19 (ver a a seção “Aulas”abaixo para os trechos correspondentes das notas de aula). O período de envio de resoluções será o mesmo – a partir da noite de sexta-feira, 26.6 as resoluções poderão ser enviadas até as 23h59 de segunda-feira, 29.6.
- (25.6.20) A Lista 4 será disponibilizada quando for possível, visando uma preparação futura para o período de avaliação presencial pós-ECE ainda a ser agendado pela UFABC.
- (25.6.20) Devido à priorização da disponibilização de conteúdo, as notas da P1 e das resoluções das Listas 1 a 3 serão disponibilizadas até sexta-feira, 3.7. O prazo para lançamento de conceitos foi estendido pela Prograd até 18.7, de modo que haverá tempo hábil para a vista das correções das resoluções das listas pelo Moodle.
- (25.6.20) As notas de aula foram atualizadas com correções, melhorias e o material até a aula 21.
- (24.6.20) A aula 18 (22.5) está disponível em vídeo. Os posts em blog a partir da aula 11 serão feitos posteriormente, o material das aulas está disponível em forma escrita nas notas de aula.
- (22.6.20) Haverá um plantão de dúvidas adicional na sexta-feira, 26.6 no horário usual (19h00-21h00).
- (22.6.20) O período de envio das resoluções da Lista 4 será postergado para dar mais tempo aos alunos assimilarem o material dessa lista. Assim, o período para envio de resoluções da Lista 4 será aberto na noite de sexta-feira, 26.6, que poderão ser enviadas até as 23h59 de segunda-feira, 29.6.
- (19.6.20) A Lista 4 será disponibilizada até quinta-feira, 25.6.
- (15.6.20) Para garantir tempo hábil para a assimilação do conteúdo restante do curso, haverá um novo ajuste no calendário de entrega das resoluções das listas. Haverá novamente apenas quatro (4) listas de exercícios, com a Lista 4 condensando o conteúdo das antigas Listas 4 e 5. O período de envio de resoluções da Lista 4 será o mesmo da lista 5. Ou seja, o período de envio das resoluções da Lista 4 será aberto na noite de terça-feira, 23.6, que poderão ser enviadas até as 23h59 de sexta-feira, 26.6.
- (5.6.20) Devido às dificuldades técnicas com o envio e disponibilização dos vídeos das aulas, o período de envio das resoluções da Lista 3 será adiado novamente. Haverá abertura do Moodle para envio das resoluções na noite de terça-feira, 9.6, que poderão ser enviadas até as 23h59 de sexta-feira, 12.6. Peço desculpas pelo transtorno.
- (5.6.20) O plantão de dúvidas de sexta-feira, 12.6 será remarcado para segunda-feira, 22.6 no mesmo horário (19h00-21h00).
- (1.6.20) A reposição do plantão de dúvidas de 22.5, originalmente marcada para hoje (segunda-feira, 1.6), será remarcada para segunda-feira, 15.6, no mesmo horário (19h00-21h00).
- (29.5.20) As notas da P1 e das resoluções das Listas 1 e 2 estarão disponíveis até sábado, 3.7.
- (29.5.20) Conforme disposto no Ato Decisório no. 188/2020 do ConsEPE, de 28 de maio de 2020, foi decidido que o período de atividades remotas dos Estudos Continuados Emergenciais (ECE), originalmente previsto na Resolução no. 239/2020 do ConsEPE para se encerrar no sábado, 6.6, será prorrogado por mais três semanas e deverá agora se encerrar no sábado, 27.6. Para mais detalhes, consultar a página atualizada de informações sobre o ECE. Em vista disso, das dificuldades técnicas enfrentadas na disponibilização do conteúdo das aulas, e das consequências dos atrasos decorrentes dessas dificuldades para a assimilação desse conteúdo pelos alunos em tempo hábil e para o cumprimento da ementa da disciplina, decidi fazer uso completo desse período de extensão. Isso acarretará as mudanças no cronograma do curso listadas a seguir. Observo que, em respeito ao disposto na Resolução no. 239/2020 e no Ato Decisório no. 188/2020 do ConsEPE, a prova presencial originalmente prevista após o término do ECE e a reabertura dos campi da UFABC a atividades presenciais está mantida.
- (29.5.20) O período de envio das resoluções da Lista 3 será adiado. Haverá abertura do Moodle para envio das resoluções, na noite de sexta-feira, 5.6, que poderão ser enviadas até as 23h59 de segunda-feira, 8.6.
- (29.5.20) O período de envio das resoluções da Lista 4 será adiado. Haverá abertura do Moodle para envio das resoluções na noite de segunda-feira, 15.6, que poderão ser enviadas até as 23h59 de quinta-feira, 18.6.
- (29.5.20) A Lista 5 será resgatada. Haverá abertura do Moodle para envio das resoluções na noite de terça-feira, 23.6, que poderão ser enviadas até as 23h59 de sexta-feira, 26.6.
- (29.5.20) Haverá cinco (5) aulas adicionais (aulas 23 a 27), visando o completamento da ementa.
- (29.5.20) Os plantões de dúvidas às quartas-feiras e sextas-feiras das 19h00 às 21h00 serão prorrogados até quarta-feira, 24.6.
- (28.5.20) A aula 17 (20.5) está disponível em vídeo e estará disponível no blog até quinta-feira, 11.6.
- (26.5.20) A aula 16 (15.5) está disponível em vídeo e estará disponível no blog até quinta-feira, 11.6.
- (25.5.20) Devido a dificuldades técnicas com o envio dos vídeos das aulas e o consequente atraso na disponibilização das últimas, haverá um novo ajuste no calendário de entrega das resoluções das listas. Haverá apenas quatro (4) listas de exercícios, com a Lista 4 condensando o conteúdo das antigas Listas 4 e 5, e o período de envio das resoluções da Lista 3 será adiado mais uma vez. Haverá abertura do Moodle para envio das resoluções da Lista 3 na noite de sábado, 30.5, que poderão ser enviadas até as 23h59 de terça-feira, 2.6, e haverá abertura do Moodle para envio das resoluções da Lista 4 na noite de sexta-feira, 5.6, que poderão ser enviadas até as 23h59 de segunda-feira, 8.6.
- (22.5.20) A aula 15 (13.5) está disponível em vídeo e estará disponível no blog até quinta-feira, 11.6.
- (20.5.20) A aula 14 (8.5) está disponível em vídeo e estará disponível no blog até quinta-feira, 11.6.
- (20.3.20) Devido à antecipação do feriado de Corpus Christi para sexta-feira, 22.5, não haverá plantão de dúvidas por videoconferência nessa data. Pelo mesmo motivo, o calendário de entrega das resoluções das Listas 3 e 4 será alterado da seguinte maneira: haverá abertura do Moodle para envio das resoluções da Lista 3 na noite de segunda-feira, 25.5, que poderão ser enviadas até as 23h59 de quinta-feira, 28.5, e haverá abertura do Moodle para envio das resoluções da Lista 4 na noite de sábado, 30.5, que poderão ser enviadas até as 23h59 de terça-feira, 2.6. O calendário de entrega de resoluções da Lista 5 está mantido. O plantão de dúvidas de 22.5 será reposto na segunda-feira, 1.6, no mesmo horário (19h00-21h00).
- (18.5.20) A Lista 3 está disponível.
- (15.5.20) Os posts em blog das aulas 11 a 17 estarão online até quinta-feira, 11.6.
- (15.5.20) a Lista 3 estará disponível até segunda-feira, 18.5.
- (15.5.20) As permissões para alunos das minhas turmas postarem dúvidas no fórum do Moodle foram corrigidas.
- (14.5.20) As notas de aula foram atualizadas. A Subseção I.3.2 foi revisada e foi adicionada a Seção A.1 do Apêndice A.
- (11.5.20) O monitor Victor Guedes começou a fazer atendimento de dúvidas da disciplina de CVT por videoconferência síncrona às sextas-feiras das 13h00 às 14h00. Consulte esta página para mais detalhes.
- (10.5.20) A aula 13 (6.5) está disponível em vídeo e estará disponível no blog até terça-feira, 19.5.
- (9.5.20) A aula 12 (29.4) está disponível em vídeo e estará disponível no blog até terça-feira, 19.5.
- (8.5.20) A seleção dos exercícios da Lista 1 a serem entregues pelo Moodle será disponibilizada entre 21h00 e 22h00 de hoje.
- (8.5.20) As notas de aula foram atualizadas. Agora o Capítulo I completo está disponível (sujeito a revisões).
- (5.5.20) Ainda sobre o envio das resoluções das listas de exercícios – notar que a Lista 1 também terá uma seleção de exercícios a serem enviados para avaliação pelo Moodle, apesar de ter sido dada a opção da entrega da resolução da Lista 1 logo após a Prova 1 no período pré-ECE. A razão é a seguinte: o objetivo das listas com resolução entregue no período pré-ECE era contarem como um bônus na média final (após a aplicação da prova de recuperação) nos casos limítrofes para aprovação. Assim, as resoluções da Lista 1 entregues nesse período ainda contarão segundo esse critério – como apenas uma das cinco listas pôde ser entregue antes da vigência do ECE, o bônus na média final deverá ser de até 0,2 pontos ( = 20% do bônus de até 1,0 ponto originalmente correspondente às cinco listas). Os alunos que entregaram a sua resolução da Lista 1 poderão enviar a resolução dos exercícios selecionados dessa Lista pelo Moodle normalmente.
- (5.5.20) Detalhes sobre o envio das resoluções das listas de exercícios – como comunicado anteriormente neste plano de ensino (ver seção “Avaliação” abaixo), as resoluções deverão ser enviadas por um canal do Moodle a ser disponibilizado para cada lista – não serão aceitas outras formas de envio. Uma seleção dos exercícios de cada lista a serem resolvidos será divulgada por um aviso através do Moodle juntamente com o procedimento para envio. Logo a partir dessa divulgação, haverá um prazo de três dias para o envio das resoluções, a ser estipulado para cada lista. Após o término do prazo para uma determinada lista, não serão mais aceitos envios de resoluções para esta. O calendário de divulgações das seleções de exercícios a serem resolvidos para cada lista pode ser encontrado na seção “Avaliação” abaixo.
- (30.4.20) Em virtude do feriado de sexta-feira, 1.5, não haverá plantão de dúvidas ou aula nesse dia.
- (30.4.20) As notas de aula foram atualizadas com o material até a aula 12 (e um pouco além). O post em blog da aula 11, bem como o vídeo e o post em blog das aulas 12 e 13, estarão disponíveis até quarta-feira, 13.5.
- (29.4.20) A Lista 2 está disponível. Por favor, comunicar quaisquer erros ou imprecisões encontrados nos enunciados ou no gabarito parcial.
- (26.4.20) A aula 11 (24.4) está disponível em vídeo e estará disponível no blog até quarta-feira, 13.5.
- (26.4.20) A aula 10 (22.4) está disponível em vídeo.
- (24.4.20) Devido a dificuldades técnicas com a largura de banda da internet para envio de arquivos, o envio dos vídeos das aulas 10 e 11 deverão ser concluídos até segunda-feira, 27.4.
- (23.4.20) A aula 10 (22.4) está disponível no blog e estará disponível em vídeo em breve. As notas de aula serão atualizadas com o material das aulas 10 e 11 até terça-feira, 28.4.
- (22.4.20) A aula 10 (22.4) estará disponível em vídeo e no blog até amanhã (quinta-feira, 23.4).
- (22.4.20) A aula 2 (14.2) já está disponível no blog.
- (21.4.20) As aulas 1 a 9, ministradas presencialmente no período pré-ECE (12.2 a 13.3), serão gradativamente transpostas para o formato de blog para facilitar a recapitulação do conteúdo previamente apresentado no curso, bem como a solução de dúvidas decorrentes desse processo. A aula 1 (12.2) já está disponível no blog.
- (6.4.20) A Lista 2 será disponibilizada até quarta-feira, 29.4.
- (6.4.20) As notas da P1 serão divulgadas até sexta-feira, 8.5.
Aulas
Os links para o material de cada aula (vídeo e blog), acompanhados de uma breve descrição desta, serão listados aqui.
- Aula 20 – 3.6 (vídeo, blog – Subseções II.1.1 e II.1.2, pp. 121-132 das notas de aula): Campos escalares e campos vetoriais – definição, operações vetoriais pontuais e sua diferenciabilidade. Campos de transformações lineares. Operadores diferenciais lineares de ordem 1 – definição e composição. Exemplos de operadores diferenciais lineares de ordem 1: derivadas parciais, diferencial, gradiente, derivada ao longo de um campo vetorial, divergente e rotacional. O laplaciano como exemplo de operador diferencial linear de ordem 2.
- Aula 19 – 29.5 (vídeo, blog – Subseções I.3.3 e I.3.4, pp. 111-120 das notas de aula): Identidades vetoriais: o produto vetorial, o produto misto e o produto vetorial duplo – recapitulação (operador
 de Hodge), produto vetorial de
de Hodge), produto vetorial de 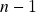 vetores em
vetores em 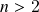 dimensões: definição em termos de Álgebra Exterior e propriedades. Fórmula do determinante (fórmula de Laplace) e interpretação geométrica do produto vetorial, justificativa geométrica do determinante como volume de um paralelepípedo
dimensões: definição em termos de Álgebra Exterior e propriedades. Fórmula do determinante (fórmula de Laplace) e interpretação geométrica do produto vetorial, justificativa geométrica do determinante como volume de um paralelepípedo  -dimensional (produto misto). Produto vetorial duplo à direita e à esquerda: definição em termos de Álgebra Exterior em
-dimensional (produto misto). Produto vetorial duplo à direita e à esquerda: definição em termos de Álgebra Exterior em 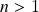 dimensões e propriedades. Componentes numa base ortonormal e fórmula alternativa. Não-associatividade do produto vetorial duplo.
dimensões e propriedades. Componentes numa base ortonormal e fórmula alternativa. Não-associatividade do produto vetorial duplo. - Aula 18 – 27.5 (vídeo, blog – Subseção I.3.3, pp. 104-111 das notas de aula): Operador
 de Hodge – recapitulação (produto escalar de
de Hodge – recapitulação (produto escalar de  -formas, identidade de Cauchy-Binet), definição e propriedades do operador
-formas, identidade de Cauchy-Binet), definição e propriedades do operador  de Hodge. Cálculo de
de Hodge. Cálculo de  em bases ortonormais de p-formas, inversa e ortogonalidade de
em bases ortonormais de p-formas, inversa e ortogonalidade de  . Exemplos em 2 e 3 dimensões. Aplicações (I) – cálculo de determinantes (fórmula de Laplace) e inversas de matrizes.
. Exemplos em 2 e 3 dimensões. Aplicações (I) – cálculo de determinantes (fórmula de Laplace) e inversas de matrizes. - Aula 17 – 20.5 (vídeo, blog – Subseção I.3.3, pp. 93-102 das notas de aula): Produto exterior (continuação): definição (recapitulação) e propriedades – bilinearidade, comutatividade graduada e associatividade. Produto exterior com mais de dois fatores. Caso particular do produto exterior de
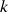 1-formas, isomorfismos musicais e versão geral da identidade de Cauchy-Binet.
1-formas, isomorfismos musicais e versão geral da identidade de Cauchy-Binet. - Aula 16 – 15.5 (vídeo, blog – Subseção I.3.3, pp. 92-97 das notas de aula): Álgebra Exterior (continuação): produto escalar e bases ortonormais em espaços de
 -formas e
-formas e  -vetores: recapitulação, invariância por mudança de bases ordenadas ortonormais, lema de Riesz e isomorfismos musicais para
-vetores: recapitulação, invariância por mudança de bases ordenadas ortonormais, lema de Riesz e isomorfismos musicais para  -formas e
-formas e  -vetores, relação entre produtos escalares de
-vetores, relação entre produtos escalares de  -formas e
-formas e  -vetores. Produto exterior: definição em termos da alternação do produto tensorial de uma
-vetores. Produto exterior: definição em termos da alternação do produto tensorial de uma  -forma e uma
-forma e uma 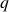 -forma, expressão alternativa em termos de
-forma, expressão alternativa em termos de 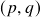 -embaralhamentos.
-embaralhamentos. - Aula 15 – 13.5 (vídeo, blog – Subseções I.3.2 e I.3.3, pp. 86-93 das notas de aula): Álgebra Exterior (continuação): espaços vetoriais de
 -formas.
-formas.  -vetores – definição, operações vetoriais, dualidade entre espaços de
-vetores – definição, operações vetoriais, dualidade entre espaços de  -formas e espaços de
-formas e espaços de  -vetores. Produto escalar e bases ortonormais em espaços de
-vetores. Produto escalar e bases ortonormais em espaços de  -formas e
-formas e  -vetores.
-vetores. - Aula 14 – 8.5 (vídeo, blog – Subseção I.3.2, pp. 80-86 das notas de aula): Álgebra Exterior (continuação): determinante de uma transformação linear: definição (recapitulação), propriedades básicas (adjunta, produto, identidade e inversa). Pares de bases ordenadas o.n. com mesma orientação e orientações opostas, transformações lineares que preservam orientação e que invertem orientação. Volumes de paralelepípedos
 -dimensionais: definição, identidades de Lagrange e de Cauchy-Binet. Projeção ortogonal de paralelepípedos
-dimensionais: definição, identidades de Lagrange e de Cauchy-Binet. Projeção ortogonal de paralelepípedos  -dimensionais sobre subespaços vetoriais
-dimensionais sobre subespaços vetoriais  -dimensionais.
-dimensionais. - Aula 13 – 6.5 (vídeo, blog – Subseção I.3.2, pp. 76-81 das notas de aula): Álgebra Exterior (continuação): permutações e sinal de uma permutação, ação de permutações em
 -formas (recapitulação). Expressão de uma
-formas (recapitulação). Expressão de uma  -forma em termos de uma base o.n..
-forma em termos de uma base o.n..  -formas e determinantes: bases ordenadas e bases ordenadas o.n., função determinante associada a uma base ordenada o.n.. Determinante de uma transformação linear: expressão em termos de uma função determinante, independência de base ordenada o.n., determinante de uma matriz.
-formas e determinantes: bases ordenadas e bases ordenadas o.n., função determinante associada a uma base ordenada o.n.. Determinante de uma transformação linear: expressão em termos de uma função determinante, independência de base ordenada o.n., determinante de uma matriz. - Aula 12 – 29.4 (vídeo, blog – Subseção I.3.2, pp. 72-77 das notas de aula): Álgebra Exterior:
 -formas, permutações e determinantes –
-formas, permutações e determinantes –  -formas (recapitulação): definição e propriedades, expressão em termos de uma base ortonormal. Permutações e sinal de uma permutação. Transposições e decomposição de uma permutação em um produto de transposições (enunciado). Ação de permutações em
-formas (recapitulação): definição e propriedades, expressão em termos de uma base ortonormal. Permutações e sinal de uma permutação. Transposições e decomposição de uma permutação em um produto de transposições (enunciado). Ação de permutações em  -formas.
-formas. - Aula 11 – 24.4 (vídeo, blog – Subseções I.3.1 e I.3.2, pp. 61-72 das notas de aula): Determinantes, formas de volume e
 -formas – motivação: área de um paralelogramo, formas de volume em duas dimensões como área da projeção ortogonal de um paralelogramo sobre um subespaço vetorial, orientação de uma forma de volume bidimensional.
-formas – motivação: área de um paralelogramo, formas de volume em duas dimensões como área da projeção ortogonal de um paralelogramo sobre um subespaço vetorial, orientação de uma forma de volume bidimensional.  -formas: definição e propriedades, expressão em termos de uma base ortonormal. Interlúdio: permutações e sinal de uma permutação (prévia da aula 12).
-formas: definição e propriedades, expressão em termos de uma base ortonormal. Interlúdio: permutações e sinal de uma permutação (prévia da aula 12). - Aula 10 – 22.4 (vídeo, blog – Subseção I.2.5, pp. 55-61 das notas de aula): Revisão de Álgebra Linear (continuação) – Teorema do Núcleo e da Imagem (demonstração). Aplicação ao Lema de Riesz. Determinantes, formas de volume e
 -formas (prévia da Aula 11).
-formas (prévia da Aula 11). - Aula 9 – 13.3 (presencial – Subseção I.2.5, pp. 53-55 das notas de aula): Revisão de Álgebra Linear (continuação) – imagem e imagem inversa de uma transformação linear, núcleo e imagem de uma transformação linear. Caracterização de sobrejetividade e injetividade de uma transformação linear em termos de seu núcleo e imagem e em termos de sua ação sobre bases. Nulidade e posto de uma transformação linear: o Teorema do Núcleo e da Imagem (enunciado).
- Aula 8 – 11.3 (presencial – Subseção I.2.5, pp. 46-53 das notas de aula): Revisão de Álgebra Linear (continuação) – transformações lineares e 1-formas (continuação): operações matriciais e sua correspondência com operações sobre transformações lineares. Mudanças de base e seu efeito sobre a matriz de uma transformação linear.
- Aula 7 – 6.3 (presencial – Subseção I.2.5, pp. 38-46 das notas de aula): Revisão de Álgebra Linear (continuação) – transformações lineares e 1-formas: definição e exemplos. Soma vetorial, multiplicação escalar e composição / produto de transformações lineares. Determinação de uma transformação linear pelos seus valores numa base, matriz de uma transformação linear, lema de Riesz.
- Aula 6 – 4.3 (presencial – Subseção I.2.4, pp. 31-38 das notas de aula): Revisão de Álgebra Linear (continuação) – produtos escalares (continuação): demonstração da desigualdade de Cauchy-Schwarz. Interpretação geométrica do produto escalar: componente de um vetor ao longo de outro, projeção ortogonal ao longo de um subespaço como minimizador de distância euclidiana. Construção de bases ortonormais: ortonormalização de Gram-Schmidt.
- Aula 5 – 28.2 (presencial – Subseção I.2.4, pp. 30-33 das notas de aula): Prova 1 (conteúdo: aula 1 a aula 4, até dimensão de um espaço vetorial, correspondendo à Lista 1). Revisão de Álgebra Linear (continuação) – produtos escalares (continuação): norma e distância euclidianas, ângulo entre vetores, desigualdade de Cauchy-Schwarz (enunciado).
- Aula 4 – 21.2 (presencial – Subseções I.2.3 e I.2.4, pp. 22-30 das notas de aula): Revisão de Álgebra Linear (continuação) – bases finitas, dimensão de um espaço vetorial. Produtos escalares – o produto escalar canônico de
 , axiomas do produto escalar. Produtos escalares abstratos – definição. Produto escalar associado a uma base, bases ortogonais e ortonormais.
, axiomas do produto escalar. Produtos escalares abstratos – definição. Produto escalar associado a uma base, bases ortogonais e ortonormais. - Aula 3 – 19.2 (presencial – Subseção I.2.3, pp. 15-22 das notas de aula): Revisão de Álgebra Linear (continuação) – combinações lineares e (in)dependência linear, conjuntos linearmente (in)dependentes, exemplos. Subespaços vetoriais gerados por um subconjunto de vetores. Bases – definição, exemplos e contra-exemplos. Bases canônicas.
- Aula 2 – 14.2 (presencial, blog – Subseções I.2.2 e I.2.3, pp. 6-15 das notas de aula): Revisão de Álgebra Linear – operações vetoriais de
 (soma vetorial, multiplicação escalar), axiomas de espaço vetorial. Espaços vetoriais – definição e exemplos (
(soma vetorial, multiplicação escalar), axiomas de espaço vetorial. Espaços vetoriais – definição e exemplos ( , espaços de funções a valores em
, espaços de funções a valores em  e a valores num espaço vetorial). Subespaços vetoriais – definição, exemplos e contra-exemplos.
e a valores num espaço vetorial). Subespaços vetoriais – definição, exemplos e contra-exemplos. - Aula 1 – 12.2 (presencial, blog – Seção I.1, pp. 1-5 das notas de aula): informações sobre a estrutura do curso (formato presencial pré-ECE). Motivação e objetivos: como seria uma versão do Teorema Fundamental do cálculo para funções de várias variáveis? Campos vetoriais e fluxos – uma descrição informal.
Bibliografia
Listamos aqui os textos que seguiremos mais de perto.
- Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969. Uma versão online gratuita dos dois volumes em inglês pode ser encontrada aqui).
- Notas de aula serão disponibilizadas aqui à medida que o conteúdo for apresentado.
(Observação: o links do livro disponibilizado acima parte de um servidor que, em princípio, oferece tais materiais legalmente. Se for comprovado que este não é o caso, os links serão retirados sem aviso prévio)
Textos suplementares (listados na bibliografia das notas de aula):
- R. Bott, L. Tu, Differential Forms in Algebraic Topology. Springer-Verlag, 1995.
- R. W. R. Darling, Differential Forms and Connections. Cambridge University Press, 1994.
- J. J. Duistermaat, J. A. C. Kolk, Multidimensional Real Analysis I – Differentiation; II – Integration. Cambridge University Press, 2004.
- H. Flanders, Differential Forms with Applications to the Physical Sciences. Academic Press, 1963.
- N. J. Hicks, Notes on Differential Geometry. Van Nostrand Reinhold, 1971.
- E. L. Lima, Curso de Análise, Volume 2 (décima primeira edição). Projeto Euclides, IMPA, 2009.
- L. Tu, An Introduction to Manifolds (2a. edição). Springer-Verlag, 2011.
Recomendações e material didático suplementar
Faremos uso tácito de conceitos vistos na disciplina BCN0407 – Funções de Várias Variáveis. Recomendamos fortemente que o aluno com dificuldades nos tópicos dessa disciplina faça uma revisão destes, pois isto não será feito em aula exceto nos casos previstos no Roteiro.
Estrutura das atividades da disciplina
As aulas 1 a 9, ministradas de 12.2 a 13.3, foram presenciais, e seu conteúdo pode ser encontrado tanto na seção “Roteiro” abaixo como mais detalhadamente na seção “Aulas” acima. Para facilitar a recapitulação desse conteúdo, apontamos os trechos correspondentes a cada aula nas notas de aula.
O conteúdo do restante da disciplina será apresentado online de maneira assíncrona a partir de 22.4, envolvendo aulas em vídeo e em formato escrito de blog. A estrutura das aulas seguirá o seguinte formato:
- Aulas em vídeo: aulas em vídeo serão postadas na plataforma Internet Archive às quartas e sextas-feiras.
- Aulas em blog: o material de cada aula em vídeo será disponibilizado também em formato escrito, como postagens num blog criado nesta página para tal finalidade, preferencialmente no mesmo dia da aula em vídeo correspondente. Cada postagem do blog deverá corresponder a uma aula, cujo espaço de comentários será destinado às dúvidas referentes àquela aula. É importante que cada aluno se identifique com o seu nome completo ao postar dúvidas no blog, pois isso fará parte do controle de frequência (ver seção “Controle de frequência” abaixo).
Os links para o vídeo e a postagem de blog correspondentes a cada aula serão disponibilizados na seção “Aulas” acima.
Avaliação
A avaliação durante o período pré-ECE (12.2 a 13.3) foi planejada para ser feita por meio de cinco (5) provas curtas, de 45 minutos de duração, a serem aplicadas com um interstício de cerca de duas semanas entre uma prova e outra (mais feriados). A resolução de cada prova seria feita em sala de aula imediatamente após seu término, e o restante da aula retomaria a discussão teórica. Apenas a Prova 1 foi aplicada nesse esquema antes da suspensão das atividades presenciais.
A partir do início do período de ECE em 20.4, a avaliação passará a ser feita da seguinte maneira:
- A Prova 1, aplicada no período pré-ECE, contará como 20% da média final, peso igual ao de cada uma das cinco provas originalmente previstas na avaliação no período pré-ECE.
- Haverá uma prova final presencial que contará como 50% da média final, a ser aplicada no período de complementação presencial do ECE, que é um período de três semanas a ser agendado para após o término do período de isolamento social e a retomada das atividades presenciais nos campi da UFABC. O conteúdo dessa prova será divulgado no início de maio, e a sua data será divulgada assim que o período de complementação presencial for fixado.
- Os 30% restantes da média final serão baseados no envio das resoluções das listas de exercícios. A resolução de cada lista deverá ser digitalizada (aplicativos gratuitos para a digitalização de documentos por câmera de smartphones são sugeridos abaixo) e enviada em um único arquivo PDF (outros formatos não serão aceitos) pelo Moodle durante os períodos estabelecidos e previamente divulgados nessa plataforma.
- Aos alunos que não puderam comparecer à Prova 1 no período pré-ECE ou não puderem comparecer à prova final presencial, será dada a possibilidade de fazer uma prova substitutiva presencial varrendo o conteúdo correspondente à prova perdida no período de complementação presencial, em data a ser marcada após a prova final presencial. Para tal, é exigido que seja apresentado presencialmente um atestado formal por escrito justificando a ausência. Caso isso já não tenha sido feito no período pré-ECE, o atestado deve ser entregue durante o período de complementação presencial até a data da prova substitutiva. Preferencialmente o original deve ser entregue – caso o mesmo seja necessário para justificar a ausência em provas de outras disciplinas, pede-se que seja enviada cópia digitalizada e o original seja apresentado apenas para conferência.
- A prova de recuperação (presencial) será marcada após a prova substitutiva (respeitando o interstício mínimo de 72 horas entre sua aplicação e a divulgação dos conceitos preliminares) e varrerá o conteúdo do quadrimestre inteiro. Apenas alunos com conceitos preliminares D e F terão direito a fazê-la. A média final é calculada substituindo a prova final presencial pelo maior valor entre esta e a prova de recuperação.
Média preliminar ( = Mp – nota da Prova 1 = P1; média das listas = Ml; nota da prova final = Pf):
Mp = 0,2 P1 + 0,3 Ml + 0,5 Pf
Média final ( = Mf – nota da prova de recuperação = Rec):
Mf = 0,2 P1 + 0,3 Ml + 0,5 max(Pf,Rec)
Critério de conversão de média preliminar (Mp) / final (Mf) para conceito preliminar (Cp) / final (Cf):
Cp (resp. Cf) = F – Mp (resp. Mf) < 4,5;
Cp (resp. Cf) = D – Mp (resp. Mf) = 4,5-5,2;
Cp (resp. Cf) = C – Mp (resp. Mf) = 5,3-6,9;
Cp (resp. Cf) = B – Mp (resp. Mf) = 7,0-8,4;
Cp (resp. Cf) = A – Mp (resp. Mf) = 8,5-10,0.
Sugestões de ferramentas gratuitas para digitalização de documentos em formato PDF usando a câmera de smartphones:
- Adobe Scan (Android, iOS);
- vFlat (somente para Android);
- Microsoft Office Lens (Android, iOS);
- Google Drive (ferramenta de digitalização integrada à nuvem da Google – aviso: esse recurso é mais limitado que o dos apps dedicados listados acima! Somente para Android).
Calendário de divulgação de seleções de exercícios a serem entregues:
- Lista 1: 8.5 – entrega até 11.5
- Lista 2: 15.5 – entrega até 18.5
- Lista 3 (parte 1): 5.6 – entrega até 8.6
- Lista 3 (parte 2): 26.6 – entrega até 29.6
- Lista 4: a agendar para o período de avaliação presencial pós-ECE
Listas de exercícios
É extremamente importante que os alunos façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!
Monitoria, atendimento online e plantão de dúvidas
O Moodle continuará servindo como plataforma online para envio e atendimento de dúvidas pelos monitores e/ou docentes da disciplina. Para mais informações, ver a página de monitoria de CVT do Gradmat.
Há também uma monitoria por videoconferência às sextas-feiras das 12h00 às 14h00 com o monitor Victor Guedes.
Haverá um plantão de dúvidas em vídeoconferência às quartas-feiras e sextas-feiras das 19h00 às 21h00, usando a plataforma Jitsi Meet. Ela pode ser acessada por qualquer navegador de páginas Web (e.g. Google Chrome, Mozilla Firefox) ou pelo app Jitsi Meet para smartphones (Android, iOS).
O plantão terá início em caráter experimental no dia 22.4 – por razões de segurança, o link para a sala de reunião será divulgado por email e pelo Moodle no máximo 30 minutos antes do início de cada reunião.
Os alunos que participarem de um plantão de dúvidas por videoconferência deverão se identificar na sala de reunião do Jitsi Meet pelo nome completo, para fins de controle de presença.
Controle de frequência
Como exigido pela Resolução ConsEPE no. 239/2020, os docentes que optaram pelo ECE devem definir no plano de ensino algum tipo de controle de presença dos alunos através das atividades assíncronas. Levando em conta a dificuldade inerente desse tipo de controle por tal meio, isso será feito aqui de diferentes maneiras:
- Presença nas aulas presenciais no período pré-ECE;
- Participação nas aulas por meio da postagem de dúvidas em blog e no Moodle, incluindo monitoria;
- Envio de resoluções das listas de exercícios solicitadas para fins de avaliação (ver seção “Avaliação” acima).
Para complementar o controle de frequência por atividades assíncronas e assim ter uma imagem mais completa da participação dos alunos nas atividades da disciplina, será também controlada a presença nos plantões de dúvidas por videoconferência.
Roteiro
Seguiremos de maneira aproximada o cronograma sugerido para o curso de CVT pelo Gradmat, com algumas modificações. Os tópicos varridos até a suspensão das atividades presenciais foram os seguintes:
- Revisão de Álgebra Linear em
 : vetores, (sub)espaços vetoriais, dependência linear e bases. Matrizes e transformações lineares. Produto escalar, norma e distância euclideanas, lema de Riesz.
: vetores, (sub)espaços vetoriais, dependência linear e bases. Matrizes e transformações lineares. Produto escalar, norma e distância euclideanas, lema de Riesz.
Os demais tópicos, a serem varridos durante o período de ECE, são os seguintes:
- Determinantes, multivetores e formas de volume orientadas associadas a uma base. Produto exterior. Mudanças de base e seu efeito sobre multivetores e formas de volume. Operador de Hodge sobre formas de volume, produto vetorial.
- Análise vetorial: aplicações diferenciáveis e campos vetoriais, operadores gradiente, divergente, rotacional (em
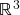 ) e laplaciano. Interpretação geométrica do gradiente. Formas diferenciais, derivada exterior e coderivada exterior. Operadores gradiente, divergente, rotacional e laplaciano revisitados.
) e laplaciano. Interpretação geométrica do gradiente. Formas diferenciais, derivada exterior e coderivada exterior. Operadores gradiente, divergente, rotacional e laplaciano revisitados. - Curvas, superfícies e subvariedades: caso parametrizado, cartas locais e descrição implícita, espaços tangentes / normais e campos vetoriais tangentes / normais. Parametrizações especiais: coordenadas polares, cilíndricas e esféricas.
- Integrais de caminho, de superfície e em subvariedades. Caso parametrizado, mudança de variáveis e partições de unidade. (Ou: por que precisamos de formas de volume?)
- Teorema Fundamental do Cálculo em várias variáveis: o teorema geral de Stokes. Casos particulares em duas e três dimensões: teoremas de Green, Gauss e Stokes clássico. Interpretação geométrica do divergente e do rotacional: fluxo e circulação de campos vetoriais. Interpretação geométrica do laplaciano: potencial de Newton e decomposição de Helmholtz de campos vetoriais em
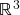 .
. - Tópicos suplementares (se houver tempo): derivada covariante em subvariedades, geodésicas e curvatura, campos tensoriais. Aplicações em Física: fluidos, Eletromagnetismo e Relatividade.

