Plano de ensino – AlgLin – QS6 – 2q’22

Author: Jun Lu; License: Creative Commons Attribution 4.0 International

Este é o plano de ensino para a disciplina MCTB001 – Álgebra Linear (AlgLin) conforme ministrada remotamente no segundo quadrimestre letivo de 2022 = sexto Quadrimestre Suplementar (QS) para a turma A Noturno – campus Santo André, nos seguintes horários:

2as. feiras e 5as. feiras 19h00-21h00, 4as. feiras 21h00-23h00.

Aqui encontram-se informações específicas sobre a turma acima.

Novidades

Notícias recentes sobre o funcionamento do curso serão postadas aqui.

(5.6.22) A primeira versão das notas de aula está disponível. Estas serão atualizadas gradativamente.

Aulas

Os links para o material de cada aula (vídeo e/ou blog), acompanhados de uma breve descrição desta, serão listados aqui.

Aula 27 – 25.8.22 (vídeo) – Sistemas lineares (iv): exemplos de uso do algoritmo de eliminação gaussiana ( = escalonamento de matrizes). Recapitulação – algoritmo de eliminação gaussiana (descrição e resultado de sua ação sobre a matriz de uma transformação linear = forma escalonada em linhas (“row echelon form”)). Consequências do algoritmo: critério de existência e unicidade de soluções, critério de invertibilidade da transformação linear associada ao sistema. Exemplos de escalonamento: (1.) sistemas com solução única; (2.) sistemas sem solução; (3.) sistemas com mais de uma solução. O caso de transformações lineares invertíveis: inversão de matrizes por eliminação gaussiana (esboço) (ver preâmbulo da Lista 7).
Aula 26 – 22.8.22 (vídeo) – Sistemas lineares (iii): o algoritmo de eliminação gaussiana ( = escalonamento de matrizes). Recapitulação – forma abstrata e soluções de um sistema linear, sistemas lineares homogêneos e não-homogêneos, o sistema linear homogêneo associado a um sistema linear, princípio de superposição para sistemas lineares homogêneos, soluções particulares, solução geral de um sistema linear = solução particular + solução geral do sistema linear homogêneo associado, base de soluções de um sistema linear homogêneo, sistemas lineares em forma matricial, variáveis e equações, operações elementares sobre uma base do contradomínio da transformação linear associada a um sistema linear e seu efeito sobre a matriz desta. Algoritmo de eliminação gaussiana: objetivo, descrição e resultado de sua ação sobre a matriz de uma transformação linear = forma escalonada em linhas (“row echelon form”). Consequências do algoritmo: critério de existência e unicidade de soluções, solução geral (ver preâmbulo da Lista 7).
Aula 25 – 15.8.22 (vídeo) – Sistemas lineares (ii): operações elementares. Recapitulação – forma abstrata e soluções de um sistema linear, sistemas lineares homogêneos e não-homogêneos, o sistema linear homogêneo associado a um sistema linear, princípio de superposição para sistemas lineares homogêneos, soluções particulares e solução geral de um sistema linear = solução particular + solução geral do sistema linear homogêneo associado, base de soluções de um sistema linear homogêneo, sistemas lineares em forma matricial, variáveis e equações. A ação de transformações lineares invertíveis no contradomínio da transformação linear associada a um sistema linear. Operações elementares sobre uma base do contradomínio, suas matrizes nessa base e seu efeito sobre a matriz de uma transformação linear.
Aula 24 – 11.8.22 (vídeo) – Sistemas lineares (i): forma abstrata, soluções de um sistema linear. Existência e unicidade de soluções, caracterização em termos da imagem e do núcleo da transformação linear associada ao sistema linear. Sistemas lineares homogêneos e não-homogêneos, o sistema linear homogêneo associado a um sistema linear, princípio de superposição para sistemas lineares homogêneos. Soluções particulares, solução geral de um sistema linear = solução particular + solução geral do sistema linear homogêneo associado, base de soluções de um sistema linear homogêneo. O caso de dimensão finita: sistemas lineares em forma matricial, variáveis e equações. O caminho para a solução de sistemas lineares: sistemas lineares equivalentes, a ação de transformações lineares invertíveis no contradomínio da transformação linear associada a um sistema linear.
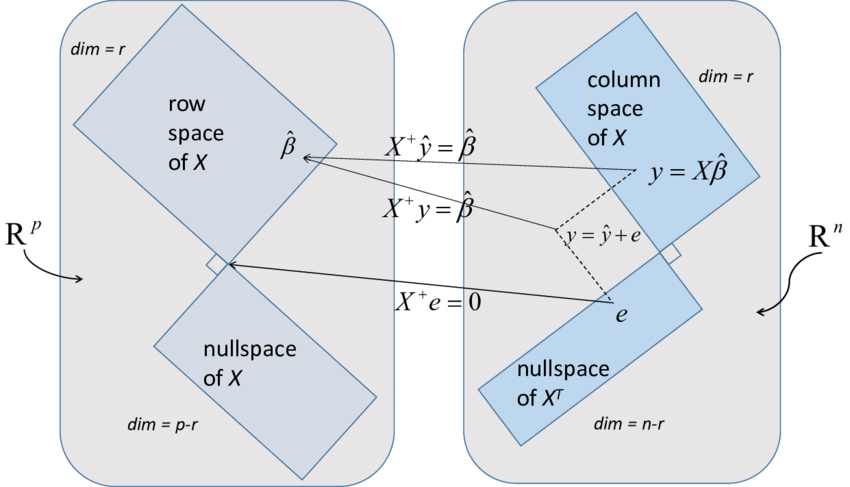
Aula 23 – 10.8.22 (vídeo) – Transformações lineares (viii): projeções lineares e pseudoinversas. Definição e propriedades de projeções lineares, núcleo e imagem, correspondência biunívoca entre projeções lineares e pares de subespaços vetoriais mutuamente complementares. Interlúdio: núcleo e imagem da adjunta de uma transformação linear, caracterização de projeções ortogonais. Pseudoinversas de transformações lineares: definição, exemplos (o caso de transformações lineares bijetoras), projeções associadas a uma pseudoinversa, pseudoinversas com as mesmas projeções associadas. O caso de projeções ortogonais, pseudoinversa de Moore-Penrose. Aplicações de pseudoinversas: regressão linear.
Aula 22 – 8.8.22 (vídeo) – Transformações lineares (vii): o Teorema do Núcleo e da Imagem (continuação). Recapitulação – imagem e imagem inversa de subconjuntos por transformações lineares (definição, o caso de subconjuntos unitários, o caso de subespaços vetoriais), núcleo e imagem de uma transformação linear. O caso de domínios com dimensão finita: o Teorema do Núcleo e da Imagem – enunciado e prova, posto e nulidade de uma transformação linear. Consequências do Teorema do Núcleo e da Imagem: caracterização dimensional de injetividade, sobrejetividade e bijetividade de uma transformação linear, efeito de transformações lineares sobre conjuntos linearmente independente e sobre bases (páginas 49 a 52 das notas de aula).
Aula 21 – 4.8.22 (vídeo) – Transformações lineares (vi): o efeito de mudança de bases sobre a matriz de uma transformação linear – transformações lineares implementando mudanças de base e suas matrizes ( = matrizes de mudança de base), relação entre as matrizes de uma transformação linear em dois pares de bases, o caso de bases ortonormais. Imagem e imagem inversa de um subconjunto por uma transformação linear: definição, o caso de imagens inversas de subconjuntos unitários. Imagens e imagens inversas de subespaços vetoriais por transformações lineares como subespaços vetoriais, núcleo e imagem de uma transformação linear. Caracterização da injetividade de uma transformação linear em termos de seu núcleo. O caso de domínios com dimensão finita: o Teorema do Núcleo e da Imagem (enunciado), posto e nulidade de uma transformação linear (páginas 48 a 51 das notas de aula).
Aula 20 – 3.8.22 (vídeo) – Transformações lineares (v): recapitulação – determinação de uma transformação linear por seus valores numa base, vetor-coluna ( = matriz com uma única coluna) de um vetor numa base, forma matricial da ação de transformações lineares num par de bases, a matriz de uma transformação linear. Forma matricial das operações algébricas sobre transformações lineares: operações vetoriais pontuais, produto e inversa. Transposição de matrizes e a adjunta de uma transformação linear – identidade fundamental. O efeito de mudança de bases sobre a matriz de uma transformação linear – enunciado (páginas 43 a 48 das notas de aula).
Aula 19 – 1.8.22 (vídeo) – Transformações lineares (iv): recapitulação – determinação de uma transformação linear por seus valores numa base, vetor-coluna ( = matriz com uma única coluna) de um vetor numa base, forma matricial da ação de transformações lineares num par de bases, a matriz de uma transformação linear. Forma matricial das operações algébricas sobre transformações lineares: operações vetoriais pontuais e produto. Consequências da identificação de transformações lineares com suas respectivas matrizes num par de bases: (1.) associatividade e bilinearidade da multiplicação matricial; (2.) não-commutatividade do produto de transformações lineares; (3.) o caso de transformações lineares invertíveis – a matriz inversa. Transposição de matrizes, a adjunta de uma transformação linear com respeito a um par de produtos escalares no domínio e no contradomínio (páginas 43 a 47 das notas de aula).
Aula 18 – 25.7.22 (vídeo) – Transformações lineares (iii): recapitulação – espaços de transformações lineares, funcionais lineares e o dual de um espaço vetorial, operações algébricas sobre transformações lineares: (operações vetoriais pontuais, produto = composição). Inversas de transformações lineares bijetoras. Determinação de uma transformação linear por seus valores numa base. A matriz de uma transformação linear: vetor-coluna ( = matriz com uma única coluna) de um vetor numa base, forma matricial da ação de transformações lineares num par de bases (páginas 41 a 44 das notas de aula).
Aula 17 – 21.7.22 (vídeo) – Transformações lineares (ii): recapitulação – definição e axiomas, notação e consequências dos axiomas, espaços de transformações lineares, funcionais lineares e o dual de um espaço vetorial. Exemplos e contraexemplos de transformações lineares (ii): zero, aplicações constantes, identidade, o produto escalar com um vetor fixo, a identificação de um espaço vetorial de dimensão $n$ com $\mathbb{R}^n$ . Operações algébricas sobre transformações lineares: operações vetoriais pontuais, produto ( = composição) (páginas 39 a 42 das notas de aula).
Aula 16 – 18.7.22 (vídeo) – Produtos escalares (v): recapitulação – ortogonalizacão e ortonormalização de bases, o algoritmo de Gram-Schmidt. Exemplo de aplicação do algoritmo de Gram-Schmidt. O complemento ortogonal de um subespaço vetorial e sua projeção ortogonal. Transformações lineares (i): definição e axiomas, notação, espaços de transformações lineares. Funcionais lineares e o dual de um espaço vetorial. Exemplos de transformações lineares (i): zero, múltiplos da identidade, o produto escalar com um vetor fixo (páginas 36 a 40 das notas de aula).
Aula 15 – 14.7.22 (vídeo) – Produtos escalares (iv): projeções ortogonais ao longo de um subespaço vetorial – recapitulação (motivação unidimensional), definição em termos de uma base ortogonal do subespaço vetorial e propriedades (imagem, idempotência, linearidade e ortogonalidade). A projeção ortogonal de um vetor ao longo de um subespaço vetorial como o vetor no último mais próximo desse vetor, independência da escolha de base ortogonal. Ortogonalizacão e ortonormalização de bases: o algoritmo de Gram-Schmidt (páginas 34 a 37 das notas de aula).
Aula 14 – 11.7.22 (vídeo) – Produtos escalares (iii): Geometria do produto escalar – distância e norma (euclidianas), ângulo entre vetores (lei dos cossenos). A desigualdade de Cauchy-Schwarz – enunciado e prova, o caso de igualdade. Consequências da desigualdade de Cauchy-Schwarz – propriedades da norma e da distância (não-degenerescência, homogeneidade e desigualdade triangular), interpretação geométrica do ângulo entre vetores (vetores linearmente dependentes, vetores ortogonais). Interpretação geométrica das componentes de um vetor numa base ortonormal (páginas 31 a 34 das notas de aula).
Aula 13 – 7.7.22 (vídeo) – Produtos escalares (ii): recapitulação – definição abstrata de produto escalar ( = produto interno) num espaço vetorial, consequências dos axiomas de produto escalar (bilinearidade, produto escalar com o vetor zero), ortogonalidade e ortonormalidade, subconjuntos ortogonais e ortonormais, normalização de um conjunto ortogonal que não contém o zero. Prova da independência linear de subconjuntos ortogonais não-vazios que não contém o zero, componentes de um vetor em bases ortogonais e ortonormais. Unicidade do produto escalar associado a uma base. Geometria do produto escalar: a desigualdade de Cauchy-Schwarz (enunciado) (páginas 29 a 32 das notas de aula).
Aula 12 – 4.7.22 (vídeo) – Produtos escalares (i): motivação – o produto escalar canônico em $\mathbb{R}^n$ , axiomas de produto escalar. Definição abstrata de produto escalar ( = produto interno) num espaço vetorial. Consequências dos axiomas de produto escalar – bilinearidade. Exemplos de produtos escalares: (1.) o produto escalar canônico em $\mathbb{R}^n$ ; (2.) Espaços de polinômios (integral de produto pontual) (3.) O produto escalar associado a uma base finita. Ortogonalidade e ortonormalidade, subconjuntos ortogonais e ortonormais, independência linear de subconjuntos ortogonais não-vazios que não contém o zero (páginas 29 e 30 das notas de aula).
Aula 11 – 1.7.22 (reposição da aula de 29.6.22 – vídeo) – (In)dependência linear e bases de um espaço vetorial (iv): recapitulação – bases de um espaço vetorial: definição, componentes de um vetor numa base ( = sistema de “coordenadas lineares”). Subespaços vetoriais linearmente independentes – definição, critério de independência linear de subespaços vetoriais em termos de suas interseções. Somas diretas de subespaços vetoriais, subespaços vetoriais complementares a um subespaço vetorial dado.
Aula 10 – 30.6.22 (vídeo) – (In)dependência linear e bases de um espaço vetorial (iii): recapitulação – bases de um espaço vetorial: definição, componentes de um vetor numa base ( = sistema de “coordenadas lineares”) e (contra)exemplos – (1.) a base canônica de $\mathbb{R}^n$ ; (2.) bases canônicas de espaços de matrizes; (3.) o caso de espaços de funções. O caso de bases finitas – independência do número de vetores numa base finita ( = número de “coordenadas lineares”) = dimensão do espaço vetorial. 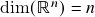Espaços vetoriais de dimensão finita e infinita: definição e exemplos – (1.) $\dim(\mathbb{R}^n)=n$ ; (2.) espaços de funções a valores reais tem dimensão (in)finita se e somente se seu domínio comum é (in)finito. Espaços vetoriais de dimensão finita: critério da dimensão para bases, construção indutiva de bases e bases adaptadas a um subespaço vetorial dado (páginas 22 a 27 das notas de aula).
Aula 9 – 27.6.22 (vídeo) – (In)dependência linear e bases de um espaço vetorial (ii): recapitulação – subconjuntos linearmente dependentes e linearmente independentes (definição), o subespaço (vetorial) gerado por um subconjunto de um espaço vetorial (definição, ação das operações vetoriais sobre os coeficientes de combinações lineares), o caso de subconjuntos linearmente independentes (unicidade da representação de um vetor no subespaço gerado). Bases de um espaço vetorial: definição, componentes de um vetor numa base ( = sistema de “coordenadas lineares”) e (contra)exemplos – (1.) a base canônica de $\mathbb{R}^n$ ; (2.) bases canônicas de espaços de matrizes; (3.) o caso de espaços de funções. O caso de bases finitas – independência do número de vetores numa base finita ( = número de “coordenadas lineares”) = dimensão do espaço vetorial (páginas 19 a 25 das notas de aula).
Aula 8 – 23.6.22 (vídeo) – (In)dependência linear e bases de um espaço vetorial (i): recapitulação – combinações lineares (definição, combinações lineares triviais e não-triviais), (in)dependência linear de listas finitas de vetores. Subconjuntos linearmente dependentes e linearmente independentes: definição, propriedades e exemplos, o caso de subconjuntos finitos. O subespaço (vetorial) gerado por um subconjunto de um espaço vetorial: definição, ação das operações vetoriais sobre os coeficientes de combinações lineares. O caso de subconjuntos linearmente independentes: unicidade da representação de um vetor no subespaço gerado, bases e componentes de um vetor numa base ( = sistema de “coordenadas lineares”) (páginas 19 a 22 das notas de aula).
Aula 7 – 22.6.22 (vídeo) – Combinações lineares e (in)dependência linear: recapitulação – somatória vetorial (definição recursiva, somatória ao longo de um conjunto finito e propriedades). Combinações lineares: definição, combinações lineares triviais e não-triviais. (In)dependência linear de listas finitas de vetores: definição e interpretação como (falta de) ambiguidade na escolha de “coordenadas lineares” (páginas 18 e 19 das notas de aula).
Aula 6 – 20.6.22 (vídeo) – Subespaços vetoriais (ii): recapitulação – definição e estrutura de espaço vetorial herdada do espaço vetorial ambiente. (Contra)exemplos e de subespaços vetoriais: subespaço trivial, espaços de soluções de sistemas lineares, espaços de polinômios, espaços de funções deriváveis e contínuas. Interlúdio: somatória vetorial – definição recursiva e propriedades (páginas 14 a 19 das notas de aula).
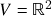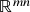Aula 5 – 15.6.22 (vídeo) – Exemplos de espaços vetoriais (ii): recapitulação – axiomas de espaço vetorial. Exemplos de espaços vetoriais (ii): recapitulação dos exemplos 1.)-5.) da aula 4; 6.) um contraexemplo $V=\mathbb{R}^2$ com uma candidata não-usual a soma vetorial; 7.) espaços de matrizes reais com $m$ linhas e $n$ colunas, identificação com $\mathbb{R}^{mn}$ . subespaços vetoriais (i): definição e estrutura de espaço vetorial herdada do espaço vetorial ambiente. Construções de subespaços vetoriais (i): interseções e somas de subespaços vetoriais, quando uniões de subespaços vetoriais falham em ser subespaços vetoriais (páginas 12 a 15 das notas de aula).
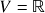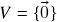Aula 4 – 13.6.22 (vídeo) – Espaços vetoriais (reais) (ii): recapitulação – axiomas de espaço vetorial e suas consequências. Exemplos de espaços vetoriais (i): 1.) $V=\mathbb{R}$ ; 2.) $V=\{\vec{0}\}$ (espaço vetorial trivial); 3.) 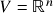$V=\mathbb{R}^n$ ; 4.) espaços de funções a valores reais, $\mathbb{R}^n$ como caso particular; 5.) espaços de funções a valores num espaço vetorial (páginas 11 a 13 das notas de aula).
Aula 3 – 9.6.22 (vídeo) – Espaços vetoriais (reais) (i): definição e axiomas. Consequências simples dos axiomas, analogias e diferenças das operações vetoriais com a soma e o produto de escalares (páginas 7 a 11 das notas de aula).
Aula 2 – 8.6.22 (vídeo) – Origem geométrica das operações vetoriais (ii): recapitulação – espaços afins e função deslocamento: definição e propriedades. Definição da soma vetorial e derivação de suas propriedades (comutatividade, associatividade, elemento neutro e oposto). Escalares como fatores de escala para vetores de deslocamento e multiplicação escalar: o caso de escalares naturais e inteiros, propriedades (distributividade com respeito às somas escalar e vetorial, associatividade, elemento neutro). Escalares racionais: como definir multiplicação escalar? Interpretação geométrica. O caso de escalares reais, o conceito de espaço vetorial (páginas 1 a 7 das notas de aula).
Aula 1 – 6.6.22 (vídeo) – Informações sobre o funcionamento do curso. Motivação: o que são espaços vetoriais e qual a sua importância? Origem geométrica das operações vetoriais (i): vetores de deslocamento num espaço de pontos (espaço afim), soma vetorial, axioma de comutatividade (páginas 1 a 4 das notas de aula).

Bibliografia

Listamos aqui os textos que seguiremos mais de perto.

Tom M. Apostol, Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996 (original em inglês: Calculus, Volume II – Second Edition. Wiley, 1969. Uma versão online gratuita dos dois volumes em inglês pode ser encontrada aqui).
Notas de aula serão disponibilizadas aqui à medida que o conteúdo for apresentado.

(Observação: o link do livro disponibilizado acima parte de um servidor que, em princípio, oferece tais materiais legalmente. Se for comprovado que este não é o caso, os links serão retirados sem aviso prévio)

A lista abaixo indica textos suplementares que podem ser de utilidade para o aluno.

Notas de aulas do Prof. Jerônimo C. Pellegrini (atualizadas periodicamente).
Howard Anton, Chris Rorres, Álgebra Linear com Aplicações (décima edição). Bookman, 2012 (original em inglês: Linear Algebra with Applications – 9th Edition. Wiley, 2005).
G. Strang, Introduction to Linear Algebra (5a. edição). Wellesley Cambridge Press, 2016.

Recomendações e material didático suplementar

É recomendado que o aluno tenha cursado anteriormente a disciplina BCN0404 – Geometria Analítica. Ocasionalmente, conceitos básicos da disciplina BCN0402 – Funções de Uma Variável – e.g. cálculo de integrais simples – podem ser empregados em exemplos.

Material suplementar – cursos online, vídeos:

MIT OpenCourseWare – 18.06SC Linear Algebra (Fall 2011) – Prof. Gilbert Strang
MIT OpenCourseWare – 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning (Spring 2018) – Prof. Gilbert Strang
MIT OpenCourseWare – RES.18-010 A 2020 Vision of Linear Algebra (Spring 2020) – Prof. Gilbert Strang
YouTube – Canal 3Blue1Brown – The essence of linear algebra – Introdução e playlist das aulas (16 vídeos)

Os cursos do Prof. Gilbert Strang no MIT são famosos pela abordagem inovadora, motivada por aplicações modernas da Álgebra Linear (representação e análise de dados, aprendizado de máquina, etc.) e que pode ser vista como complementar ao ponto de vista adotado neste curso, embora com vários pontos em comum. A série de vídeos The essence of linear algebra, por sua vez, busca trazer uma compreensão visual intuitiva dos conceitos básicos do assunto.

Estrutura das atividades da disciplina

As aulas terão um formato híbrido – serão disponibilizadas assincronamente três aulas por semana (menos o número de dias de feriado na semana em questão coincidindo com os dias do horário presencial) de acordo com a carga didática da disciplina, sendo que duas delas serão também transmitidas sincronamente nas seguintes datas e horários (exceto feriados – estes serão repostos no período de reposição seguindo o calendário acadêmico de 2022):

Segundas-feiras, 19h00-21h00;
Quintas-feiras, 19h00-21h00.

Em outras palavras, as aulas das quartas-feiras (originalmente previstas das 21h00 às 23h00) serão apenas gravadas e disponibilizadas assincronamente no mesmo dia. Reitero que a transmissão das aulas síncronas será gravada e também disponibilizada posteriormente de maneira assíncrona. O link para a sala de reunião (Google Meet) onde cada aula será transmitida será divulgado por email e pelo Moodle com no máximo 30 minutos de antecedência por razões de segurança. A entrada nas salas de reunião só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de segurança e controle da participação dos alunos. Para realizar o vinculamento, recomendo seguir o tutorial do NTI para o procedimento.

O objetivo das aulas síncronas é permitir (dentro das limitações da internet de cada aluno e do docente) uma maior participação dos alunos. Os links para os vídeos correspondentes a cada aula serão disponibilizados na lista de aulas acima.

Avaliação

A avaliação consistirá em dois tipos de atividades:

Duas provas (P₁, P₂) a serem aplicadas na plataforma Moodle, no seguinte formato: haverá uma janela temporal de 72 horas para a prova ser feita. Uma vez iniciada dentro desse período, o aluno terá até 3 horas para enviar a resolução (período suficiente para lidar com eventuais dificuldades no envio) ou até que a janela temporal se encerre (o que ocorrer primeiro). As provas são questionários de múltipla escolha a serem respondidos dentro do próprio Moodle, que efetuará a correção automaticamente.
Envio de resoluções de seleções de exercícios para cada uma das listas de exercícios (ver a seção “Listas de exercícios” abaixo para mais detalhes). As resoluções correspondentes a cada lista deverão também ser enviadas pelo Moodle dentro de uma janela temporal de 72 horas.

Haverá uma prova de recuperação a ser agendada para o início do terceiro quadrimestre letivo de 2022, no mesmo formato que a P₁ e a P₂ mas que cobrirá o conteúdo do curso inteiro.

Média preliminar: M_p = 0,25*(P₁+P₂) + 0,5*M_l , onde Ml é a média simples das resoluções das listas de exercícios.

Média final: M_f = 0,25*max(P₁+P₂ ,Rec+P₁, Rec+P₂) + 0,5*M_l

Critério de conversão de média preliminar (M_p) / final (M_f) para conceito preliminar (C_p) / final (C_f):

C_p (resp. C_f) = F – M_p (resp. M_f) < 4,5;
C_p (resp. C_f) = D – M_p (resp. M_f) = 4,5-5,2;
C_p (resp. C_f) = C – M_p (resp. M_f) = 5,3-6,9;
C_p (resp. C_f) = B – M_p (resp. M_f) = 7,0-8,4;
C_p (resp. Cf) = A – M_p (resp. M_f) = 8,5-10,0.

Sugestões de ferramentas gratuitas para digitalização de documentos em formato PDF usando a câmera de smartphones:

Adobe Scan (Android, iOS);
vFlat (somente para Android);
Microsoft Office Lens (Android, iOS);
Google Drive (ferramenta de digitalização integrada à nuvem da Google – aviso: esse recurso é mais limitado que o dos apps dedicados listados acima! Somente para Android).

Janelas das provas:

P1 – 00h00 de terça-feira, 26.7 às 23h59 de quinta-feira, 28.7;
P2 – 00h00 de quarta-feira, 1.9 às 23h59 de sexta-feira, 3.9;
Sub – janela a ser agendada (se necessário) na primeira semana de setembro de 2022;
Rec – a ser agendada no início do terceiro quadrimestre letivo de 2022.

Observo que, durante as janelas das provas, não haverá transmissão ou gravação de aulas, tampouco plantões de dúvidas por videoconferência. Nesse período, dúvidas poderão ser postadas no fórum de dúvidas do Moodle ou por email. A Sub só estará acessível aos alunos que apresentarem justificativa formal por escrito para a ausência na P1 ou na P2.

Janelas de envio de resoluções das listas de exercícios:

Listas 1 e 2 – 00h00 de sexta-feira, 1.7 às 23h59 de domingo, 3.7;
Listas 3 e 4 – 00h00 de sexta-feira, 22.7 às 23h59 de domingo, 24.7;
Listas 5 e 6 – 00h00 de sexta-feira, 5.8 às 23h59 de domingo, 7.8;
Lista 7 – 00h00 de sábado, 27.8 às 23h59 de segunda-feira, 29.8.

Durante cada janela de envio de resoluções de listas de exercícios, será aberta uma tarefa no Moodle com essa finalidade. Os detalhes sobre o envio das resoluções e as seleções de exercícios a serem resolvidos serão divulgados no início de cada janela.

Listas de exercícios

É extremamente importante que os alunos façam todas as listas, de preferência à medida que a matéria vai sendo dada, para consolidar o aprendizado do conteúdo e ver quais dúvidas aparecem. Não deixe suas dúvidas se acumularem! Pergunte!

Monitoria, atendimento online e plantão de dúvidas

Haverá um plantão de dúvidas em videoconferência às terças-feiras das 18h00 às 21h00, usando a plataforma Google Meet, tal como a transmissão síncrona das aulas.

O plantão terá início em 7.6 – por razões de segurança, o link para a sala de reunião será divulgado por email e pelo Moodle no máximo 30 minutos antes do início de cada reunião.

Tal como na transmissão síncrona das aulas, a entrada nas salas de reunião dos plantões só será permitida mediante o uso da conta Google vinculada ao email institucional da UFABC, para fins de controle da participação dos alunos.

Horários dos plantões de monitoria(início: 7.6), monitora – Wanessa Ferreira (os links para as respectivas salas de reunião no Google Meet seguem abaixo):

Controle de frequência

A frequência será controlada mediante a participação nas aulas síncronas e nos plantões de dúvidas, bem como pela entrega das resoluções das seleções de exercícios das listas. A contabilização de presença nas transmissões síncronas das aulas será semanal – basta que o aluno compareça a uma aula síncrona da semana para que sua presença nas aulas daquela semana seja computada. Observo que, em virtude do caráter remoto das aulas, o controle de frequência não será usado para fins de reprovação por falta.

Roteiro

Seguiremos de maneira aproximada o cronograma sugerido para o curso de AlgLin pelo Gradmat, com algumas modificações na ordem e na ênfase – para uma descrição mais detalhada dos tópicos de cada aula, confira a lista das aulas acima. Uma descrição sucinta dos tópicos do curso na ordem a ser seguida pode ser vista abaixo.

Espaços vetoriais: motivação, definição e exemplos (Anton-Rorres: seção 5.1; Apostol: seções 1.1 a 1.5; notas do Pellegrini: seção 1.4).
Subespaços vetoriais: definição e exemplos (Anton-Rorres: seção 5.2; Apostol: seção 1.6; notas do Pellegrini: seção 1.5).
Combinações lineares, dependência linear e independência linear. Subespaços vetoriais gerados por um conjunto de vetores (Anton-Rorres: seções 5.2 e 5.3; Apostol: seções 1.6 e 1.7; notas do Pellegrini: seção 2.1).
Bases e dimensão de um (sub)espaço vetorial, componentes de um vetor numa base. Mudança de base (Anton-Rorres: seção 5.4; Apostol: seções 1.8 a 1.10; notas do Pellegrini: seções 2.2 e 2.4).
Produtos escalares: definição e propriedades. Geometria do produto escalar: a desigualdade de Cauchy-Schwarz.
Projeções ortogonais, bases ortogonais e ortonormais. Ortonormalização de Gram-Schmidt.
Transformações lineares: definição e exemplos. A adjunta de uma transformação linear com respeito a um produto escalar.
A matriz de uma transformação linear numa base. O efeito da mudança de base na matriz de uma transformação linear, matrizes de mudança de base.
Núcleo e imagem de uma transformação linear. Posto e nulidade.
Sistemas lineares, transformações lineares e matrizes. Operações elementares e escalonamento de matrizes: algoritmos de eliminação Gaussiana e de Gauss-Jordan.
O determinante de uma transformação linear e de uma matriz.
Autovalores e autovetores: definição e interpretação geométrica. O polinômio característico.
Bases de autovetores e diagonalização de transformações lineares.
Tópicos suplementares (a serem administrados ao longo do curso se houver tempo): a pseudoinversa de uma transformação linear e decomposição em valores singulares, aplicações (regressão linear, análise de componentes principais).